Контрольные вопросы.

1. Каковы общие требования безопасности при проведении лабораторных работ по биофизике?

2. Каковы общие правила безопасности при работе с химическими веществами?

3. Правила безопасности при работе с центрифугами.

4. Каковы основные типы поражения электрическим током?

5. Какова зависимость действия тока от его величины?

6. Какие органы критичны по отношению к действию электрическим током?

7. Какие меры первой помощи оказываются пострадавшему.

Тема 1. Кинетика биологических процессов. Теоретическая часть

Все биологические процессы протекают во времени. Для описания и оценивания этого удобной количественной характеристикой является скорость реакции или скорость процесса. Знание механизмов реакций и процессов, обеспечивающих их протекание с той или иной скоростью, зависимость скорости от различных факторов (концентрации веществ, температуры, рН, наличия катализаторов-ферментов, активаторов, ингибиторов и т.д.) позволяет прогнозировать развитие реакций или процессов, оптимизировать их протекание в нужном направлении и с необходимым результатом.

Представим химическое превращение в виде простой реакции:

Скоростью этой химической реакции будет величина накопления продукта в единицу времени

;

Кинетика базируется на фундаментальном положении Гулдберга-Вааге, согласно которому скорость реакции пропорциональна произведению концентраций реагирующих веществ в степенях, соответствующих их стехиометрическим коэффициентам. Это положение, связывающее активные концентрации веществ со скоростью реакции, так же известно как закон действующих масс. В соответствие с этим законом скорость реакции может быть выражена в следующем виде:

где к – коэффициент пропорциональности, называемый константа скорости реакции.

Рассмотрим вариант простейшей реакции 1 -го порядка, когда Скорость реакции в этом случае можно выразить как

Знак минус на расходование реагента в ходе реакции.

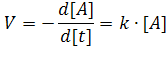
Пусть в начальный момент времени t=0 концентрация вещества А равна [А]0. После начала реакции начнется постепенное расходование реагента А и к моменту времени t = t его концентрация станет [А]. Используя эти граничные условия, проинтегрируем уравнение скоростей, предварительно разделим переменные

;

; ;

Отсюда или или ;

Из этого уравнения после потенцирования выражение для зависимости| изменения концентрации вещества от времени

При переходе к десятичным логарифмам получается ;

Отсюда определяется константа скорости 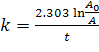, где [А]₀ и [А] - начальная и конечная концентрации вещества А.

Помимо зависимости от концентрации реагентов скорость реакции существенно зависит от температуры. Известно эмпирическое правило, называемое законом Вант-Гоффа, согласно которому при повышении температуры на 10° скорость реакции возрастает приблизительно в 2 раза. Отношение констант скоростей реакции при двух температурах, различающихся на 10°, называется температурным коэффициентом .

Правило Вант-Гоффа приближенное, поскольку температурный коэффициент Q₁₀ меняется с температурой. Более точная зависимости скорости реакции (константы скорости) от температуры выражается уравнением Аррениуса, которое учитывает кинетическую энергию реагентов, определяющих характер влияния на скорость реакции: , где А — предэкспоненциальный множитель, Т — абсолютная температура (К), R — универсальная газовая постоянная (1.98•10^-3 ккал/М•градус), Е_а - энергия активации. Она характеризует величиной энергетического потенциального барьера, который молекулы реагентов должны преодолеть для взаимодействия.

Для любого температурного интервала Q₁₀ вычисляется по формуле Вант-Гоффа: , где К₁ и К₂ константы скорости реакции при температурах t₁ и t₂ соответственно.

Очевидно при t₂ = t₁ + 10, ; (пpи )

При изучении биологических процессов вычисление К обычно затруднительно и ее заменяют непосредственно величиной скорость процесса. Энергия активации, т.е. температурная характеристика процесса выводится из уравнения Аррениуса для скорости химической реакции:

, где E_a - энергия активации.

Из уравнения следует: .

Формула устанавливает простое соотношение между Е_а и Q₁₀. Действительно, при T₂-T₁=10 и при переходе от ln к lg путем умножения на модуль 2,3 имеем: [кал/град•моль].

Энергия активации связана с температурным коэффициентом эмпирическим соотношением:

Прологарифмировав интегральное уравнение Аррениуса, получим выражение, удобное для определения величины энергии активации из экспериментально полученных величин:

Из этого выражения следует, что (или ) линейно зависит от величины обратной температуры (1/Т) (рис.1.1). Это очень удобно для графического представления кинетических экспериментальных данных. Если по оси ординат откладывать значения (или ), а по оси абсцисс -1/Т (координаты Аррениуса), то из наклона этого графика легко определяется величина энергии активации Е_а.

отсюда ;

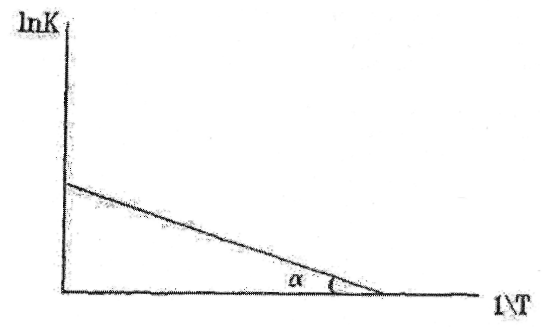
Рис. 1.1. Диаграмма Аррениуса (представление экспериментальных данных в координатах Аррениуса).

Наиболее точно зависимость константы скорости реакции от температуры определяется на основе теории абсолютных скоростей реакций Эйринга. Эта зависимость выражается уравнением Эйринга:

, где к₀ - постоянная Больцмана 1.88*10-23 Дж/К; h - постоянная Планка 6.625*10-34 Дж*сек; — изменение энтропии и энтальпии соответственно в результате химического превращения или процесса.

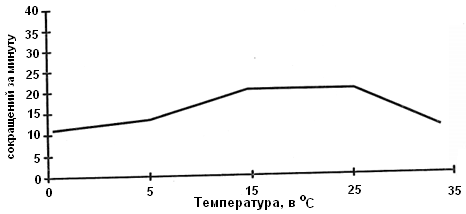
Рис. 1.2. Примерный вид зависимости ЧСС от температуры.