Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Набережночелнинский институт КФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Применение метода полного факторного эксперимен...doc

Скачиваний:

Добавлен:

09.11.2019

Размер:

636.42 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Анализ математической модели

Для удобства рассмотрения и более точной интерпретации полученных уравнений строили номограммы методом сечений поверхностей отклика у факторными плоскостями.

Расчет данных для построения номограмм производили с использованием интерполяционного приема и выполнили на ЭВМ с выдачей результатов в виде таблиц на ленту ЦПУ.

При этом уравнение (4.11) представляли в виде:

(4.20)

и просчитывали все значения х, при значениях:

х₂ от -1 до +1 с шaгoм = 0,2;

у от 50 до 200 с шагом 10

х₃ от -1 до +1 с шагом 1.

точно также решали уравнение (4.19) относительно х₂ и х_3.

Пример графической интерпретации математической модели в виде номограмм представлены на рис. 4.1.

5. Контрольные вопросы

Какие достоинства имеет математические методы планирования эксперимента?
Изложите суть метода полного факторного эксперимента.
Какие задачи можно решать методом полного факторного эксперимента?
Что такое факторы и функция отклика?
Что такое интервалы варьирования факторов и как они определяются?
Что такое факторное пространство и поверхность отклика?
Что такое матрица планирования эксперимента?
В чем состоит отличие натуральных переменных от кодированных?
Что такое уравнение регрессии?
Как проводится статистический анализ уравнения регрессии?
Как осуществляется анализ математической модели?

Литература

Вознесенский В.А., и др. Современные методы оптимизации композиционных материалов. - Киев: Будивильник, 1963-232 с.
Адлер Ю.П. Маркова Е.Б., Грамовений Ю.Б. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976- 279 с.
Адлер Ш.П. Введение в планирование эксперимента.- М.: Металлургия» 1989-157 с.
Задгинидзе М.Г. Математической планирование эксперимента для исследования и оптимизации свойств смесей.- Тбилиси: Мецнигереба, 1971-151 с.
Спиридонов A.А., Планирование эксперимента при исследовании технологических процессов. Изд-во Машиностроение. -М., 1981.

Приложение 1

Значения критерия Кохрена (F=0,95)

	1	2	3	4	5	6	7	8
2	0,999	0,975	0,939	0,906	0,877	0,853	0,833	0,816
3	0,967	0,871	0,798	0,746	0,707	0,677	0,653	0,633
4	0,907	0,768	0,684	0,629	0,590	0,560	0,637	0,518
5	0,841	0,684	0,598	0,544	0,507	0,478	0,456	0,439
6	0,781	0,616	0,532	0,480	0,445	0,418	0,398	0,382
7	0,727	0,561	0,480	0,431	0,397	0,373	0,354	0,338
8	0,680	0,516	0,438	0,391	0,360	0,336	0,319	0,304
9	0,639	0,478	0,403	0,358	0,329	0,307	0,290	0,277
10	0,602	0,445	0,373	0,331	0,303	0,282	0,267	0,254
12	0,541	0,392	0,326	0,288	0,262	0,244	0,230	0,219
15	0,471	0,335	0,276	0,242	0,220	0,203	0,191	0,182

Приложение 2

Значения критерия Стьюдента (Р=0,95)

1	12,71	11	2,20
2	4,30	12	2,18
3	3,18	13	2,16
4	2,78	14	2,14
5	2,57	15	2,13
6	2,45	16	2,12
7	2,36	17	2,11
8	2,31	18	2,10
9	2,26	19	2,09
10	2,23	20	2,09

Приложение 3

Таблица случайных чисел

56	66	25	32	38	64	70	26	27	67	77	40	04	34	63	98	99	89	31	16	12	90	50	28
88	40	52	02	29	82	69	34	50	21	74	00	91	27	52	98	72	03	45	65	30	89	71	45
87	63	88	23	62	51	07	69	59	02	89	49	14	98	53	41	92	36	07	76	85	37	84	37
32	25	21	15	08	82	34	57	57	35	22	03	33	48	83	37	37	29	38	37	89	76	25	09
44	61	88	23	13	01	59	47	64	04	99	59	96	20	30	87	31	33	69	45	58	48	00	83
94	44	08	67	79	41	61	41	15	60	11	88	83	24	82	24	07	78	61	89	42	58	88	22
13	24	40	09	00	65	46	38	61	12	90	62	41	11	59	85	18	42	61	29	88	76	04	21
78	27	84	05	99	85	75	67	80	05	57	05	71	70	21	31	99	99	06	96	53	99	25	13
42	39	30	02	34	99	46	68	45	15	19	74	15	50	17	44	80	13	86	38	40	45	82	13
04	52	43	96	38	13	83	80	72	34	20	84	56	19	49	59	14	85	42	99	71	16	34	33
82	85	77	30	16	69	32	46	46	30	84	20	68	72	98	54	62	63	59	44	00	89	06	15
38	48	84	88	24	55	46	48	60	06	90	08	83	83	98	40	90	88	25	26	85	74	55	80
91	19	05	68	22	58	04	63	21	16	23	38	25	43	32	98	94	65	35	35	16	91	07	12
54	81	87	21	31	40	46	17	62	63	99	71	14	12	64	51	68	50	60	78	22	69	51	98
65	43	75	12	91	20	36	25	57	92	33	65	95	48	75	00	06	65	25	90	16	29	34	14
49	98	71	31	80	59	57	32	43	07	85	06	64	75	27	29	17	06	11	30	68	70	97	87
03	98	68	89	39	71	87	32	14	99	42	10	25	37	30	08	27	75	43	97	54	20	69	93
56	04	21	34	92	89	81	52	15	12	84	11	12	66	87	47	21	06	86	08	35	39	52	28
48	09	36	95	36	20	82	53	32	89	92	68	50	88	17	37	92	02	23	43	65	24	69	80
23	97	10	96	57	74	07	95	26	44	93	08	43	30	41	86	45	74	33	78	84	33	38	76
43	97	55	45	98	35	69	45	96	80	46	26	39	96	33	60	20	73	30	79	17	19	03	47
40	05	08	50	79	89	58	19	86	48	27	98	99	24	08	94	17	15	81	29	82	14	35	88
66	97	10	69	02	25	36	43	71	76	00	67	56	12	69	7	89	55	63	31	50	72	20	33
15	62	38	72	92	03	76	09	30	75	77	80	04	24	59	67	60	10	79	26	21	60	03	48
77	81	15	14	67	55	24	22	20	55	36	93	67	69	37	72	22	43	46	32	56	15	75	25
18	87	05	09	96	45	14	72	41	46	12	67	46	72	02	59	06	17	49	12	73	28	23	52
08	58	53	63	96	13	07	04	48	71	39	07	46	96	40	20	86	79	11	81	74	11	15	23
16	07	79	57	61	42	19	68	15	12	60	21	59	12	07	04	99	88	22	39	75	16	69	13

Приложение 4

Число степеней свободы	Число степеней свободы (для числителя)
Число степеней свободы	1	2	3	4	5	6	7	8
1	161,45	199,50	215,71	224,16	230,16	233,99	236,77	238,88
2	18,51	19,00	19,16	19,25	19,30	19,33	19,35	19,37
3	10,13	9,55	9,28	9,12	9,01	8,94	8,89	8,85
4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73
8	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44
9	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,24
10	4,97	4,10	3,71	3,48	3,33	3,22	3,14	3,07
11	4,84	3,98	3,59	3,36	3,20	3,10	3,01	2,95
12	4,75	3,89	3,49	3,26	3,11	3,00	2,91	2,85
13	4,67	3,81	3,41	3,18	3,03	2,92	2,83	2,77
14	4,60	3,74	3,34	3,11	2,96	2,85	2,76	2,70
15	4,54	3,68	3,29	3,06	2,90	2,79	2,71	2,64
16	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59
17	4,45	3,59	3,20	2,97	2,81	2,70	2,71	2,55
18	4,41	3,56	3,16	2,93	2,77	2,66	2,58	2,51
19	4,38	3,52	3,13	2,90	2,74	2,63	2,54	2,48
20	4,35	3,49	3,10	2,87	2,71	2,60	2,51	2,45

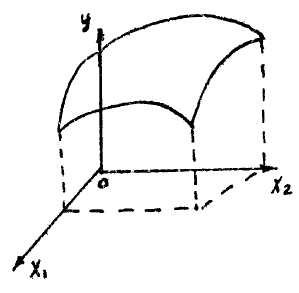
Рис.2.1. Поверхность отклика Рис. 2.2. Сечение функции

отклика факторными плоскостями

Рис. 3.1 Переход к кодированным переменным

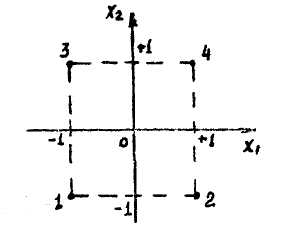
Рис. 3.2. Построение опытов полдвухфакторного эксперимента

Рис 3.3. Построение опытов полного трёхфакторного эксперимента

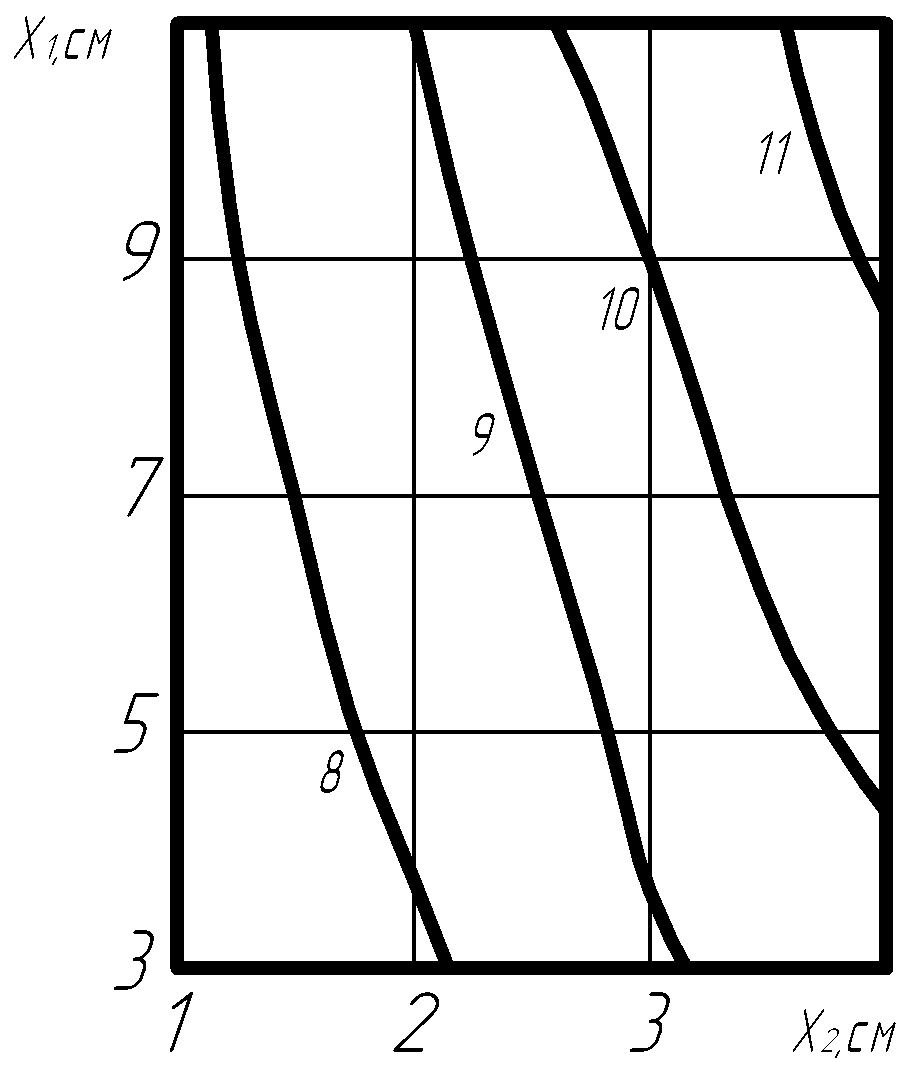
а) б) в)

Рис. 4.1. Изолинии твёрдости упрочнённых материалов в зависимости: силы тока дуги – х₁(A) от расстояния обработки материала х₂(см); при времени обработки (х₃)

равном а) 0,4; б) 0,5; в) 0,6

_____________________________________________

Подписано в печать 2.02.12 г.

Формат Бумага офсетная Печать ризографическая

Уч.-изд.л 2.0 Усл.-печ.л. 2.0 тираж 50 экз.

Заказ 1635

Издательско-полиграфический центр

Камской государственной инженерно-экономической академии

_________________________________________________

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.11.2018814.59 Кб1ПРАКТИКА стратег.doc
#
26.02.2016454.66 Кб36практикум по финансовому праву (16 тем).doc
#
21.11.2018610.3 Кб4Предмет философии(1).doc
#
01.05.202584.48 Кб0Предупреждение преступлений.doc
#
26.02.201615.6 Mб25применение композитной арматуры в бетонных конструкциях (бенмокрэйн).pdf
#
09.11.2019636.42 Кб9Применение метода полного факторного эксперимен...doc
#
01.04.202598.82 Кб3пример выполнения РГР спец 19060165 08г.doc
#
09.11.2019432.13 Кб5пример выполненной контрольной работы.doc
#
05.12.2018730.11 Кб7пример курсовой работы.doc
#
01.04.2025123.9 Кб0Принципы, функции и методы менеджмента..doc
#
26.02.2016181.25 Кб29Пробл_Logica.doc

56	66	25	32	38	64	70	26	27	67	77	40	04	34	63	98	99	89	31	16	12	90	50	28
88	40	52	02	29	82	69	34	50	21	74	00	91	27	52	98	72	03	45	65	30	89	71	45
87	63	88	23	62	51	07	69	59	02	89	49	14	98	53	41	92	36	07	76	85	37	84	37
32	25	21	15	08	82	34	57	57	35	22	03	33	48	83	37	37	29	38	37	89	76	25	09
44	61	88	23	13	01	59	47	64	04	99	59	96	20	30	87	31	33	69	45	58	48	00	83
94	44	08	67	79	41	61	41	15	60	11	88	83	24	82	24	07	78	61	89	42	58	88	22
13	24	40	09	00	65	46	38	61	12	90	62	41	11	59	85	18	42	61	29	88	76	04	21
78	27	84	05	99	85	75	67	80	05	57	05	71	70	21	31	99	99	06	96	53	99	25	13
42	39	30	02	34	99	46	68	45	15	19	74	15	50	17	44	80	13	86	38	40	45	82	13
04	52	43	96	38	13	83	80	72	34	20	84	56	19	49	59	14	85	42	99	71	16	34	33
82	85	77	30	16	69	32	46	46	30	84	20	68	72	98	54	62	63	59	44	00	89	06	15
38	48	84	88	24	55	46	48	60	06	90	08	83	83	98	40	90	88	25	26	85	74	55	80
91	19	05	68	22	58	04	63	21	16	23	38	25	43	32	98	94	65	35	35	16	91	07	12
54	81	87	21	31	40	46	17	62	63	99	71	14	12	64	51	68	50	60	78	22	69	51	98
65	43	75	12	91	20	36	25	57	92	33	65	95	48	75	00	06	65	25	90	16	29	34	14
49	98	71	31	80	59	57	32	43	07	85	06	64	75	27	29	17	06	11	30	68	70	97	87
03	98	68	89	39	71	87	32	14	99	42	10	25	37	30	08	27	75	43	97	54	20	69	93
56	04	21	34	92	89	81	52	15	12	84	11	12	66	87	47	21	06	86	08	35	39	52	28
48	09	36	95	36	20	82	53	32	89	92	68	50	88	17	37	92	02	23	43	65	24	69	80
23	97	10	96	57	74	07	95	26	44	93	08	43	30	41	86	45	74	33	78	84	33	38	76
43	97	55	45	98	35	69	45	96	80	46	26	39	96	33	60	20	73	30	79	17	19	03	47
40	05	08	50	79	89	58	19	86	48	27	98	99	24	08	94	17	15	81	29	82	14	35	88
66	97	10	69	02	25	36	43	71	76	00	67	56	12	69	7	89	55	63	31	50	72	20	33
15	62	38	72	92	03	76	09	30	75	77	80	04	24	59	67	60	10	79	26	21	60	03	48
77	81	15	14	67	55	24	22	20	55	36	93	67	69	37	72	22	43	46	32	56	15	75	25
18	87	05	09	96	45	14	72	41	46	12	67	46	72	02	59	06	17	49	12	73	28	23	52
08	58	53	63	96	13	07	04	48	71	39	07	46	96	40	20	86	79	11	81	74	11	15	23
16	07	79	57	61	42	19	68	15	12	60	21	59	12	07	04	99	88	22	39	75	16	69	13

56	66	25	32	38	64	70	26	27	67	77	40	04	34	63	98	99	89	31	16	12	90	50	28
88	40	52	02	29	82	69	34	50	21	74	00	91	27	52	98	72	03	45	65	30	89	71	45
87	63	88	23	62	51	07	69	59	02	89	49	14	98	53	41	92	36	07	76	85	37	84	37
32	25	21	15	08	82	34	57	57	35	22	03	33	48	83	37	37	29	38	37	89	76	25	09
44	61	88	23	13	01	59	47	64	04	99	59	96	20	30	87	31	33	69	45	58	48	00	83
94	44	08	67	79	41	61	41	15	60	11	88	83	24	82	24	07	78	61	89	42	58	88	22
13	24	40	09	00	65	46	38	61	12	90	62	41	11	59	85	18	42	61	29	88	76	04	21
78	27	84	05	99	85	75	67	80	05	57	05	71	70	21	31	99	99	06	96	53	99	25	13
42	39	30	02	34	99	46	68	45	15	19	74	15	50	17	44	80	13	86	38	40	45	82	13
04	52	43	96	38	13	83	80	72	34	20	84	56	19	49	59	14	85	42	99	71	16	34	33
82	85	77	30	16	69	32	46	46	30	84	20	68	72	98	54	62	63	59	44	00	89	06	15
38	48	84	88	24	55	46	48	60	06	90	08	83	83	98	40	90	88	25	26	85	74	55	80
91	19	05	68	22	58	04	63	21	16	23	38	25	43	32	98	94	65	35	35	16	91	07	12
54	81	87	21	31	40	46	17	62	63	99	71	14	12	64	51	68	50	60	78	22	69	51	98
65	43	75	12	91	20	36	25	57	92	33	65	95	48	75	00	06	65	25	90	16	29	34	14
49	98	71	31	80	59	57	32	43	07	85	06	64	75	27	29	17	06	11	30	68	70	97	87
03	98	68	89	39	71	87	32	14	99	42	10	25	37	30	08	27	75	43	97	54	20	69	93
56	04	21	34	92	89	81	52	15	12	84	11	12	66	87	47	21	06	86	08	35	39	52	28
48	09	36	95	36	20	82	53	32	89	92	68	50	88	17	37	92	02	23	43	65	24	69	80
23	97	10	96	57	74	07	95	26	44	93	08	43	30	41	86	45	74	33	78	84	33	38	76
43	97	55	45	98	35	69	45	96	80	46	26	39	96	33	60	20	73	30	79	17	19	03	47
40	05	08	50	79	89	58	19	86	48	27	98	99	24	08	94	17	15	81	29	82	14	35	88
66	97	10	69	02	25	36	43	71	76	00	67	56	12	69	7	89	55	63	31	50	72	20	33
15	62	38	72	92	03	76	09	30	75	77	80	04	24	59	67	60	10	79	26	21	60	03	48
77	81	15	14	67	55	24	22	20	55	36	93	67	69	37	72	22	43	46	32	56	15	75	25
18	87	05	09	96	45	14	72	41	46	12	67	46	72	02	59	06	17	49	12	73	28	23	52
08	58	53	63	96	13	07	04	48	71	39	07	46	96	40	20	86	79	11	81	74	11	15	23
16	07	79	57	61	42	19	68	15	12	60	21	59	12	07	04	99	88	22	39	75	16	69	13

56	66	25	32	38	64	70	26	27	67	77	40	04	34	63	98	99	89	31	16	12	90	50	28
88	40	52	02	29	82	69	34	50	21	74	00	91	27	52	98	72	03	45	65	30	89	71	45
87	63	88	23	62	51	07	69	59	02	89	49	14	98	53	41	92	36	07	76	85	37	84	37
32	25	21	15	08	82	34	57	57	35	22	03	33	48	83	37	37	29	38	37	89	76	25	09
44	61	88	23	13	01	59	47	64	04	99	59	96	20	30	87	31	33	69	45	58	48	00	83
94	44	08	67	79	41	61	41	15	60	11	88	83	24	82	24	07	78	61	89	42	58	88	22
13	24	40	09	00	65	46	38	61	12	90	62	41	11	59	85	18	42	61	29	88	76	04	21
78	27	84	05	99	85	75	67	80	05	57	05	71	70	21	31	99	99	06	96	53	99	25	13
42	39	30	02	34	99	46	68	45	15	19	74	15	50	17	44	80	13	86	38	40	45	82	13
04	52	43	96	38	13	83	80	72	34	20	84	56	19	49	59	14	85	42	99	71	16	34	33
82	85	77	30	16	69	32	46	46	30	84	20	68	72	98	54	62	63	59	44	00	89	06	15
38	48	84	88	24	55	46	48	60	06	90	08	83	83	98	40	90	88	25	26	85	74	55	80
91	19	05	68	22	58	04	63	21	16	23	38	25	43	32	98	94	65	35	35	16	91	07	12
54	81	87	21	31	40	46	17	62	63	99	71	14	12	64	51	68	50	60	78	22	69	51	98
65	43	75	12	91	20	36	25	57	92	33	65	95	48	75	00	06	65	25	90	16	29	34	14
49	98	71	31	80	59	57	32	43	07	85	06	64	75	27	29	17	06	11	30	68	70	97	87
03	98	68	89	39	71	87	32	14	99	42	10	25	37	30	08	27	75	43	97	54	20	69	93
56	04	21	34	92	89	81	52	15	12	84	11	12	66	87	47	21	06	86	08	35	39	52	28
48	09	36	95	36	20	82	53	32	89	92	68	50	88	17	37	92	02	23	43	65	24	69	80
23	97	10	96	57	74	07	95	26	44	93	08	43	30	41	86	45	74	33	78	84	33	38	76
43	97	55	45	98	35	69	45	96	80	46	26	39	96	33	60	20	73	30	79	17	19	03	47
40	05	08	50	79	89	58	19	86	48	27	98	99	24	08	94	17	15	81	29	82	14	35	88
66	97	10	69	02	25	36	43	71	76	00	67	56	12	69	7	89	55	63	31	50	72	20	33
15	62	38	72	92	03	76	09	30	75	77	80	04	24	59	67	60	10	79	26	21	60	03	48
77	81	15	14	67	55	24	22	20	55	36	93	67	69	37	72	22	43	46	32	56	15	75	25
18	87	05	09	96	45	14	72	41	46	12	67	46	72	02	59	06	17	49	12	73	28	23	52
08	58	53	63	96	13	07	04	48	71	39	07	46	96	40	20	86	79	11	81	74	11	15	23
16	07	79	57	61	42	19	68	15	12	60	21	59	12	07	04	99	88	22	39	75	16	69	13