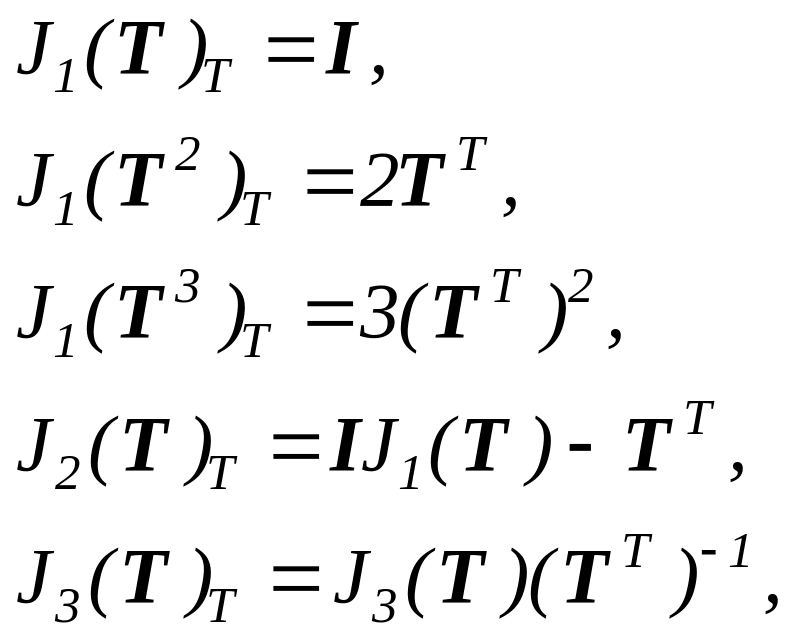4.3. Производная тензорной функции
Для определения
производной функции (сначала скалярозначной)
тензорного аргумента сначала сведем
последнюю к функции нескольких скалярных
переменных

 (4.3.1)
(4.3.1)
путем отнесения
тензора-аргумента к произвольному
ортобазису. Разлагаем (4.3.1) в степенной
ряд
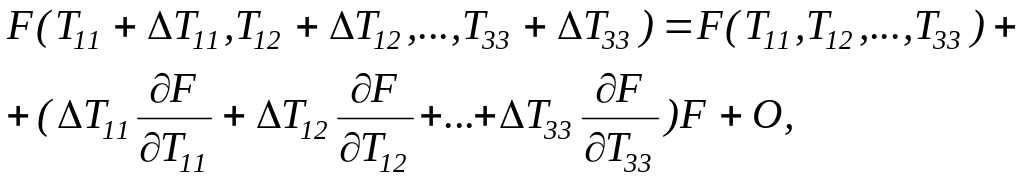 (4.3.2)
(4.3.2)
где
 обозначает члены более высокого порядка
малости относительно
обозначает члены более высокого порядка
малости относительно
 .
Выражение (4.3.2) можно кратко записать в
более привычном виде
.
Выражение (4.3.2) можно кратко записать в
более привычном виде
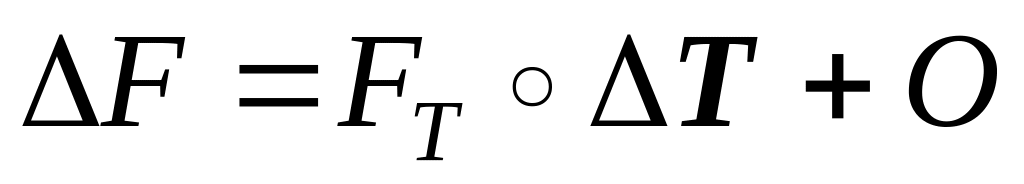 , (4.3.3)
, (4.3.3)
где 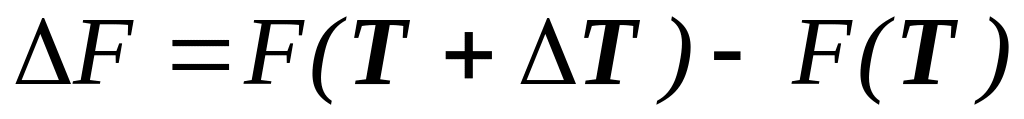 ,
,
 ,
,
а тензор второго
ранга
 (4.3.4)
(4.3.4)
и есть производная
функции
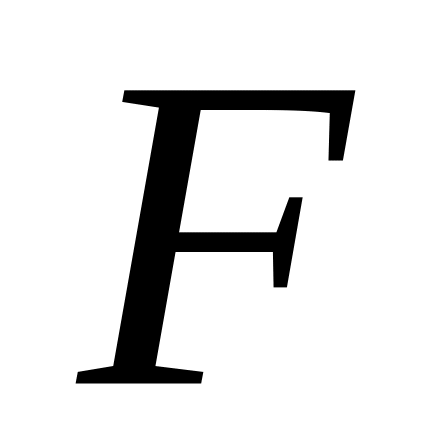 по
.
Для ее нахождения согласно (4.3.4) необходимо
отыскать частные производные
по всем компонентам
по
.
Для ее нахождения согласно (4.3.4) необходимо
отыскать частные производные
по всем компонентам
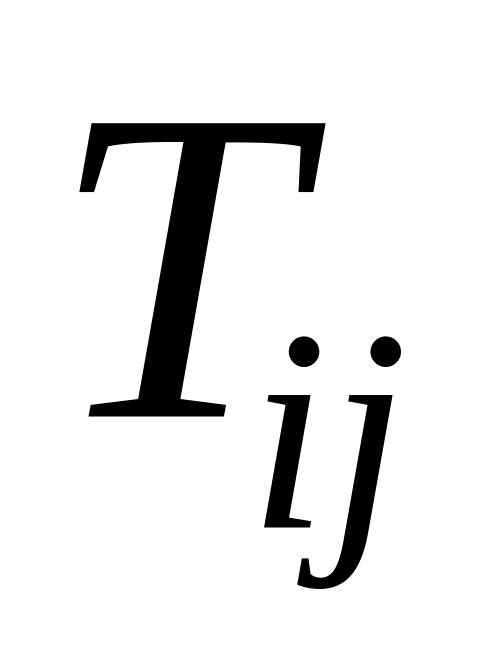 и свернуть их с исходным базисом.
и свернуть их с исходным базисом.
Разложение (4.3.3)
в пределе
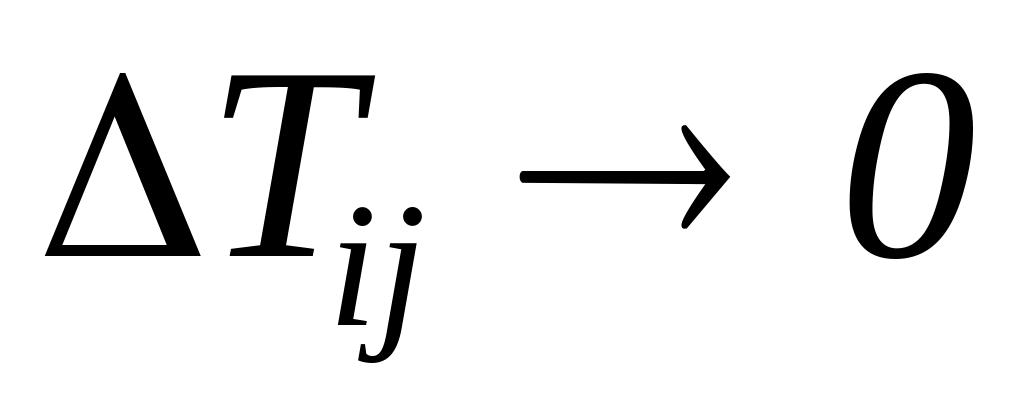 принимает вид
принимает вид
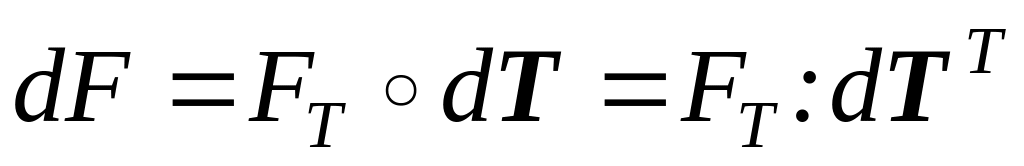 . (4.3.5)
. (4.3.5)
Это выражение
можно использовать для бескомпонентного
нахождения производной тензорной
функции. Для этого в выражении дифференциала
функции необходимо выделить
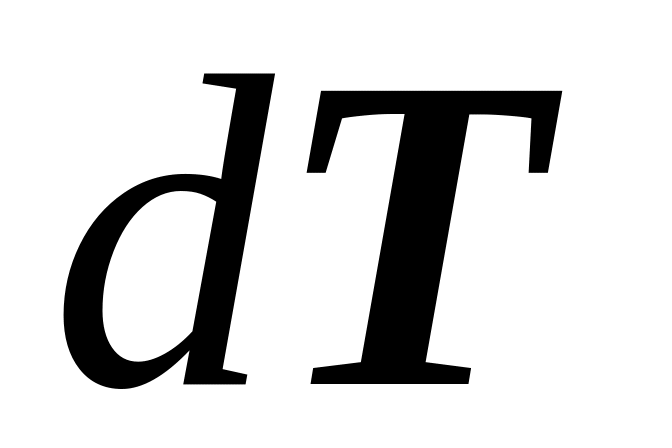 .
.
Пусть,
например,
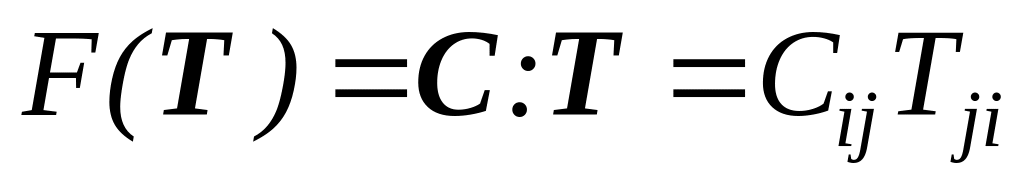 .
Тогда
.
Тогда
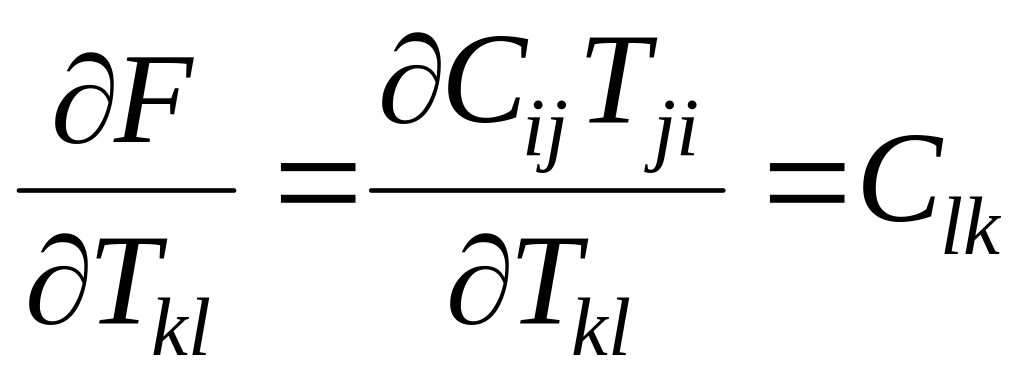 и
и
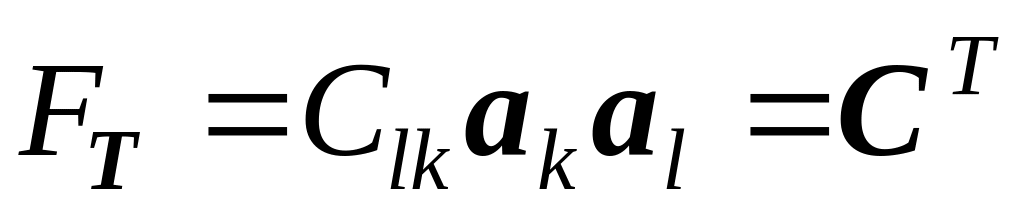 .
Другим способом:
.
Другим способом:
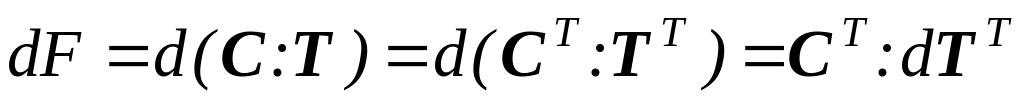 и
и
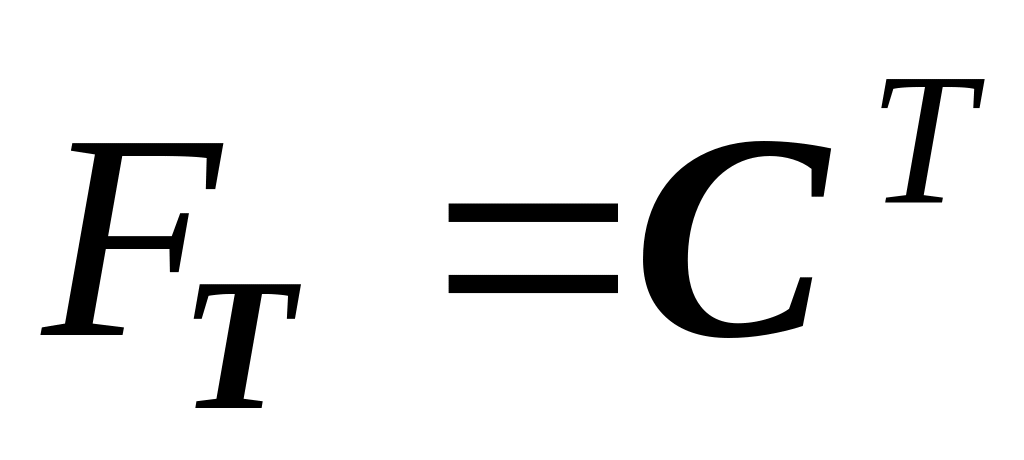 .
.
При компонентном
нахождении производной возникает задача
записи результата в бескомпонентном
виде (ведь исходная функция дается
именно в таком виде).
Бескомпонентным
способом удобнее находить
производную,
если доказать правила дифференцирования
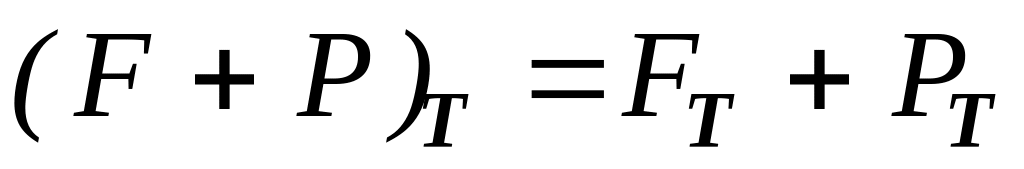 ,
,
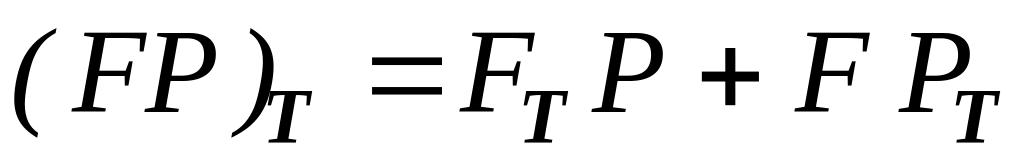 ,
,
 ,
,
 ,
,
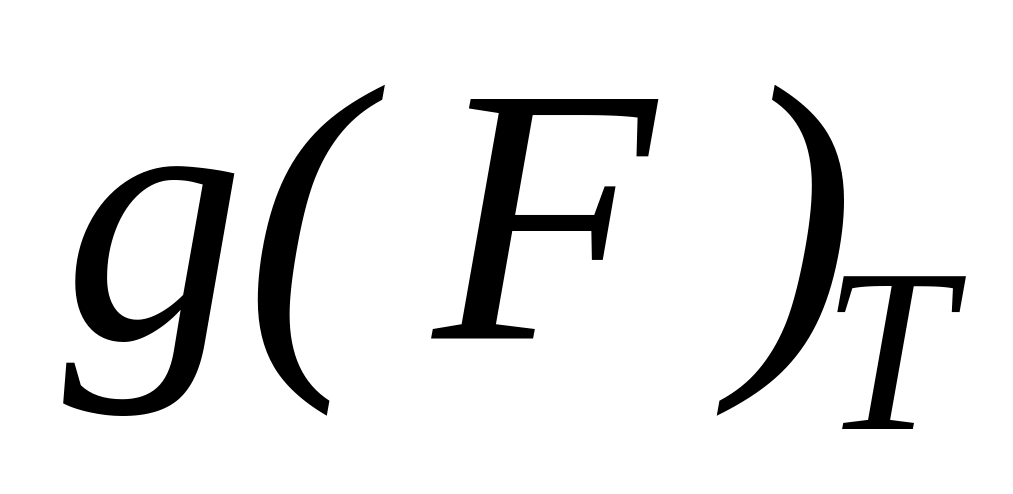
(
и
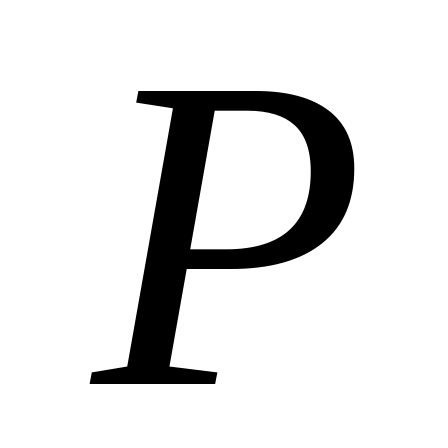 — функции
),
что предлагается сделать читателю.
— функции
),
что предлагается сделать читателю.
Читателю предлагается
также доказать
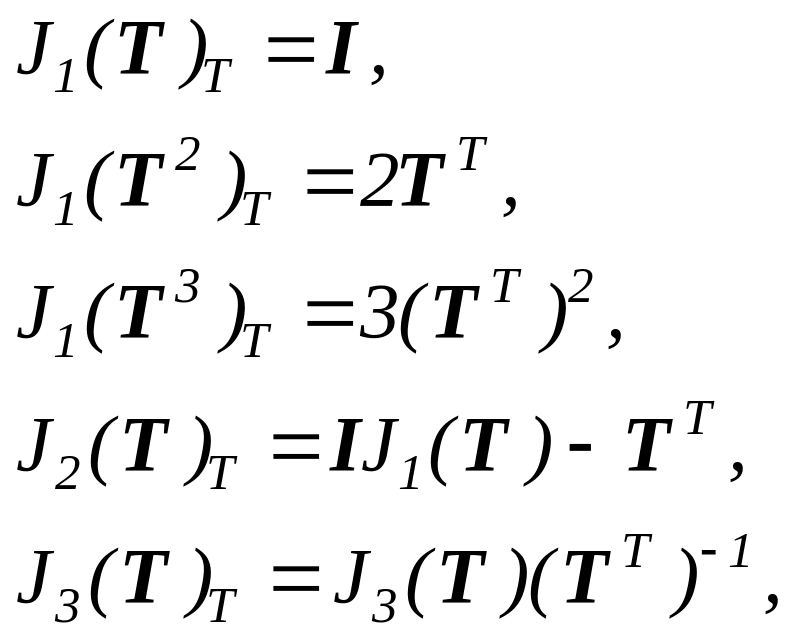
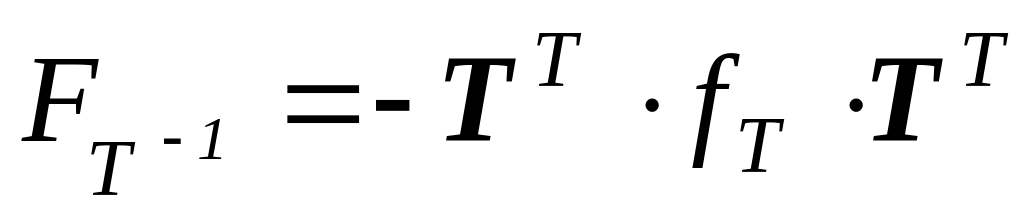
и найти производные
по
следующих функций:
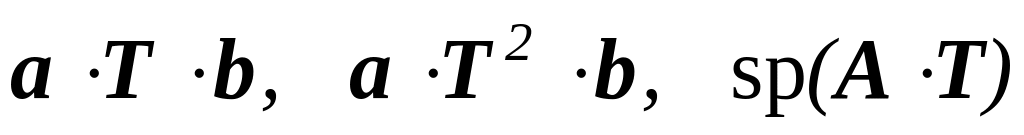 .
.
Аналогичным
способом можно вывести выражение для
производной тензорзначной функции
тензорного аргумента:
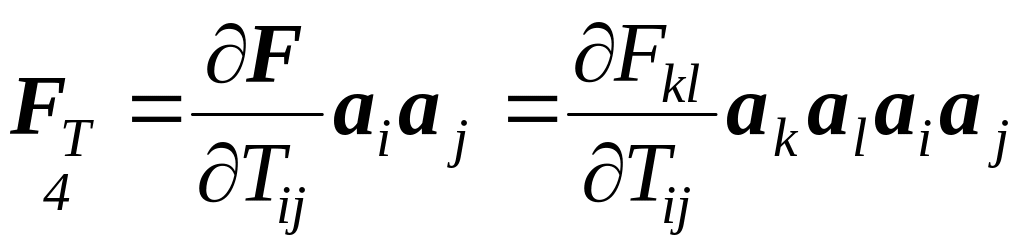 (4.3.6)
(4.3.6)
(которая есть
тензор IV
ранга) или в бескомпонентном виде
 . (4.3.7)
. (4.3.7)
С помощью данных
определений можно доказать правила для
бескомпонентного нахождения производной
тензорзначных функций
 ,
,
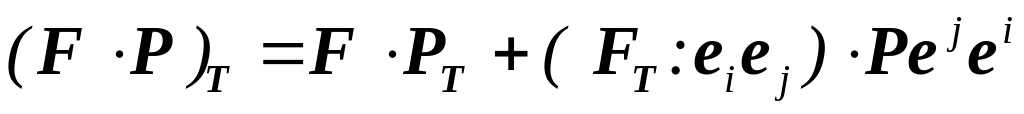 .
.
Найдите производные
следующих тензорзначных функций
:
,
,
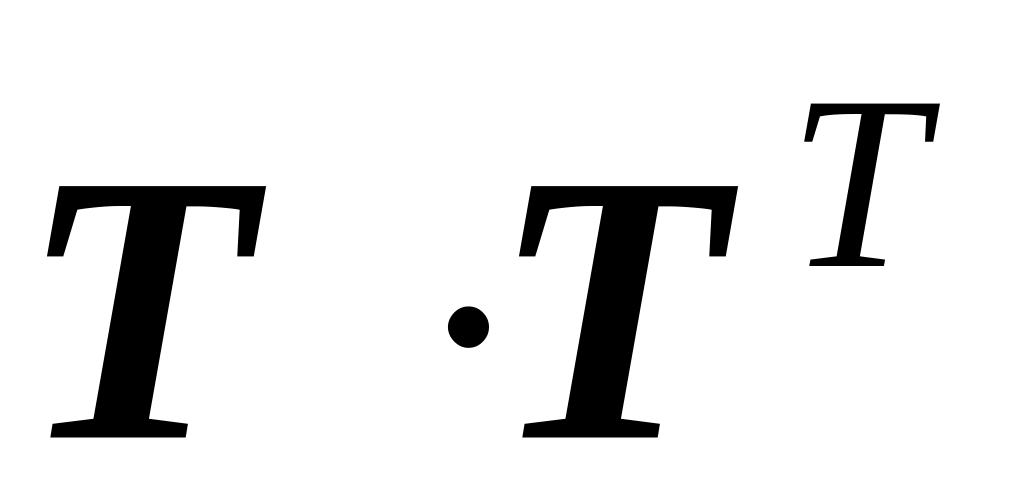 ,
,
 ,
,
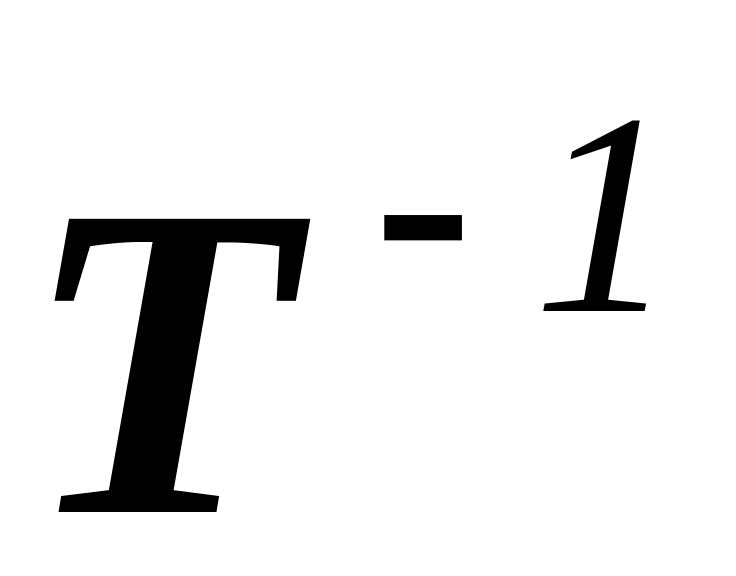 .
.
Найдите также
вторую производную второго и третьего
инвариантов.


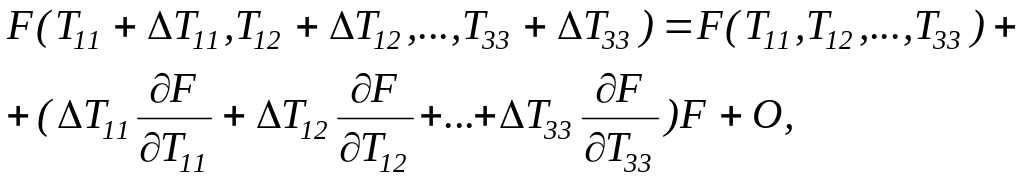 (4.3.2)
(4.3.2)