Лабораторна робота №3 Чисельне обчислення інтегралів в одновимірному випадку з використанням ізопараметричних координат
Звичайно, при створенні програмного забезпечення для розв’язування прикладних задач методом скінченних елементів мало використовують обчислення інтегралів від базисних функцій «вручну». Тому постає необхідність в чисельному обчисленні таких інтегралів. Враховуючи, що базисні функції МСЕ – це поліноми певного степеня, найбільш зручними для використання та точності є квадратурні формули Гауса [4].
Як ми побачили в попередніх лабораторних роботах
,
де
‑ деяка функція, визначена на
,
а
‑ відображення згідно (Л1.2).
Далі, згідно квадратурних формул,
маємо
,
де
‑ так звані квадратурні коефіцієнти,
‑ вузли інтегрування.
Нижче наведено
значення квадратурних коефіцієнтів та
вузлів інтегрування згідно квадратурних
формул Гауса при
та
[4] (точність формул
визначається степенем
).
|
|
|
0 |
0 |
0,0625 |
1 |
0,212340538 |
0,328844320 |
2 |
0,590533136 |
0,388193469 |
3 |
0,911412040 |
0,220462211 |
|
|
|
0 |
0 |
0,04 |
1 |
0,139759864 |
0,223103901 |
2 |
0,416409568 |
0,311826523 |
3 |
0,723156986 |
0,281356015 |
4 |
0,942895804 |
0,143713561 |
|
|
|
0 |
0 |
0,027777778 |
1 |
0,0985350860 |
0,159820377 |
2 |
0,304535727 |
0,242693594 |
3 |
0,562025190 |
0,260463392 |
4 |
0,801986582 |
0,208450667 |
5 |
0,960190143 |
0,100794193 |
Завдання. Обчислити інтеграл чисельно з використанням квадратурних формул Гауса.
1.
,
;
2.
,
;
3.
,
;
4.
,
;
5.
,
;
6.
,
;
7.
,
;
8.
,
;
9.
,
;
10.
,
;
11.
,
;
12.
,
;
13.
,
;
14.
,
;
15.
,
;
16.
,
;
17.
,
;
18.
,
;
19.
,
;
20.
,
;
21.
,
;
22.
,
;
23.
,
;
24.
,
;
25.
,
.
Лабораторна робота №4 Метод скінчених елементів в одновимірному випадку: лінійні базисні функції
Розглянемо наступну
крайову задачу для відшукання невідомої
функції
в області
:
,
(Л4.1)
.
(Л4.2)
Позначимо через
множину функцій
,
які в області
належать простору Соболєва
і приймають нульові значення на тих
кінцях відрізка
,
де для шуканої функції
задаються граничні умови першого роду.
Тобто,
Домножимо рівняння
(Л4.1) на довільну функцію
і проінтегруємо отриману рівність по
відрізку
.
Отримаємо
(Л4.3)
До першого інтеграла у лівій частині рівності (Л4.3) застосуємо формулу інтегрування за частинами
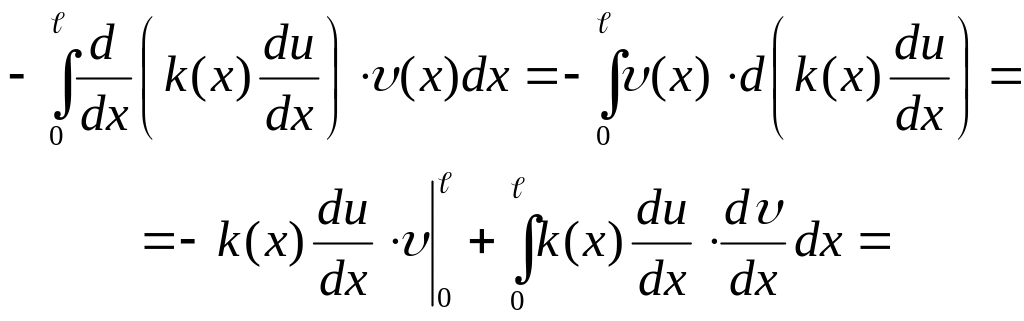
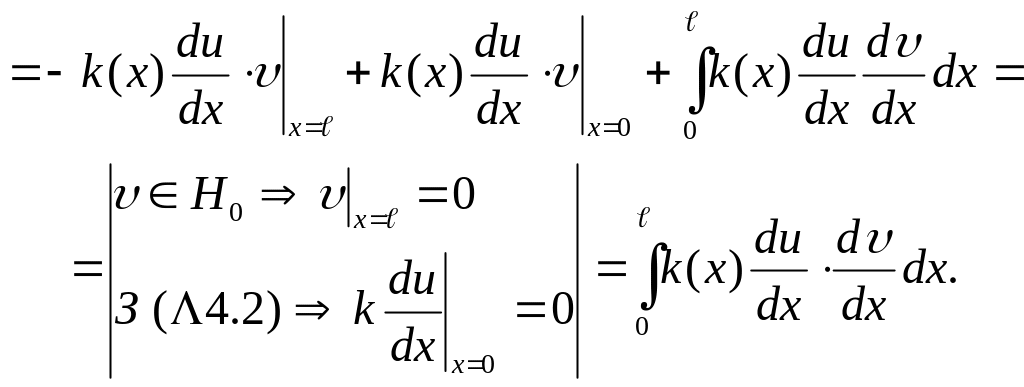
Отже, з (Л4.3) отримаємо
.
(Л4.4)
З (Л4.4) випливає,
що вимоги до функцій рівняння (Л4.1)
наступні: функція
має належати простору Соболєва
,
а функції
,
,
,
повинні бути інтегровними в області
.
Позначимо через
множину функцій, які в області
належать простору Соболєва та
задовольняють граничним умовам першого
роду з (Л4.2), що і невідома функція
Зауважимо, що оскільки в нас гранична
умова першого роду (Л4.2)
однорідна, то в даному випадку
.
Для відшукання наближеного
узагальненого розв’язку
задачі (Л4.1), (Л4.2) введемо
в розгляд скінченновимірний підпростір
простору
з базисом
.
Наближений узагальнений розв’язок
задачі (Л4.1), (Л4.2) будемо шукати у вигляді
(Л4.5)
де
‑ невідомі коефіцієнти, які потрібно
знайти.
Сукупність функцій,
які можна подати у вигляді (Л4.5) породжують
множину
В даному випадку
оскільки гранична умова першого роду
з (Л4.2) є однорідною. Розгляд просторів
,
,
,
пов’язано з тим, що метод скінченних
елементів є варіантом методу
Бубнова-Гальоркіна, який, в свою чергу,
відноситься до загального проекційного
методу [5].
Для відшукання
невідомих
,
підставимо (Л4.5) в (Л4.4) замість
,
а функцію
почергово покладаємо рівною кожній з
базисних функції
.
Отримаємо
(Л4.6)
Рівність (Л4.6) –
система лінійних алгебричних рівнянь
(СЛАР) для відшукання вектор-стовпця
невідомих
.
Дану СЛАР запишемо у матричному вигляді
(Л4.7)
де
,
,
.
В якості базисних
функцій
,
,
в (Л4.5) візьмемо кусково-лінійні базисні
функції МСЕ. Розіб’ємо відрізок
на
скінченних елементів
,
.
Визначимо базисну функцію
на всьому відрізку
,
як кусково-лінійний поліном, який
задовольняє наступним умовам (рис. 1.1):
при
Зрозуміло, що при
відсутня умова
,
а при
немає умови
.
Рис. Л4.1. Кусково-лінійні базисні функції методу скінченних елементів
Використовуючи інтерполяційну формулу Лагранжа, отримуємо
;
Побудовані функції
неперервні на
і мають розривні перші похідні, які
інтегровані з квадратом. Отже,
.
При означенні
множини
та
їх елементи-функції прив’язувались до
граничних умов першого роду для шуканої
функції
.
Тобто, вже при побудові наближеного
розв’язку (Л4.5) вимагається, щоб функція
відразу задовольняла граничним умовам
першого роду з (Л4.2). Такі
граничні умови називаються головними.
Підставляючи (Л4.5), де
,
в другу із умов (Л4.2) і враховуючи,
що
,
,
,
маємо
.
Отже, в СЛАР (Л4.7) перший рядок та
стовпець повинні бути викреслені.
При використанні
кусково–лінійних базисних функцій МСЕ
в СЛАР (Л4.7)
,
якщо
.
Тобто, матриця
буде стрічковою трьохдіагональною (в
рядку під номером
відмінними від нуля будуть елементи
,
,
).
До ансамблювання (побудови) матриці
існує два підходи:
перебираються почергово всі базисні функції і для кожної визначається її внесок в матрицю ;
перебираються всі скінченні елементи і для кожного визначається його внесок в матрицю , адже
де
‑ внесок елемента з номером
в елемент матриці
.
Алгоритм ансамблювання матриці згідно другого способу
Всі елементи матриці
покладаються рівним нулю; номер елемента
(елемент з номером
)
тоді відмінними
від нуля на елементі
будуть
;
Покладаємо
Якщо
,
то завершуємо ансамблювання; в
протилежному випадку переходимо до
пункту 2.
Зауважимо, що у випадку кусково‑лінійних базисних функцій (див. лабораторна робота №1)
;
;
;
;
.
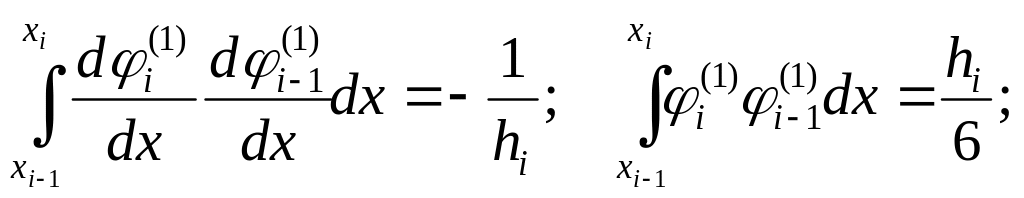
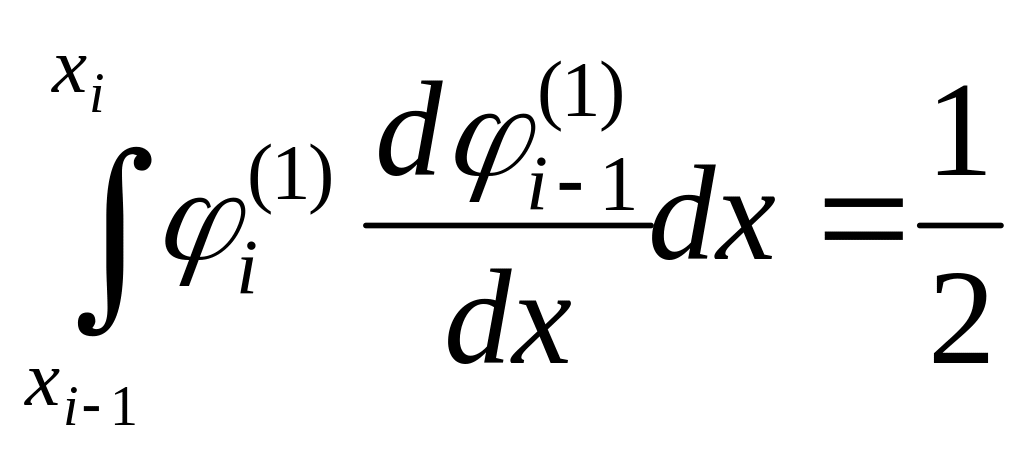Елементи
вектор‑стовпця
в СЛАР (Л4.7) формуються
аналогічним чином. Тобто
де
‑ внесок елемента з номером
.
Якщо
,
,
,
не є константами, то для визначення
внесків в матрицю
та вектор-стовпець
потрібно застосовувати формули
чисельного інтегрування (див. лабораторну
роботу №3).
Завдання. Знайти розв’язок наступної крайової задачі методом скінчених елементів з використанням кусково–лінійних базисних функцій і порівняти знайдений наближений розв’язок з точним.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
,
.
,
.
,
.
,
.
,
.