Контрольная работа по теме: "Численное дифференцирование"

Задание. Для таблично заданной функции вычислить первую и вторую производные в точке 0.8, используя простейшие формулы численного дифференцирования.

Вариант	Функция
1.		0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.2
2.		0.47943	0.56464	0.64422	0.71736	0.78333	0.84147	0.89121	0.93204
3.		0.54630	0.68414	0.84229	1.02964	1.26016	1.55741	1.96476	2.57215

Тестовые задания по теме: "Численное дифференцирование"

1.  Чем вызвана погрешность округления при вычислении производной по формулам численного дифференцирования?

а) Погрешность округления вызвана заменой данной функции f(x) интерполяционным многочленом P_n(x).

б) Погрешность округления вызвана неточным заданием начальным и граничных данных для исходной функции f(x).

в) Погрешность округления вызвана неточным заданием исходных значений данной функции f(x).

2. Назовите области применения формул численного дифференцирования.

а) К численному дифференцированию чаще всего прибегают, когда требуется определить допустимую погрешность аргументов по допустимой погрешности функции.

б) К численному дифференцированию чаще всего прибегают, когда приходится вычислять значения функции в промежуточных точках, при этом данная функция задана в табличном виде и аналитическое выражение функции неизвестно.

в) К численному дифференцированию чаще всего прибегают, когда приходится вычислять производные от функций, заданных таблично, или когда непосредственное дифференцирование функции затруднительно.

3.Найдите приближенное значение первой производной функции в точке х = 1,43 по формуле Лагранжа.

а) 5,1290

б) 6,1356

в) 12,2712

4. Чем вызвана погрешность усечения при вычислении производной по формулам численного дифференцирования?

а) Погрешность усечения вызвана заменой данной функции f(x) интерполяционным многочленом P_n(x).

б) Погрешность усечения вызвана неточным заданием исходных значений данной функции f(x).

в) Погрешность усечения вызвана неточным заданием начальным и граничных данных для исходной функции f(x).

Контрольная работа на тему: «Методы решения обыкновенных дифференциальных уравнений»

Задание №1.  Найти приближенные решения задачи Коши на отрезке [0,1] с точностью , используя явный (неявный) метод Адамса.

Вариант №1	Вариант №2	Вариант №3

Задание №2. Решить дифференциальное уравнение с заданным начальным условием методом Рунге-Кутта с шагом 0,2.

Вариант №1	Вариант №2	Вариант №3
на отрезке [1,2]	на отрезке [0,1]	на отрезке [1,2]

Тестовые задания по теме: «Методы решения обыкновенных дифференциальных уравнений»

1. К одношаговым методам решения обыкновенных дифференциальных уравнений относятся:

а) метод Эйлера

б) метод Рунге-Кутта

в) метод Адамса

2. Геометрический смысл метода Рунге-Кутта заключается в следующем:

а) определяется направление интегральной кривой в исходной точке  и во вспомогательной точке , а в качестве окончательного берется среднее значение этих направлений.

б) искомая интегральная кривая заменяется ломанной , соединяющей точки , . Причем первое звено ломанной касается истинной интегральной кривой в точке . При последовательность ломанных на отрезке стремится к искомой интегральной кривой.

в) Из точки  сдвигаются в направлении, определяемом углом , для которого . На этом направлении выбирается точка с координатами .  Затем из точки  сдвигаются в направлении, определяемым углом , для которого , и на этом направлении выбирается точка с координатами . Наконец из точки , сдвигаются в направлении, определяемом углом , для которого  и на этом направлении выбирается точка с координатами . Этим задается еще одно направление, определяемое углом , для которого . Четыре, полученные направления усредняются. На этом окончательном направлении и выбирается очередная точка .

3. С каким порядком точности по h сходится численный метод

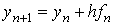
а) 3

б) 0

в) 1

4. Является ли метод , аппроксимирующий ОДУ :

а) неявным одношаговым

б) неявным двухшаговым

в) явным двухшаговым

5. Локальная оценка погрешности метода Эйлера имеет вид:

а)

б)

в)

6. Явный метод Адамса второго порядка точности 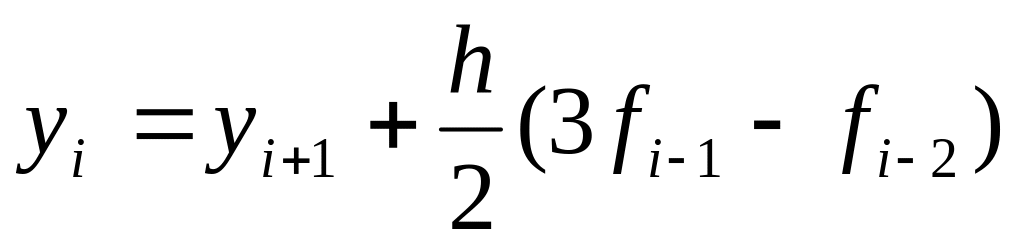можно получить, интегрируя интерполяционный многочлен

а) 1 порядка, построенный по точкам

б) 2 порядка, построенный по точкам

в) 1 порядка, построенный по точкам

7. Выберите верные утверждения.

а) Метод Рунге-Кутта обладает большей точностью, чем методы Эйлера.

б) Метод Рунге-Кутта весьма трудоемок и в сравнении с методами Эйлера, Эйлера-Коши дает большую погрешность вычислений.

в) Важным преимуществом Метода Эйлера-Коши является возможность на любом этапе вычислений изменить шаг интегрирования, при условии выполнения заданной точности.

8. Локальная оценка метода Рунге-Кутты 4-го порядка точности имеет вид:

а)

б)

в)