
Пп 9. Предел Функции основные определения и формулы
О.1.
Определение предела по Гейне (на
языке последовательностей). Число
![]() называется пределом
функции
называется пределом
функции
![]() в точке
в точке
![]() ,
если для любой
последовательности
,
если для любой
последовательности
![]() такой, что
такой, что
![]() ,
выполняется равенство
,
выполняется равенство
![]() ,
которое обозначают:
,
которое обозначают:
![]() .
.
О.2.
Определение предела по Коши (на
языке
![]() -
-
![]() ).
Число
называется пределом
функции
в точке
,
если
).
Число
называется пределом
функции
в точке
,
если
![]() .
.

Понятие |
Обозначение |
Определение |
Предел
функции
|
|
|
- бесконечно большая функция в точке |
|
|
|
|
|
|
|
|
Предел
функции
при
|
|
|
|
|
|
-
бесконечно большая функция при
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Односторон-ние пределы справа и слева |
|
|
|
|
|
-
бесконечно большая функция справа и
слева от точки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бесконечно малые и бесконечно большие функции и их свойства
Функция
![]() называется бесконечно
малой
в точке
называется бесконечно
малой
в точке
![]() ,
если
,
если
![]() .
.
Функция
![]() называется бесконечно
большой в
точке
,
если
.
Записывается это как
называется бесконечно
большой в
точке
,
если
.
Записывается это как
![]() .
.
Свойства:
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
![]() .
Произведение
бесконечно малой функции на ограниченную
функцию есть функция бесконечно малая.
.
Произведение
бесконечно малой функции на ограниченную
функцию есть функция бесконечно малая.
![]() .
Произведение
бесконечно малых функций есть функция
бесконечно малая.
.
Произведение
бесконечно малых функций есть функция
бесконечно малая.
![]() .
Если
.
Если
![]() ,
то
,
то

![]() .Если
.Если
![]() - бесконечно малая функция при
- бесконечно малая функция при
![]() и
и
![]() при
при
![]() ,
то
,
то
![]() - бесконечно большая функция при
.
Если
- бесконечно большая функция при
.
Если
![]() - бесконечно
большая, то
- бесконечно малая.
- бесконечно
большая, то
- бесконечно малая.
6˚. Произведение бесконечно большой функции на ограниченную функцию, не равную нулю, есть функция бесконечно большая.
7˚. Произведение бесконечно больших функций есть функция бесконечно большая.
Свойства функций, имеющих предел
|
где
|
где
|
Если
![]() и
и
![]() ,
то
,
то
![]()
![]()
![]()
 где
где
![]() .
.
Если
функции
![]() и
и
![]() имеют одну область определения
имеют одну область определения
![]() и
и
![]() ,
то
,
то
![]()
Теорема о пределе промежуточной функции.
Если
1)
![]() ,
2)
,
2)
![]() ,
,
то
![]() .
.
Замечательные пределы
Первый
замечательный предел
![]() :
:
![]() .
.
Второй
замечательный предел
![]() :
:
 ;
;
![]() .
.

Сравнение бесконечно малых функций
Для бесконечно малых выполняется:
1)
1(x)
и 2(x)
одного
порядка,
если
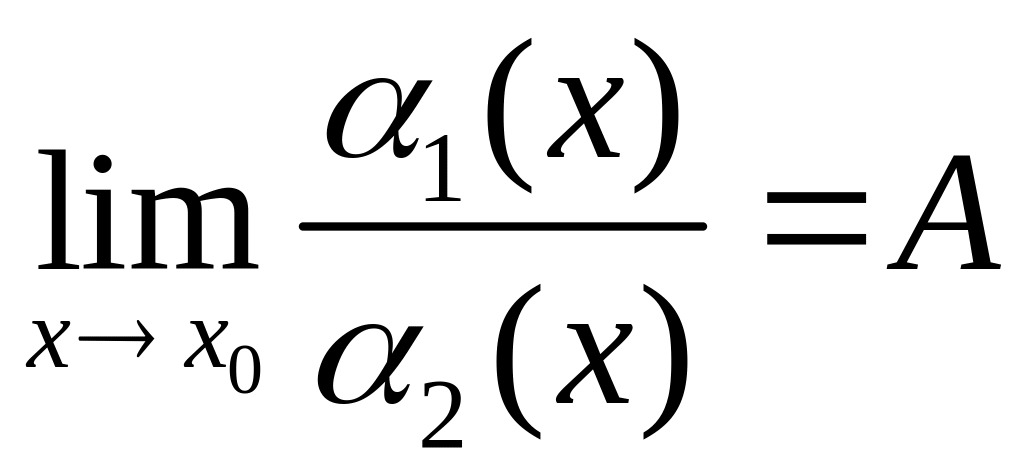 ,
A
< ;
,
A
< ;
2)
1(x)
2(x)
- эквивалентные,
если
 ;
;
3)
1(x)
= о
(2(x))
- 1(x)
бесконечно малая более
высокого порядка малости по
сравнению с 2(x),
если
 ;
;
4)
если 1(x)
2(x),
3(x)
4(x),
то

Эквивалентные бесконечно малые при x 0:
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.

