
Пп 6. Аналитическая геометрия в пространстве: плоскость и прямая линия в пространстве, взаимное расположение прямой и плоскости. Формулы аналитической геометрии в пространстве
6.1. Плоскость в пространстве
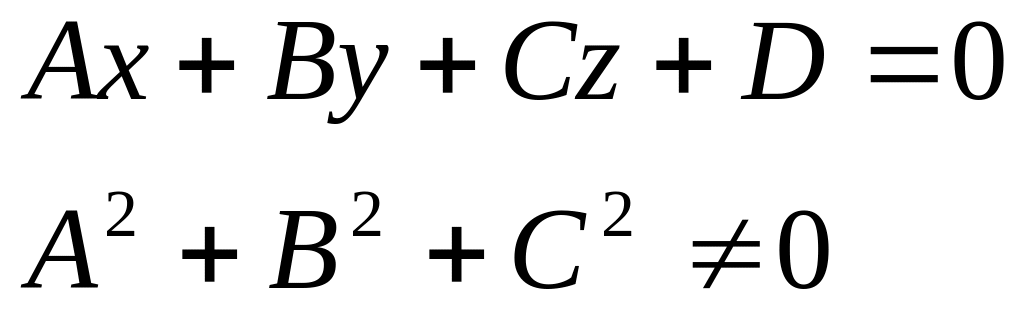 -
общее уравнение плоскости в декартовой
системе координат ;
-
общее уравнение плоскости в декартовой
системе координат ;
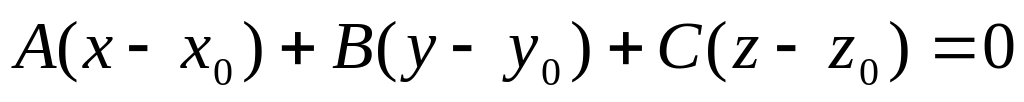 -
уравнение плоскости, проходящей через
заданную точку
-
уравнение плоскости, проходящей через
заданную точку
 и перпендикулярной вектору
и перпендикулярной вектору
 ;
;
 -
уравнение плоскости, отсекающей на
осях координат ox,
oy,
oz
отрезки a,
b
и
c
соответственно;
-
уравнение плоскости, отсекающей на
осях координат ox,
oy,
oz
отрезки a,
b
и
c
соответственно;
 -
нормальное уравнение плоскости, где р
– расстояние
от начала координат до плоскости, а
единичный вектор, перпендикулярный
плоскости, имеет координаты
-
нормальное уравнение плоскости, где р
– расстояние
от начала координат до плоскости, а
единичный вектор, перпендикулярный
плоскости, имеет координаты
 ;
;
 -
нормальный вид общего уравнения
плоскости (знак нормирующего множителя
противоположен знаку D);
-
нормальный вид общего уравнения
плоскости (знак нормирующего множителя
противоположен знаку D);
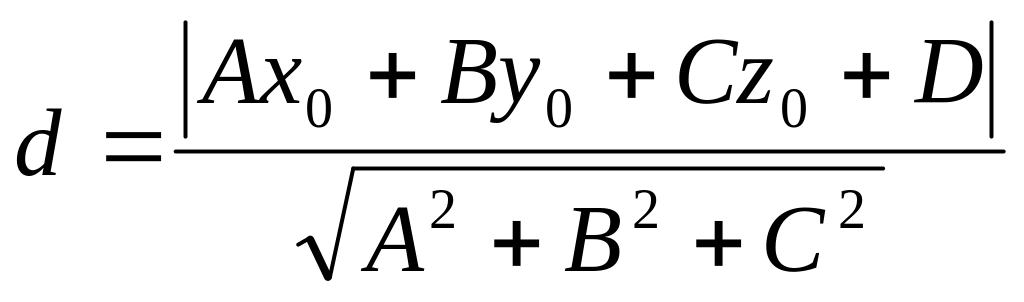 -
расстояние от точки
до плоскости, заданной общим уравнением;
-
расстояние от точки
до плоскости, заданной общим уравнением;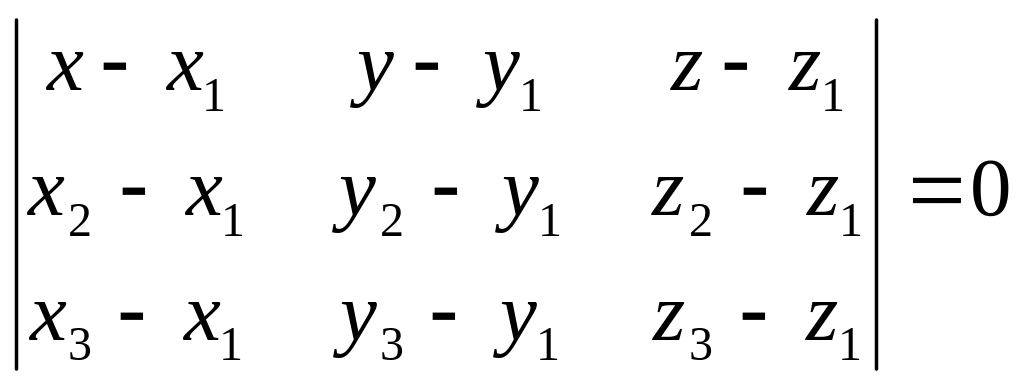 -
уравнение плоскости, проходящей через
три точки
-
уравнение плоскости, проходящей через
три точки
 (i=1,2,3),
не лежащие на одной прямой;
(i=1,2,3),
не лежащие на одной прямой;
 -
угол
-
угол
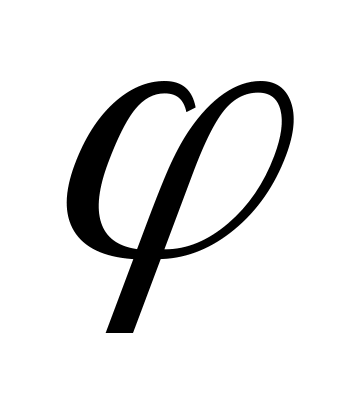 между плоскостями
между плоскостями
 ;
;
 -
необходимое и достаточное условие
параллельности плоскостей
-
необходимое и достаточное условие
параллельности плоскостей

 -
необходимое и достаточное условие
перпендикулярности плоскостей
-
необходимое и достаточное условие
перпендикулярности плоскостей
 ;
;
 -
расстояние между двумя параллельными
плоскостями
-
расстояние между двумя параллельными
плоскостями
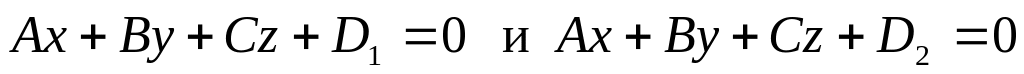 .
.
6.2. Прямая в пространстве
 -
общее уравнение прямой как линии
пересечения двух параллельных плоскостей;
-
общее уравнение прямой как линии
пересечения двух параллельных плоскостей; -
канонические уравнения прямой, проходящей
через точку
и имеющей направляющий вектор с
компонентами
-
канонические уравнения прямой, проходящей
через точку
и имеющей направляющий вектор с
компонентами
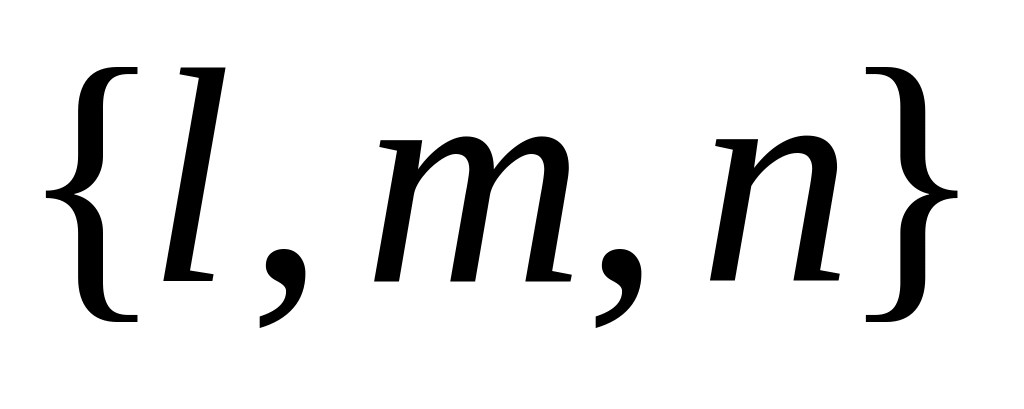 ;
; -
уравнения прямой в виде проекций на
координатные плоскости;
-
уравнения прямой в виде проекций на
координатные плоскости;
 -
параметрические уравнения прямой,
проходящей через точку
и имеющей направляющий вектор с
компонентами
;
-
параметрические уравнения прямой,
проходящей через точку
и имеющей направляющий вектор с
компонентами
;
 -
соотношения между компонентами
направляющего вектора прямой и
координатами общего уравнения прямой;
-
соотношения между компонентами
направляющего вектора прямой и
координатами общего уравнения прямой;
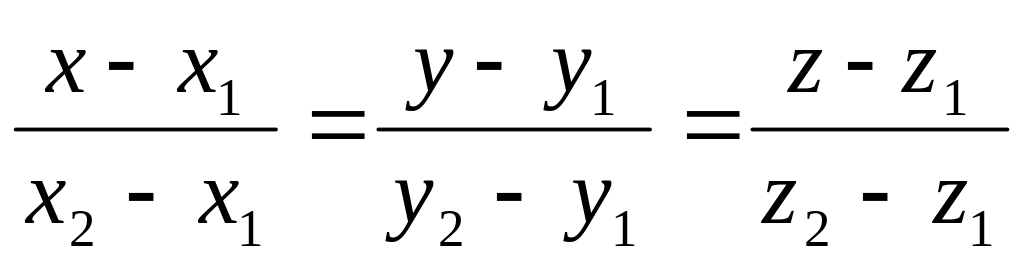 -
канонические уравнения прямой, проходящей
через точки с координатами
(i=1,2);
-
канонические уравнения прямой, проходящей
через точки с координатами
(i=1,2);
 -
косинус угла
между прямыми
-
косинус угла
между прямыми
 (i=1,2),
проходящими через точку
;
(i=1,2),
проходящими через точку
;
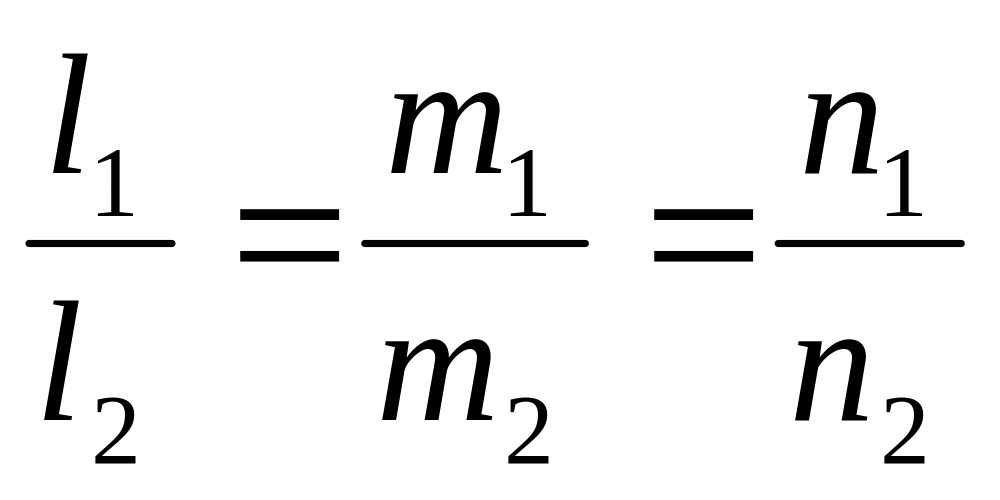 -
условие параллельности двух прямых
(i=1,2);
-
условие параллельности двух прямых
(i=1,2);
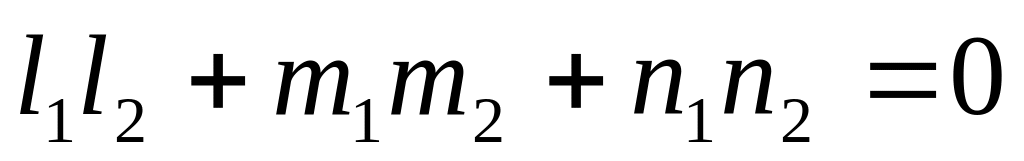 -
условие перпендикулярности двух прямых
(i=1,2);
-
условие перпендикулярности двух прямых
(i=1,2);
 -
прямые:
-
прямые:
![]()
 и
и
![]()
 лежат
в одной плоскости
лежат
в одной плоскости
6.3. Прямая и плоскость в пространстве
 уравнение
пучка плоскостей, проходящих через
прямую, заданную общим уравнением
уравнение
пучка плоскостей, проходящих через
прямую, заданную общим уравнением

 -
координаты точки пересечения прямой
и плоскости
-
координаты точки пересечения прямой
и плоскости
 ;
;
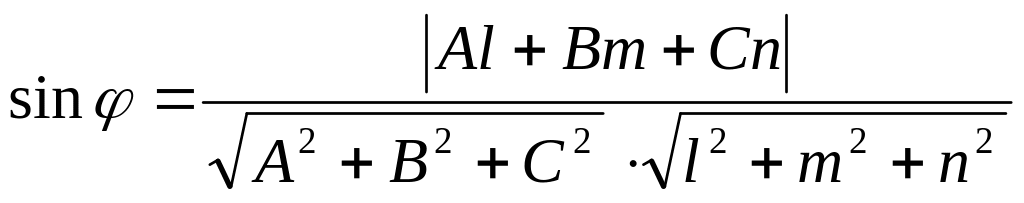 -
синус угла между прямой
и плоскостью
;
-
синус угла между прямой
и плоскостью
; -
условие перпендикулярности прямой
и плоскости
;
-
условие перпендикулярности прямой
и плоскости
;
 -
условие параллельности прямой
и плоскости
.
-
условие параллельности прямой
и плоскости
.
РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
В ПРОСТРАНСТВЕ
Плоскость
ПП
6.№1.
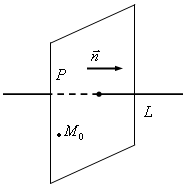
Составьте уравнение плоскости Р,
проходящей через точку
![]() :
:
6.1.1)
параллельно плоскости
![]() ;
;
6.1.2) перпендикулярно прямой L;
6.1.3)
перпендикулярно двум плоскостям
![]() .
.
Решение:
6 .1.1)
Плоскость
проходит через точку
.1.1)
Плоскость
проходит через точку
![]() параллельно
плоскости
,
заданной уравнением
параллельно
плоскости
,
заданной уравнением
![]() .
В качестве нормального вектора искомой
плоскости Р
можно выбрать нормальный вектор
плоскости
.
Плоскость
задана общим уравнением
.
В качестве нормального вектора искомой
плоскости Р
можно выбрать нормальный вектор
плоскости
.
Плоскость
задана общим уравнением
![]() ,
в котором коэффициенты А,
В, С
являются компонентами нормального
,
в котором коэффициенты А,
В, С
являются компонентами нормального
вектора,
значит,
![]() и уравнение плоскости Р
может быть записано в виде уравнения
плоскости, проходящей через точку
и уравнение плоскости Р
может быть записано в виде уравнения
плоскости, проходящей через точку
![]() с нормальным вектором
:
с нормальным вектором
:
![]() .
После приведения к виду общего уравнения
плоскости это уравнение принимает вид:
.
После приведения к виду общего уравнения
плоскости это уравнение принимает вид:
![]() .
.
ОТВЕТ:
![]() .
.
6.1.2)
Плоскость
проходит через точку
![]() перпендикулярно
перпендикулярно
прямой
L:![]() .
В качестве нормального вектора искомой
плоскости выбираем направляющий вектор
прямой L,
имеющий компоненты
.
В качестве нормального вектора искомой
плоскости выбираем направляющий вектор
прямой L,
имеющий компоненты
![]() из канонических уравнений данной прямой
L.
из канонических уравнений данной прямой
L.
Уравнение
плоскости, проходящей через точку
с
нормальным вектором
![]() ,
имеет вид:
,
имеет вид:
![]() .
.
ОТВЕТ:
![]() .
.
6.1.3)
Искомая
плоскость проходит через точку
![]() и
и
п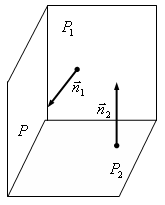 ерпендикулярна
двум плоскостям:
ерпендикулярна
двум плоскостям:
![]()
Нормальный вектор искомой плоскости
должен быть перпендикулярен нормальным
векторам
плоскостей
![]() и
и![]() .
В качестве
.
В качестве
такого вектора можно выбрать их векторное
произведение:

Уравнение искомой плоскости имеет вид:
![]() .
.
ОТВЕТ:
![]() .
.
ПП 6.№2. Составьте уравнение плоскости Р , проходящей через три
данные
точки:![]()
Решение:
Если M(x,y,z)
- текущая координата плоскости, то
уравнение плоскости получается как
следствие компланарности векторов
![]() ,
то есть равенства нулю их смешанного
произведения:
,
то есть равенства нулю их смешанного
произведения:

ОТВЕТ:
![]()
ПП 6.№3.
6.3.1)
Найдите отрезки, отсекаемые плоскостью
![]() на координатных осях.
на координатных осях.
6.3.2)
Составьте уравнение плоскости Р,
параллельной вектору
![]() и отсекающей на координатных осях
отрезки
и отсекающей на координатных осях
отрезки
![]() .
.
6.3.3)
Напишите уравнение плоскости, проходящей
через точку
![]() и отсекающей от осей координат
положительные и равные отрезки.
и отсекающей от осей координат
положительные и равные отрезки.
Решение:
6.3.1) Приведем уравнение плоскости к виду уравнения
плоскости "в отрезках":
![]()
![]() отсекаемые
плоскостью на осях ox,
oy, oz
соответственно.
отсекаемые
плоскостью на осях ox,
oy, oz
соответственно.
ОТВЕТ: -4, 3, 0,5.
6.3.2)
Уравнение искомой плоскости "в
отрезках" имеет вид:
![]() Приведение его к общему виду
Приведение его к общему виду
![]() дает плоскость с нормальным вектором
дает плоскость с нормальным вектором
![]() Из условия перпендикулярности векторов
Из условия перпендикулярности векторов
![]() :
:
![]()
![]() ,
и уравнение плоскости принимает вид:
,
и уравнение плоскости принимает вид:
![]() .
.
ОТВЕТ:
![]() .
.
6.3.3)
Уравнение плоскости, отсекающей от осей
координат положительные и равные отрезки
а, имеет вид:
![]()
Так
как плоскость проходит через точку![]() ,
,
![]() и уравнение плоскости принимает вид:
и уравнение плоскости принимает вид:![]() .
.
ОТВЕТ:
![]() .
.
ПП
6.№4.
Найдите
угол между плоскостями
![]() и
и
![]() .
.
Решение:
Один
из двух смежных углов (острый) между
плоскостями равен углу между их
нормальными векторами
![]() и находится из их скалярного произведения:
и находится из их скалярного произведения:
![]()
ОТВЕТ:
![]()
ПП
6.№5.
Найдите
уравнение плоскости, проходящей через
точки
![]() и
и
![]() перпендикулярно
к плоскости
перпендикулярно
к плоскости
![]()
Решение:
Уравнение плоскости, проходящей через
точку М
с нормальным вектором
,
условие прохождения этой плоскости
через точку N
и условие перпендикулярности этой
плоскости и заданной плоскости с
нормальным вектором
![]() дают однородную систему уравнений для
определения А,
В, С:
дают однородную систему уравнений для
определения А,
В, С:

Условие
существования решения системы
 приводит к уравнению искомой плоскости:
приводит к уравнению искомой плоскости:
![]()
ОТВЕТ:
ПП
6.№6.
Приведите
уравнение плоскости
![]() к нормальному виду и объясните смысл
коэффициентов при неизвестных.
к нормальному виду и объясните смысл
коэффициентов при неизвестных.
Решение: В нормальном уравнении плоскости
коэффициенты
представляют собой направляющие косинусы
единичного вектора нормали к этой
плоскости, которая проходит через начало
координат и отстоит от него на расстоянии
р.
Общее уравнение плоскости
с нормальным вектором
приводится к нормальному виду путем
умножения на нормирующий множитель
![]() знак которого противоположен знаку D.
знак которого противоположен знаку D.
В
данной задаче
![]() и уравнение плоскости принимает вид:
и уравнение плоскости принимает вид:
![]()
![]()
ОТВЕТ:
ПП
6.№7.
Найдите расстояние от заданной точки
![]() до плоскости
.
до плоскости
.
Решение:
Расстояние от точки
до плоскости с нормальным вектором
![]() равняется
равняется
![]() .
.
Здесь
![]() ,
то есть начало координат и точка
находятся по одну сторону от плоскости.
Искомое расстояние равно
,
то есть начало координат и точка
находятся по одну сторону от плоскости.
Искомое расстояние равно
![]()
ОТВЕТ: 3.
ПП
6.№8.
Составьте уравнение плоскости, которая
делит пополам двугранный угол,
образованный двумя пересекающимися
плоскостями:![]() и
и
![]()
Решение:
Уравнение
плоскостей найдем из условия равенства
отклонений точки этой плоскости
![]() от двух данных плоскостей
и
от двух данных плоскостей
и
![]() :
:
![]() что
дает
что
дает
1)
![]() :
:
![]()
2)
![]() :
:

О ТВЕТ:
ТВЕТ:
![]() ,
,![]()
Прямая
ПП
6.№9.
Прямая L
задана общими уравнениями
 Напишите
канонические уравнения этой прямой и
её уравнения в виде проекций на
координатные плоскости.
Напишите
канонические уравнения этой прямой и
её уравнения в виде проекций на
координатные плоскости.
Решение:
Решим задачу двумя способами.
1-й способ.
Найдем произвольную точку, лежащую на прямой, предположив, что
x = 0, тогда из системы, задающей прямую двумя уравнениями плоскости, найдем, что y = 2 и z = 2.
Точка
![]() .
В качестве направляющего вектора прямой
можно выбрать вектор
.
В качестве направляющего вектора прямой
можно выбрать вектор
![]() ,
так как он будет перпендикулярен как
,
так как он будет перпендикулярен как
![]() ,
так и
,
так и
![]() :
:
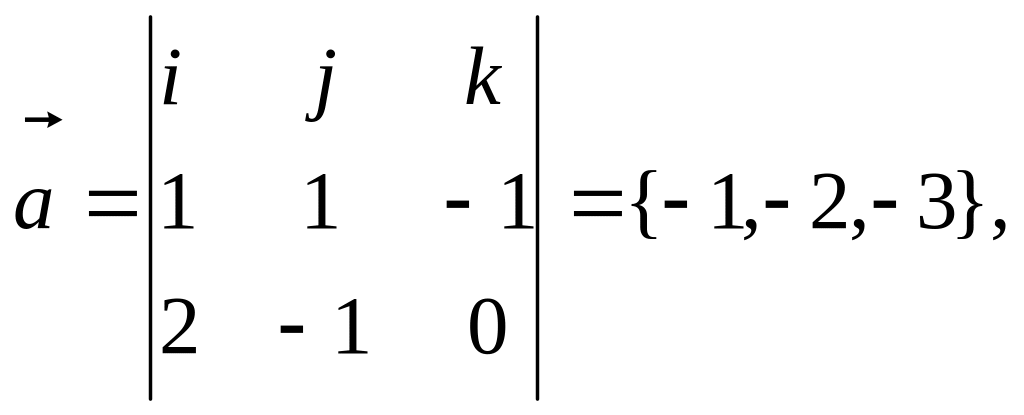 и канонические уравнения прямой принимают
вид:
и канонические уравнения прямой принимают
вид:
![]() и могут быть записаны в виде проекций
на координатные плоскости следующим
образом:
и могут быть записаны в виде проекций
на координатные плоскости следующим
образом:
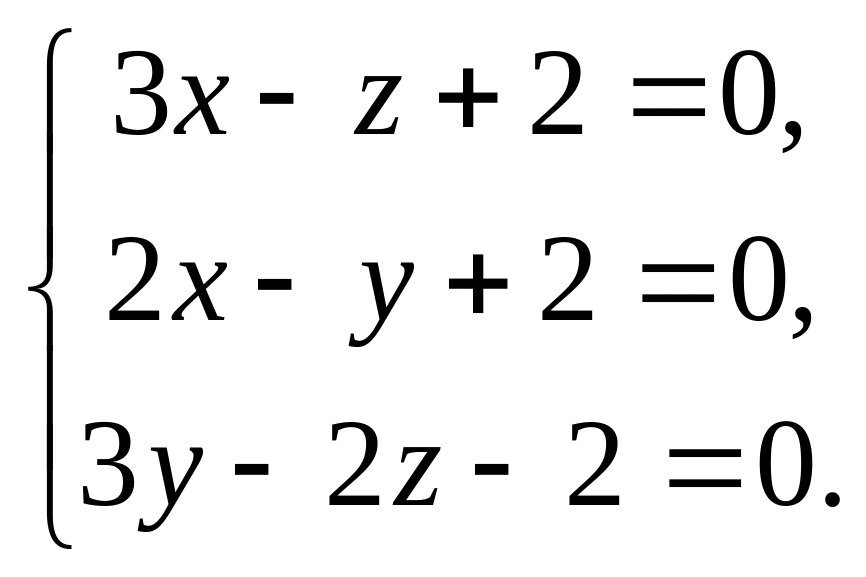
2-й способ.
Из общих уравнений прямой L , исключая x и y в системе, получим уравнения прямой в проекциях на плоскости xoz и yoz:

Из
этих уравнений
![]() и канонические уравнения прямой можно
записать в виде
и канонические уравнения прямой можно
записать в виде![]()
ОТВЕТ:
;
![]() ;
;
ПП 6.№10.
6.10.1) Докажите параллельность прямых
![]()
6.10.2) Определите угол между прямыми
![]()
Решение:
6.10.1)
Направляющий вектор прямой
![]() имеет
вид:
имеет
вид:
![]() .
Направляющий вектор прямой
.
Направляющий вектор прямой
![]() может быть выбран в виде векторного
произведения нормальных векторов двух
пересекающихся плоскостей
может быть выбран в виде векторного
произведения нормальных векторов двух
пересекающихся плоскостей
![]()
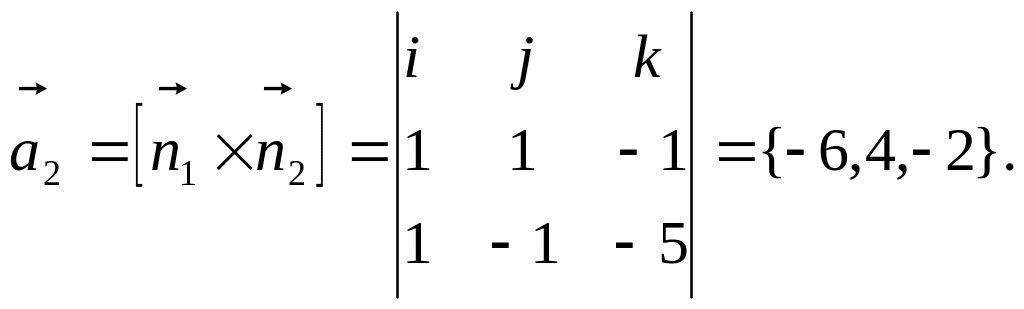
Прямые
и
параллельны, так как компоненты их
направляющих векторов пропорциональны:
![]() .
.
6.10.2)
Угол между направляющими векторами
прямых
и
![]() определяется из значения их скалярного
произведения:
определяется из значения их скалярного
произведения:
![]()
![]()
ОТВЕТ:
![]()
ПП
6.№11.
Найдите уравнения прямой, проходящей
через точку
![]() и пересекающей ось ox
под прямым углом.
и пересекающей ось ox
под прямым углом.
Решение:
Уравнение искомой прямой можно записать
в виде уравнения прямой, проходящей
через две точки
![]() и
и
![]() :
:
.
По условию
![]()
Вторую
точку находим из условия, что прямая
перпендикулярна оси ox
и пересекает
ее, то есть
![]() и
уравнение искомой прямой принимает
вид:
и
уравнение искомой прямой принимает
вид:
![]()
ОТВЕТ:
ПП 6.№12.
6.12.1)
Составьте параметрические уравнения
прямой L,
проходящей через точку
![]() параллельно прямой
параллельно прямой
![]()
6.12.2)
Напишите канонические уравнения прямой
L,
проходящей через точку
параллельно прямой
![]()
Решение:
6.12.1)
В качестве направляющего вектора
искомой прямой L
можно взять направляющий вектор прямой
:
![]() ,
так как прямые L
и
параллельны по условию; канонические
уравнения прямой
,
так как прямые L
и
параллельны по условию; канонические
уравнения прямой
![]() могут быть приведены к параметрическому
виду, если приравнять входящие в них
отношения значению параметра t:
могут быть приведены к параметрическому
виду, если приравнять входящие в них
отношения значению параметра t:
![]()
ОТВЕТ:
6.12.2)
Прямая L,
параллельная прямой
,
будет перпендикулярна нормальным
векторам
![]() плоскостей, образующих прямую
,
то есть
плоскостей, образующих прямую
,
то есть
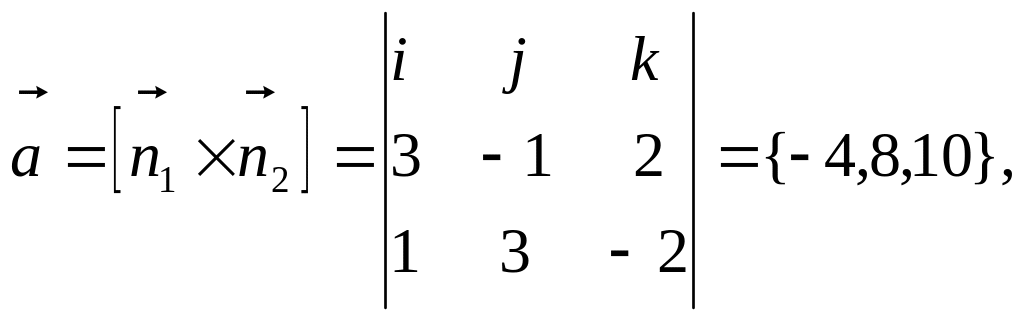 и
канонические уравнения прямой
L принимают
вид:
и
канонические уравнения прямой
L принимают
вид:
![]()
ОТВЕТ:
ПП
6.№13.
Определите,
при каком значении
![]() прямые
прямые
![]() пересекаются.
пересекаются.
Решение:
По
условию прямая
проходит через точку
![]() ,
а прямая
- через точку
,
а прямая
- через точку
![]() .
.
Условием
пересечения двух прямых будет условие
компланарности векторов
![]() ,
которое можно записать в виде
,
которое можно записать в виде
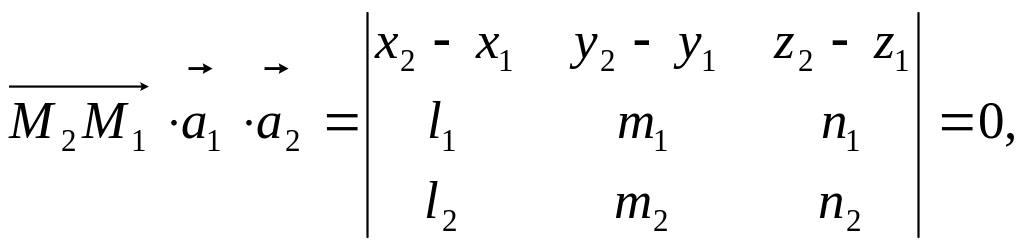
то
есть
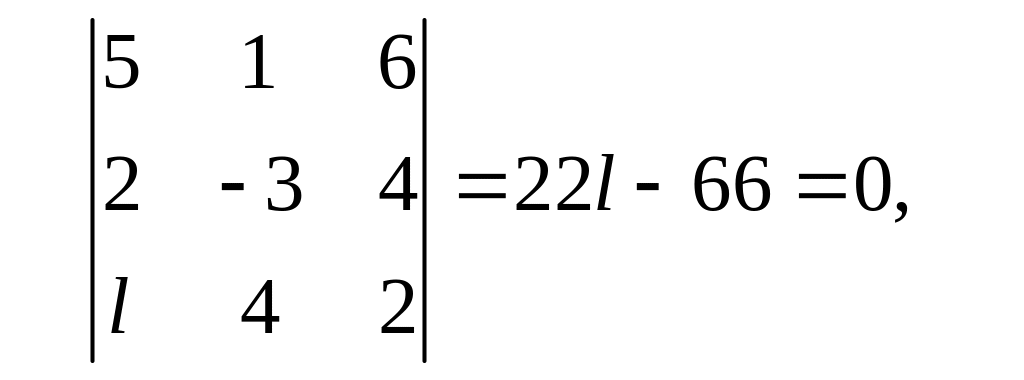 откуда
откуда
![]()
ОТВЕТ: 3.
ПП
6.№14.
Составьте уравнение прямой, проходящей
через точку
![]() ,
пересекающей прямую
,
пересекающей прямую
![]() и перпендикулярную прямой
и перпендикулярную прямой
![]()
Решение:
Уравнение
искомой прямой
![]() .
Она лежит в одной плоскости с прямой
,
проходящей через точку
.
Она лежит в одной плоскости с прямой
,
проходящей через точку
![]() ,
то есть
,
то есть
 и перпендикулярна прямой
с направляющим вектором
и перпендикулярна прямой
с направляющим вектором
![]() .
Условие перпендикулярности прямых
заключается в равенстве
.
Условие перпендикулярности прямых
заключается в равенстве
![]() Решим систему
Решим систему
![]() для определения
для определения
![]() Выражая
Выражая
![]() через
через
![]() найдем
найдем
![]()
![]() при
при
![]() таким образом,
таким образом,
![]() и уравнение искомой прямой L
имеет вид:
и уравнение искомой прямой L
имеет вид:
![]()
ОТВЕТ:
