
Пп № 4. Векторная алгебра Основные определения и формулы
В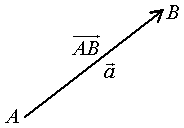 ектор
- направленный отрезок.
ектор
- направленный отрезок.
Векторы коллинеарными, если лежат на одной прямой, либо на параллельных прямых.
Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
![]() - два вектора равны,
если они коллинеарны, имеют одинаковую
длину и направление.
- два вектора равны,
если они коллинеарны, имеют одинаковую
длину и направление.
Линейные операции над векторами
С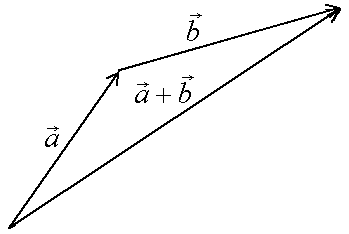 уммой
уммой
![]() двух векторов
двух векторов
![]() и
и
![]() называется вектор, идущий из начала
вектора
в конец вектора
при условии, что начало вектора
приложено к концу вектора
(правило треугольника).
называется вектор, идущий из начала
вектора
в конец вектора
при условии, что начало вектора
приложено к концу вектора
(правило треугольника).
Свойства:
1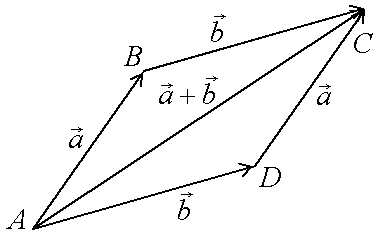 ˚.
˚. ![]()
2˚. ![]()
3˚. ![]()
4 ˚. Для
каждого вектора
существует противоположный ему вектор
˚. Для
каждого вектора
существует противоположный ему вектор
![]() ,
такой, что
,
такой, что
![]() .
.
Разностью векторов
и
будет вектор
![]() ,
,
идущий из конца вектора к концу вектора .
Произведением
![]() вектора
на вещественное число
вектора
на вещественное число
![]() .
.
Свойства операции умножения вектора на число:
5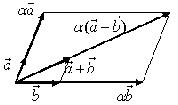 ˚.
˚. ![]()
6˚. ![]()
7˚. ![]()
8˚. ![]()
Линейная зависимость векторов. Геометрические критерии линейной зависимости
Линейной комбинацией
векторов
![]() называют выражение:
называют выражение:
![]() ,
,
где
![]() - произвольные действительные числа.
- произвольные действительные числа.
Система векторов называется линейно зависимой, если существуют действительные числа , такие, что хотя бы одно из них отлично от нуля, и выполняется равенство:
![]() .
(*)
.
(*)
В противном случае,
т.е. если линейная комбинация (*) обращается
в ноль только при всех
![]() ,
то система векторов называется линейно
независимой.
,
то система векторов называется линейно
независимой.
Если векторы линейно зависимы, то любой вектор может быть выражен в виде линейной комбинации остальных.
Геометрические критерии линейной зависимости
Система двух ненулевых
векторов
![]() линейно зависима тогда, и только тогда,
когда векторы коллинеарны.
линейно зависима тогда, и только тогда,
когда векторы коллинеарны.
Система трех векторов
![]() линейно зависима тогда и только тогда,
когда векторы компланарны.
линейно зависима тогда и только тогда,
когда векторы компланарны.
Базис и координаты
Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке.
Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Базисом на прямой будем называть любой ненулевой вектор этой прямой.
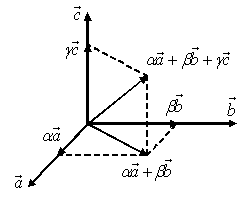 Каждый
вектор может быть разложен по базису в
пространстве и это разложение единственно.
Каждый
вектор может быть разложен по базису в
пространстве и это разложение единственно.
Коэффициенты разложения вектора по базису называются координатами вектора в данном базисе и в каждом базисе определяются однозначно:
![]() .
.
При сложении двух векторов
![]() и
и
![]() их координаты (относительно любого
базиса) складываются. При умножении
вектора
на любое число
все его координаты умножаются на это
число.
их координаты (относительно любого
базиса) складываются. При умножении
вектора
на любое число
все его координаты умножаются на это
число.
Системой координат
в пространстве называют совокупность
базиса
![]() и некоторой точки, называемой началом
координат.
и некоторой точки, называемой началом
координат.
Вектор
![]() ,
идущий из начала координат в точку
,
идущий из начала координат в точку
![]() ,
называется радиус-вектором точки
.
,
называется радиус-вектором точки
.
Координатами точки
![]() называются координаты вектора
.
называются координаты вектора
.
Таким образом, координаты радиус-вектора и координаты точки совпадают.
Ортонормированный базис. Декартова прямоугольная система координат
Пусть в качестве базиса выбраны три взаимно перпендикулярных вектора с длинами, равными единице.
Обозначения:
![]() ,
,
![]()
Т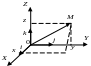 акой
базис называется ортонормированным
(ОНБ). Векторы
акой
базис называется ортонормированным
(ОНБ). Векторы
![]() называются базисными ортами. Зафиксируем
точку О
– начало координат и отложим от нее
векторы
.
Полученная система координат называется
прямоугольной
декартовой.
Координаты любого вектора в этом базисе
называются декартовыми координатами
вектора:
называются базисными ортами. Зафиксируем
точку О
– начало координат и отложим от нее
векторы
.
Полученная система координат называется
прямоугольной
декартовой.
Координаты любого вектора в этом базисе
называются декартовыми координатами
вектора:
![]()
Прямые линии,
проведенные через начало координат по
направлениям базисных векторов,
называются координатными осями:
![]() –
порождает
–
порождает
![]() ;
;
![]() – порождает
– порождает
![]() ;
;![]() –
порождает
–
порождает
![]() .
Координаты точки М
(вектора
)
в декартовой системе координат по осям
,
,
называются соответственно абсциссой,
ординатой и аппликатой.
.
Координаты точки М
(вектора
)
в декартовой системе координат по осям
,
,
называются соответственно абсциссой,
ординатой и аппликатой.
Декартовы прямоугольные координаты
![]() вектора
равны проекциям этого вектора на оси
,
,
соответственно; другими словами,
вектора
равны проекциям этого вектора на оси
,
,
соответственно; другими словами,
![]() ,
,
![]() ,
,
![]() .
.
Здесь
![]() – углы, которые составляет вектор
с координатными осями
,
,
соответственно, при этом
– углы, которые составляет вектор
с координатными осями
,
,
соответственно, при этом
![]() ,
,
![]() ,
,
![]() называются направляющими косинусами
вектора
.
называются направляющими косинусами
вектора
.
Вектор
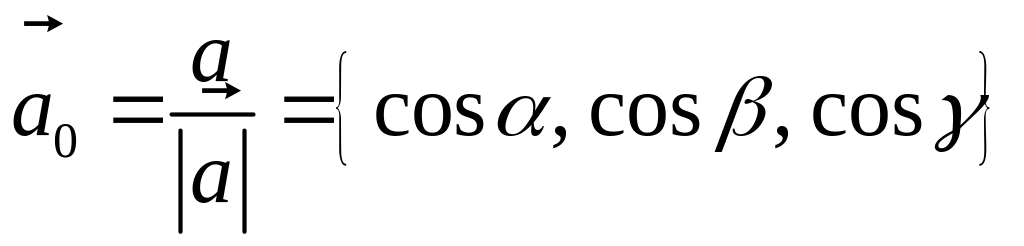 представляет собой вектор единичной
длины данного направления, или орт
данного направления. Для направляющих
косинусов справедливо соотношение:
представляет собой вектор единичной
длины данного направления, или орт
данного направления. Для направляющих
косинусов справедливо соотношение:
![]() .
.
П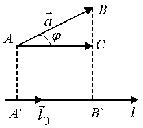 роекция
вектора
на ось l
-
величина А`В`
равна
роекция
вектора
на ось l
-
величина А`В`
равна
![]() ,
где
,
где
![]() - орт оси l.
- орт оси l.
Скалярным произведением
двух векторов называется число,
равное произведению длин этих векторов
на косинус угла между ними:
![]() .
.
Если
![]() ,
,
![]() ,
то
,
то
![]() .
.
Алгебраические и геометрические свойства:
1°. Переместительное
свойство:
![]() .
.
2°. Сочетательное
свойство:
![]()
3°. Распределительное
свойство:
![]() ,
,
![]() .
.
4°.
![]() ,
если
,
если
![]() ,
и
,
и
![]() ,
если
,
если
![]() .
.
5°.
![]() ;
;
![]() .
.
6°.
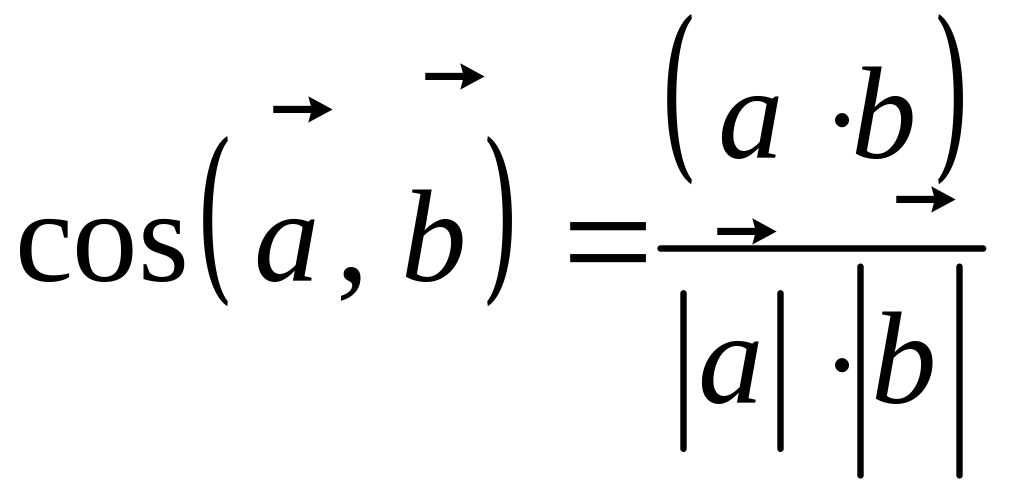
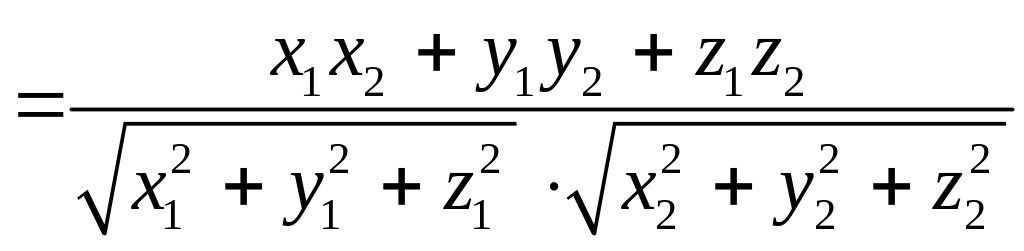 .
.
7°.
![]() =
=![]()
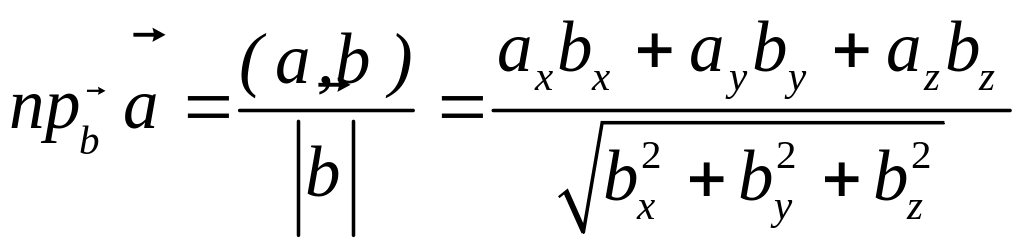 ,
,
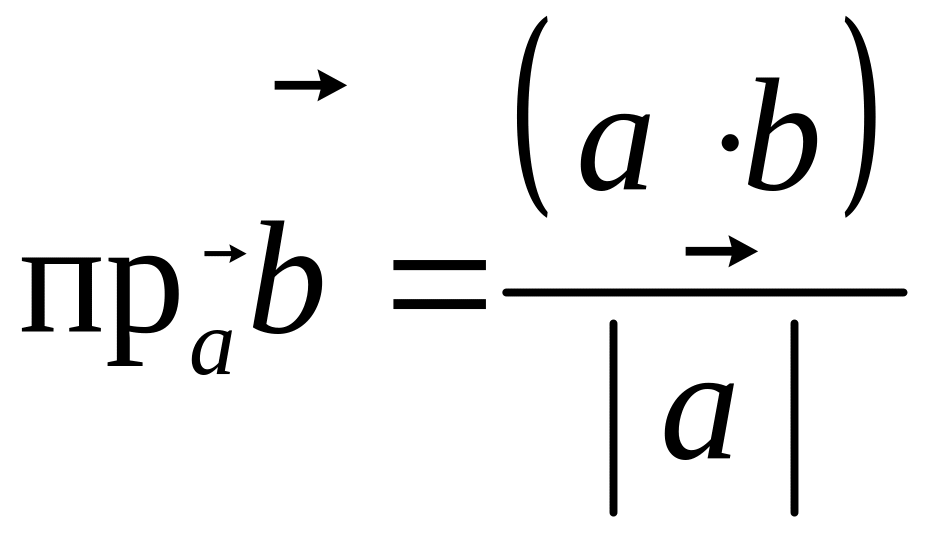 .
.
8°.
![]() :
:
![]() - условие перпендикулярности.
- условие перпендикулярности.
9°.
![]() ,
,
![]() - длина вектора.
- длина вектора.
10°.
![]() ,
,
![]() ,
,
![]() – расстояние между двумя точками.
– расстояние между двумя точками.
11°. Направляющие
косинусы вектора:
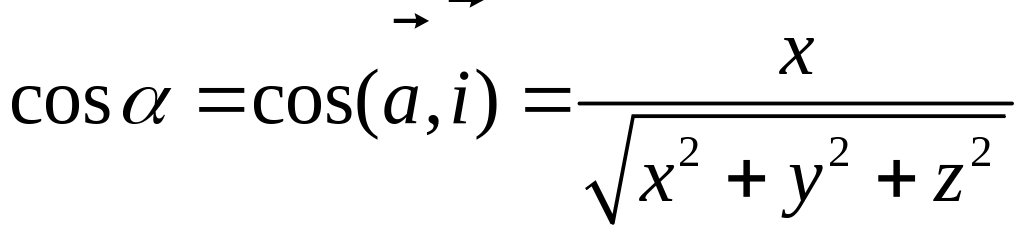 ,
,
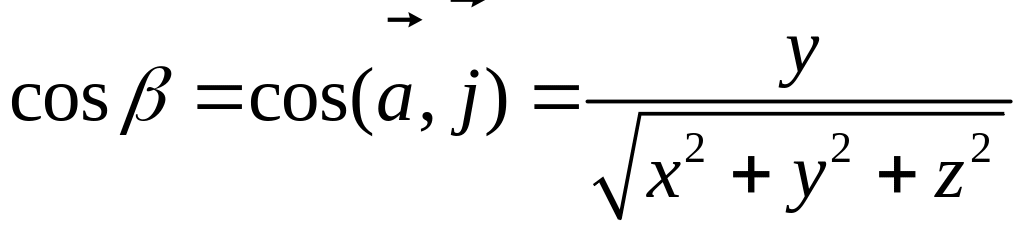 ,
,
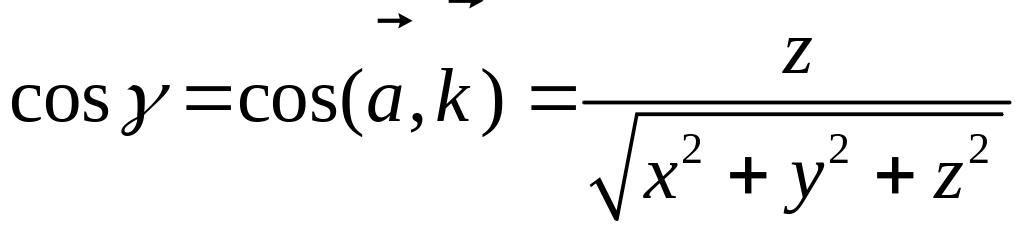 ;
cos2
α
+ cos2
β
+ cos2
;
cos2
α
+ cos2
β
+ cos2
![]() = 1
= 1
ПП 4.1. Векторы, базисы, координаты |
||
№ п/п |
Задание |
Ответ |
ПП 4 .№1 |
З РЕШЕНИЕ: Воспользуемся правилом треугольника:
Здесь
Но
Подставим
|
= |
ПП 4 .№2 |
В РЕШЕНИЕ:
Пусть
Найдем:
После последовательных подстановок
то есть
|
= |
ПП 4 .№3 |
В РЕШЕНИЕ:
Пусть
,
,
Воспользуемся свойством биссектрисы треугольника:
Отсюда следует, что
|
|
|
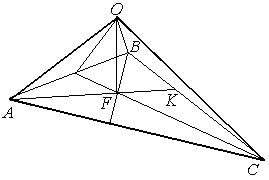
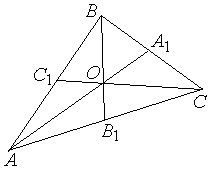
ПП 4. №4 |
В треугольнике
РЕШЕНИЕ:
О |
|
|
ПП 4 .№5 |
Д РЕШЕНИЕ:
Пусть
Отложим от вершины
по медиане
Но это координаты
вектора
|
ПП 4 .№6 |
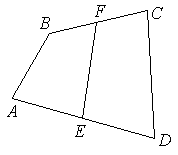
Т РЕШЕНИЕ:
Если
- трапеция, стороны
и
|
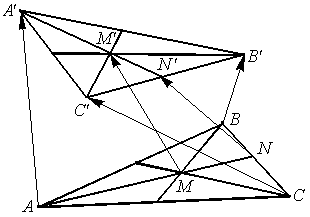
ПП 4.2. Переход к новому базису. Преобразование координат |
||
ПП 4. №7 |
В пространстве
РЕШЕНИЕ: Проверим, что - базис в пространстве :
значит
Найдем координаты вектора в базисе двумя способами.
1-й
способ:
2-й способ: Запишем матрицу преобразования координат базиса к базису :
Найдем
Координаты вектора
|
или
|
|
ПП 4.3. Построение ортогонального базиса |
|
ПП 4 .№8 |
Применяя
последовательный процесс ортогонализации
Шмидта к системе векторов
РЕШЕНИЕ: Процесс ортогонализации состоит в следующем. Из неортогонального базиса строят новый, ортогональный базис по формулам:
Проделаем эту процедуру.
Осталось нормировать
базис
|
, , . |
ПП 4.4. Декартов прямоугольный базис |
||
Направляющие косинусы и координаты |
||
ПП 4 .№9 |
В РЕШЕНИЕ:
|
3 |
ПП 4 .№10 |
Даны точки
РЕШЕНИЕ:
|
-6 |
ПП 4 .№11 |
Дан модуль вектора
РЕШЕНИЕ:
=
|
|
ПП 4. №12 |
Даны векторы
РЕШЕНИЕ:
|
, ,
|
ПП 4 .№13 |
Может ли вектор составлять с координатными осями следующие углы: , , ? РЕШЕНИЕ:
Для направляющих
косинусов выполняется равенство
|
да |
ПП 4. №14 |
Д РЕШЕНИЕ:
Координаты точки
(середины
)
|
7 |
ПП 4. №15 |
Коллинеарны ли
векторы
РЕШЕНИЕ:
Пропорциональность
компонент
|
нет |
ПП 4.5. Скалярное произведение векторов |
||
ПП 4. №16 |
Найдите а)
РЕШЕНИЕ:
а)
|
а)
|
ПП 4 . №17 |
Найдите
РЕШЕНИЕ:
|
|
ПП 4. №18 |
Найдите косинус
угла между векторами
и
,
если
РЕШЕНИЕ:
|
-1 |
ПП 4. №19 |
Вычислите синус
угла, образованного векторами
РЕШЕНИЕ: Найдем косинус нужного угла:
Так как угол между
векторами
|
|
ПП 4. №20 |
Для вектора
РЕШЕНИЕ: Найдем проекцию вектора на орт :
в плоскости
и
лежит составляющая
|
|
|
ПП 4. №21 |
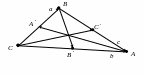
Покажите, что сумма квадратов медиан треугольника относится к сумме квадратов его сторон, как 3:4. РЕШЕНИЕ:
П
Осталось найти требуемое отношение:
|
||
ПП 4. №22 |
П РЕШЕНИЕ:
|
|
ПП 4. №23 |
Докажите, что вектор
РЕШЕНИЕ:
|
|
ПП 4. №24 |
Д Доказательство:
а) Рассмотрим
треугольник
,
построенный на векторах
Пусть третья сторона
Теорема косинусов доказана.
б) При
|
|
ПП 4. №25 |
Д РЕШЕНИЕ:
Пусть
|
|

 адан
тетраэдр
адан
тетраэдр
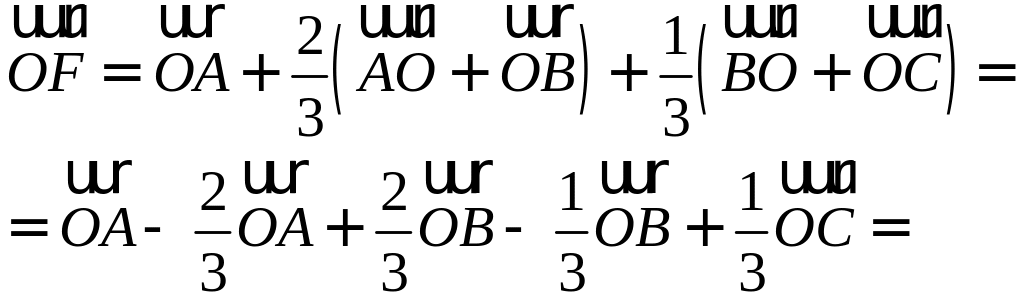
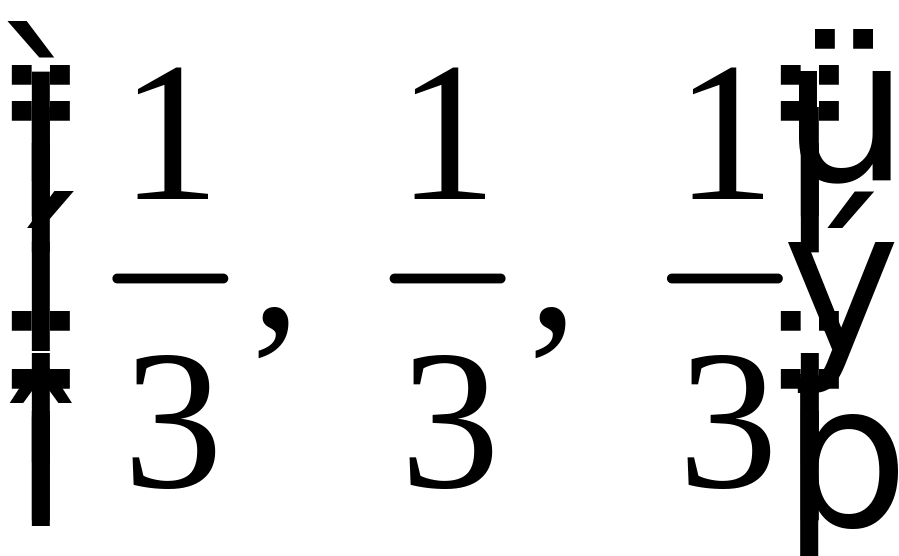 .
. пространстве заданы треугольники
и
пространстве заданы треугольники
и
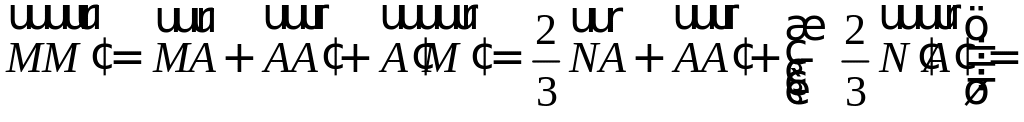
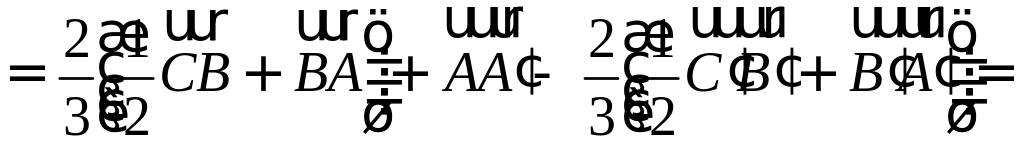
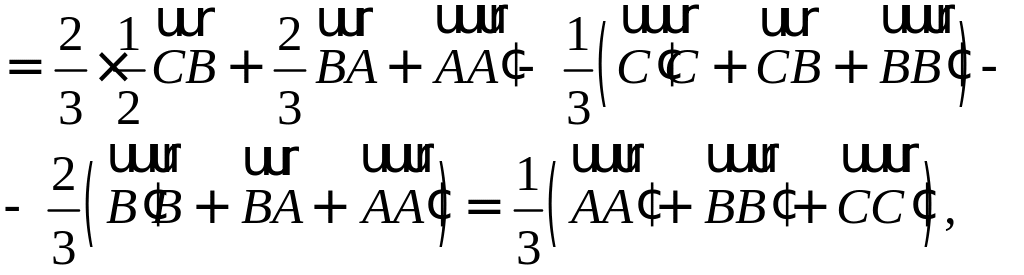
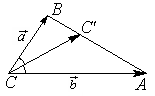 треугольнике
разложите биссектрису
по базису векторов
треугольнике
разложите биссектрису
по базису векторов
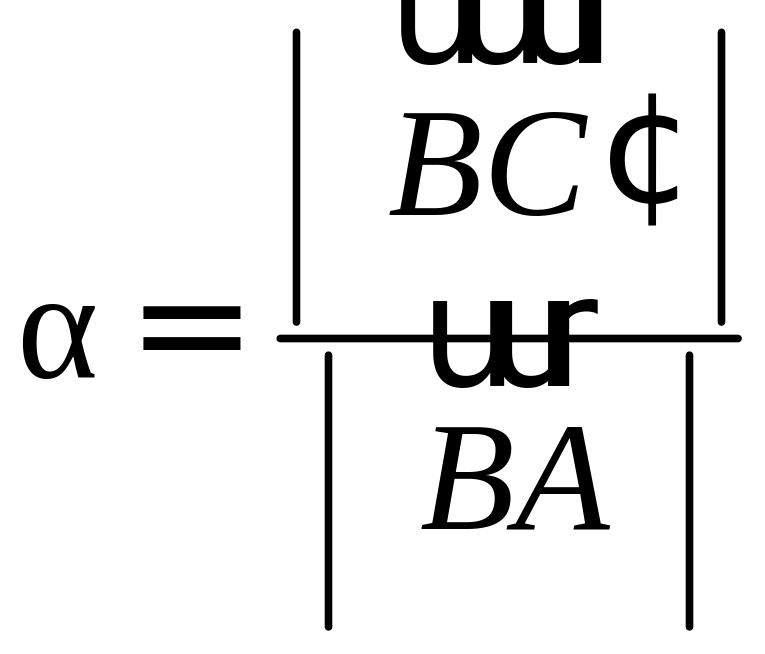 .
.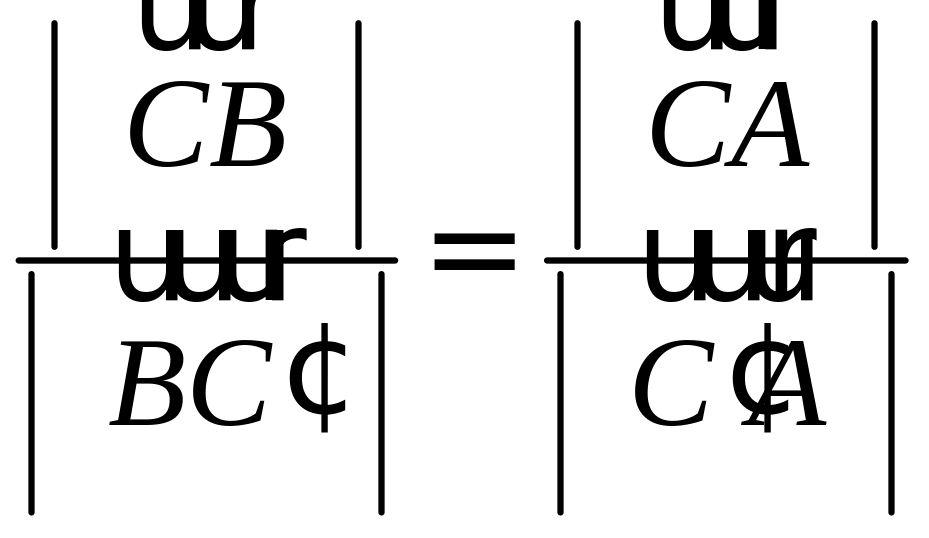 и
тем, что
и
тем, что
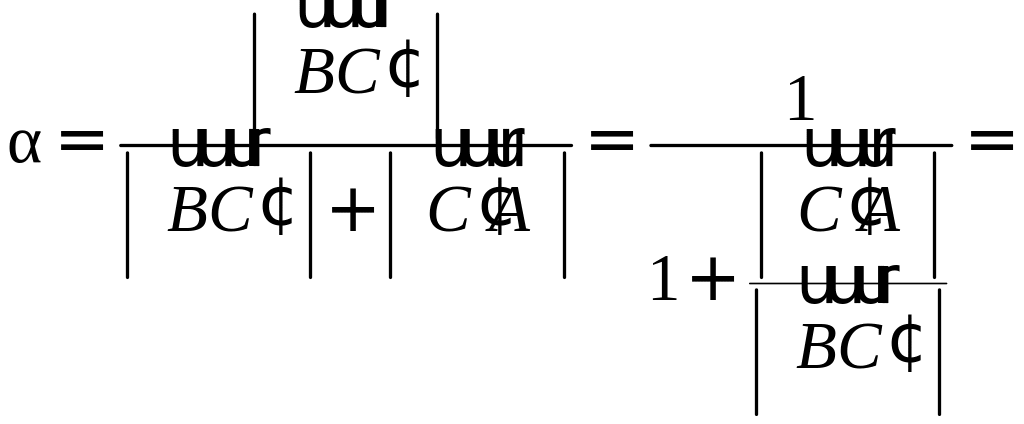
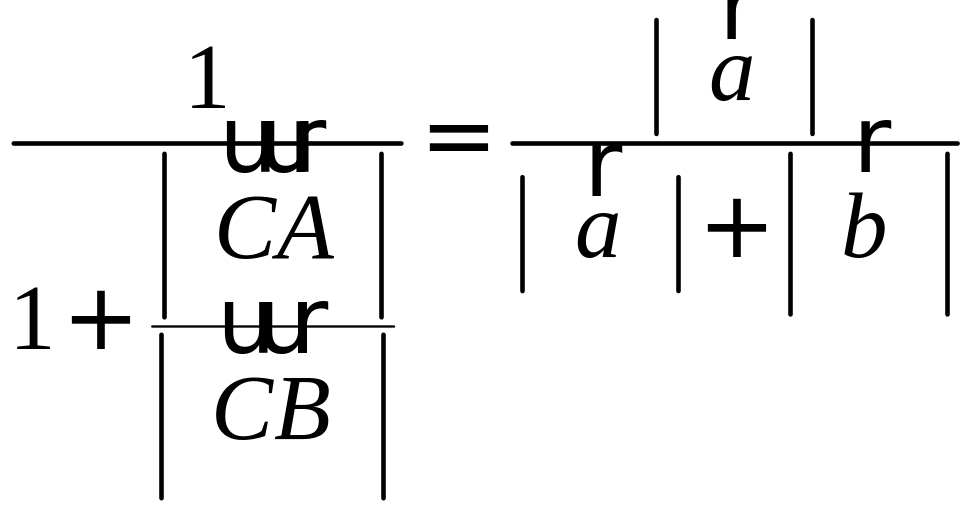 .
Итак,
.
Итак,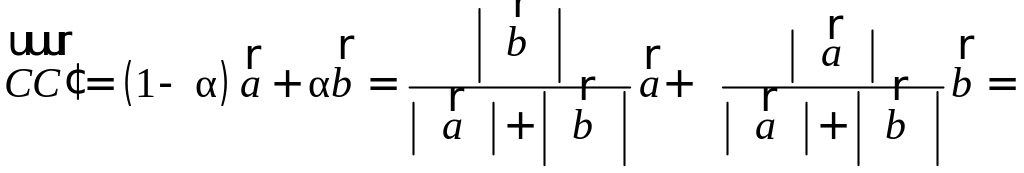
 бозначим
бозначим
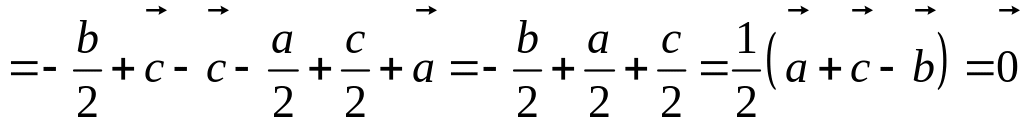 .
.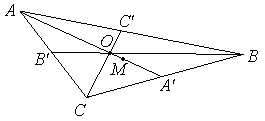 окажите,
что точка пересечения медиан треугольника
делит каждую медиану в отношении
окажите,
что точка пересечения медиан треугольника
делит каждую медиану в отношении
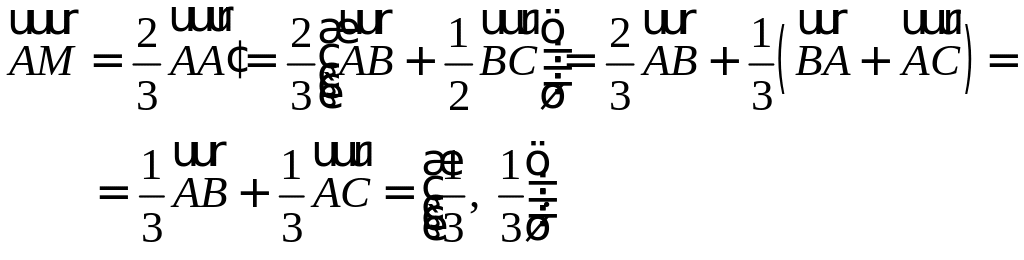
 очки
очки
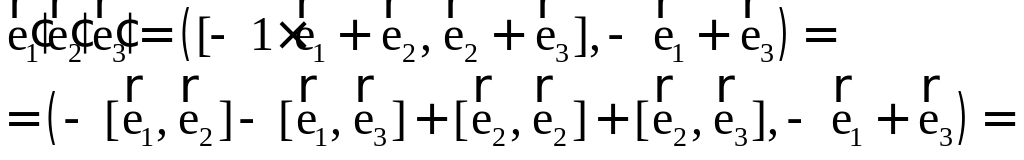
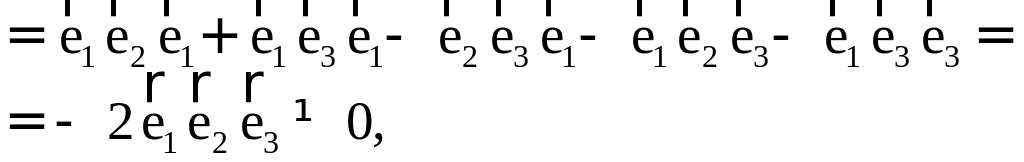
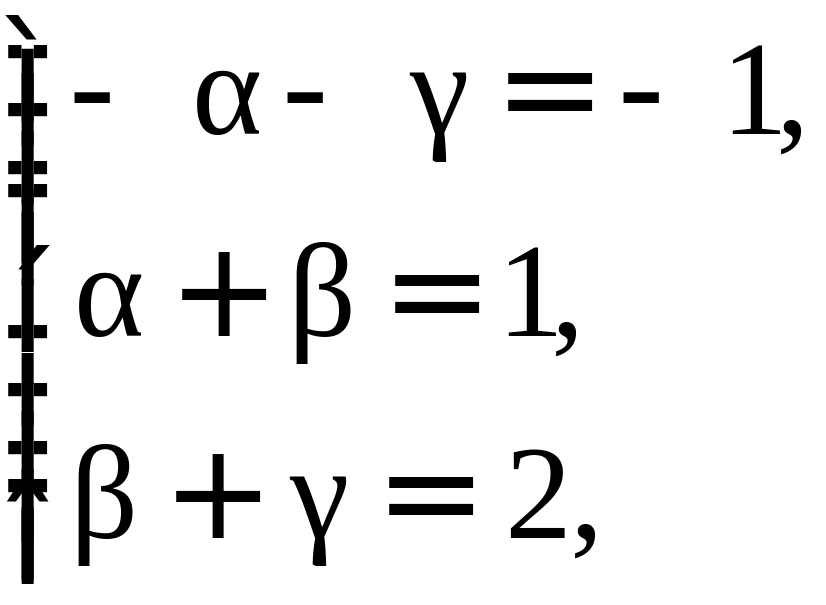
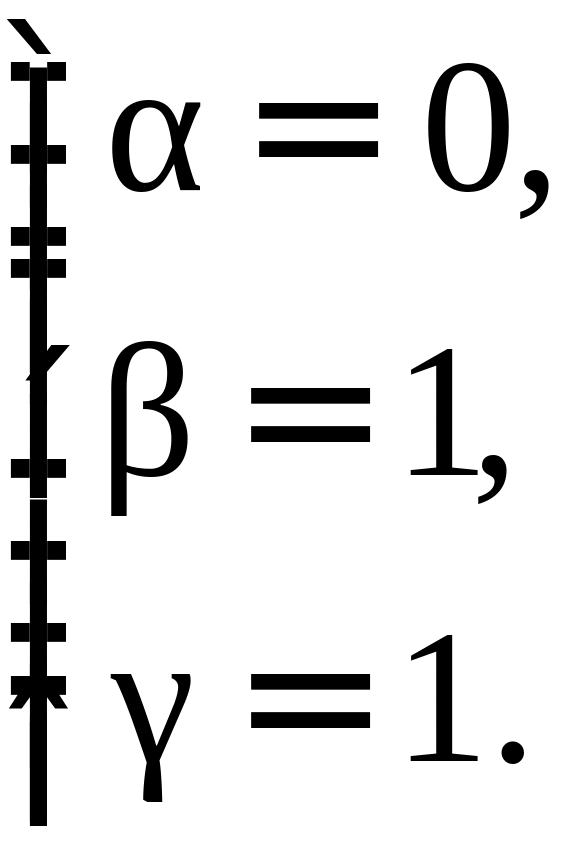
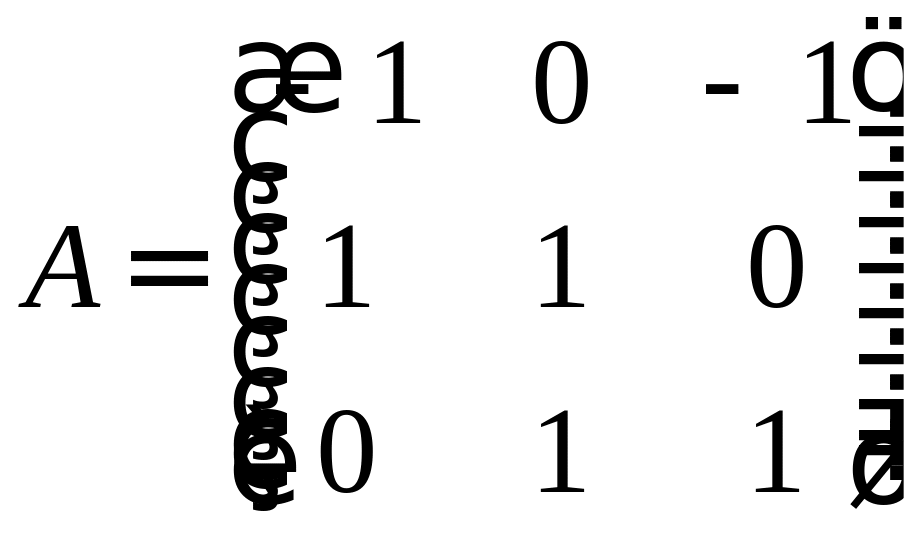 ,
,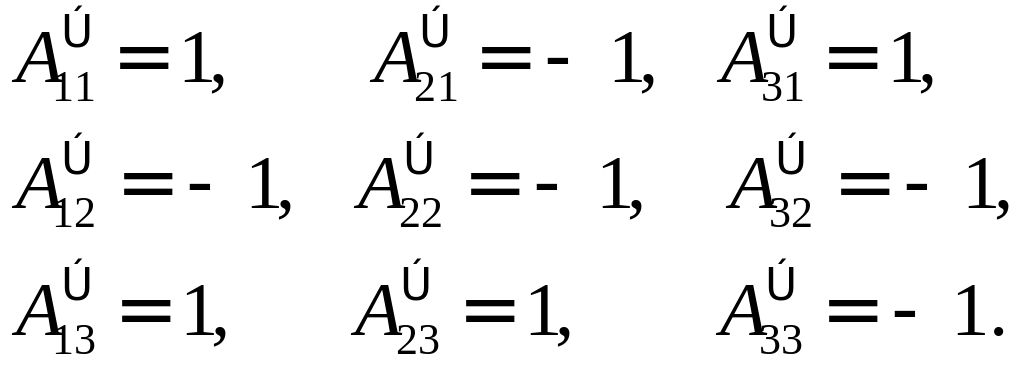
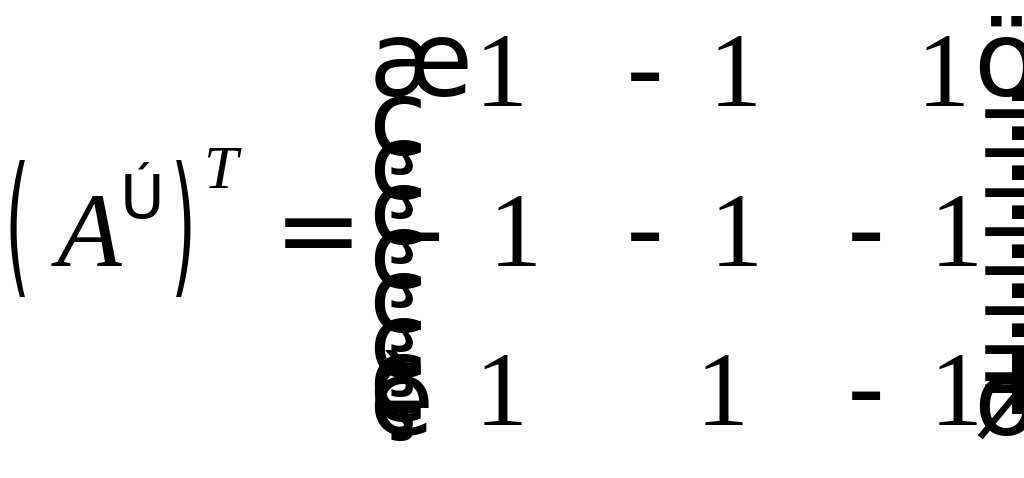 ,
,
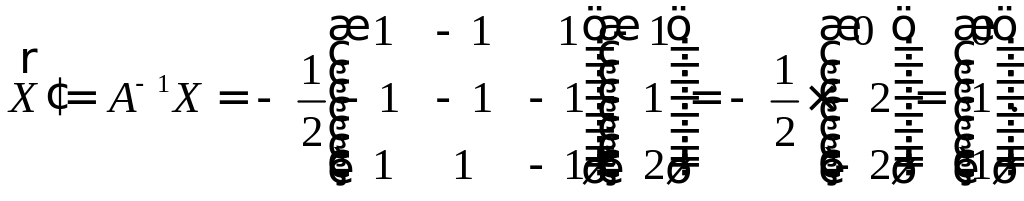
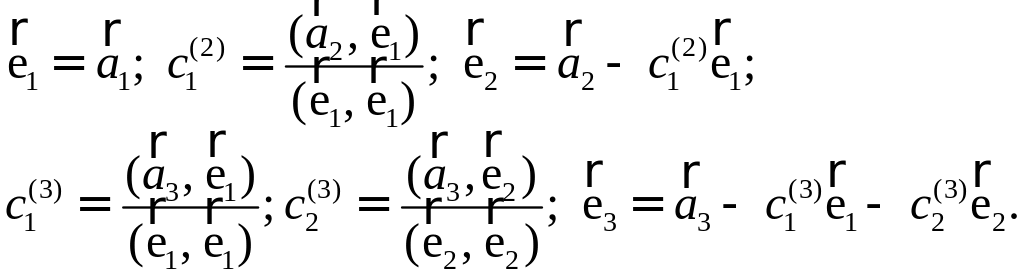
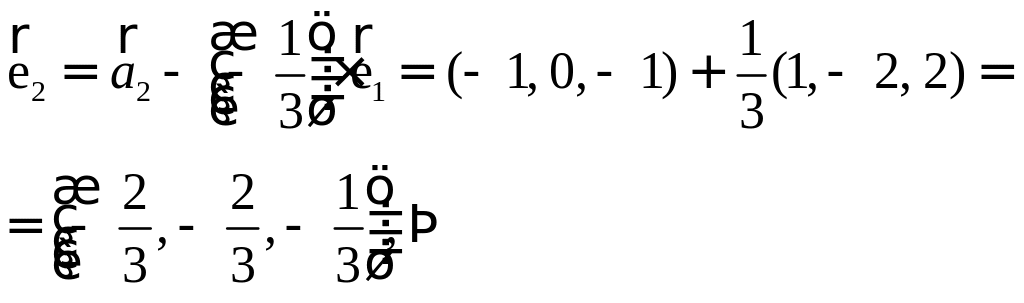
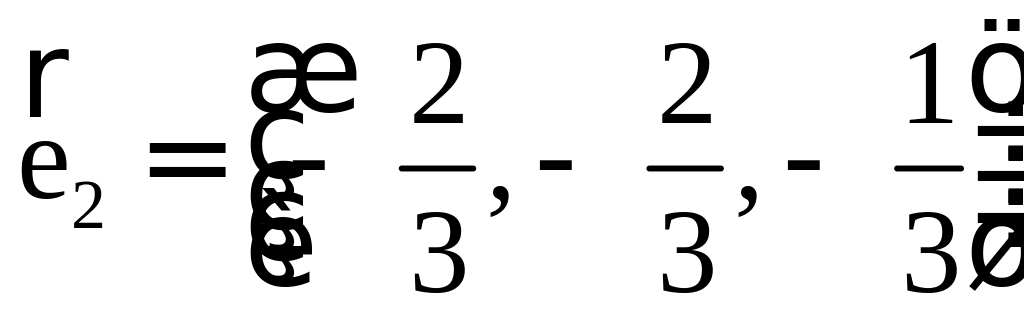 .
.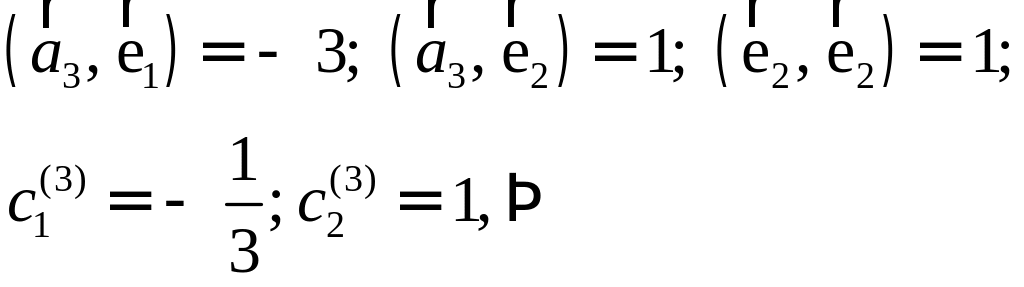
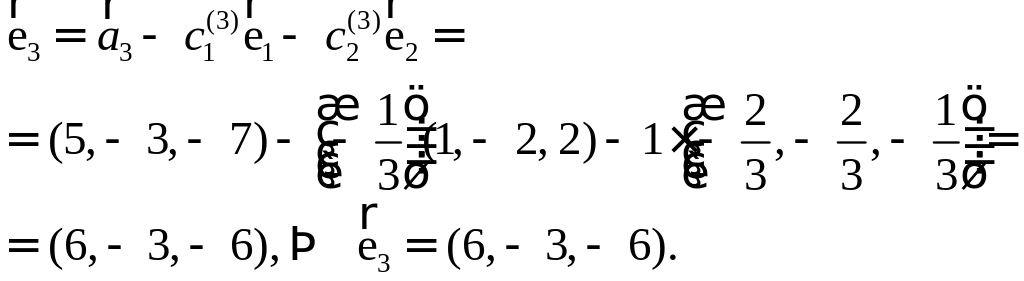
 ,
,
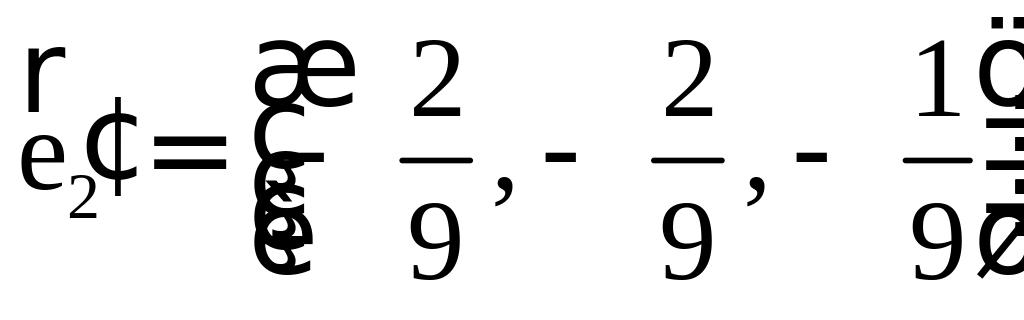 ,
,
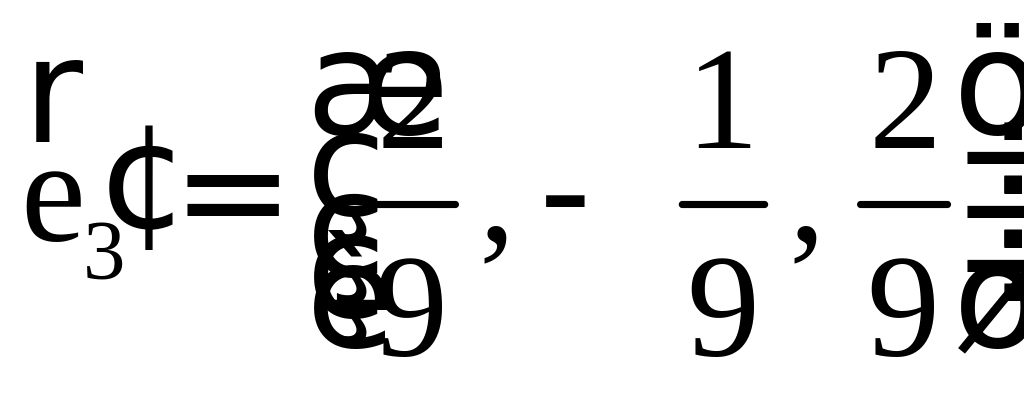 .
.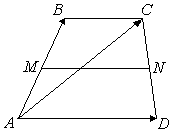 трапеции
с основаниями
и
известны векторы
трапеции
с основаниями
и
известны векторы
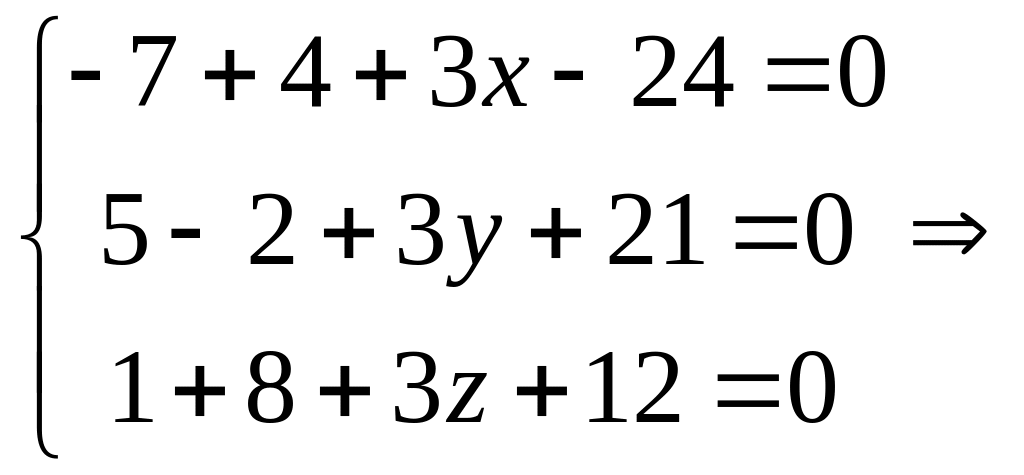
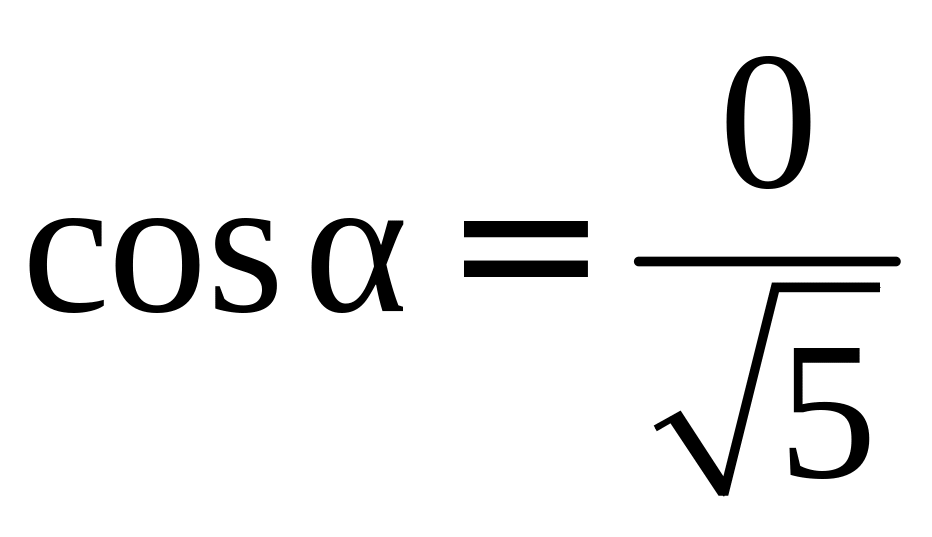 ;
;
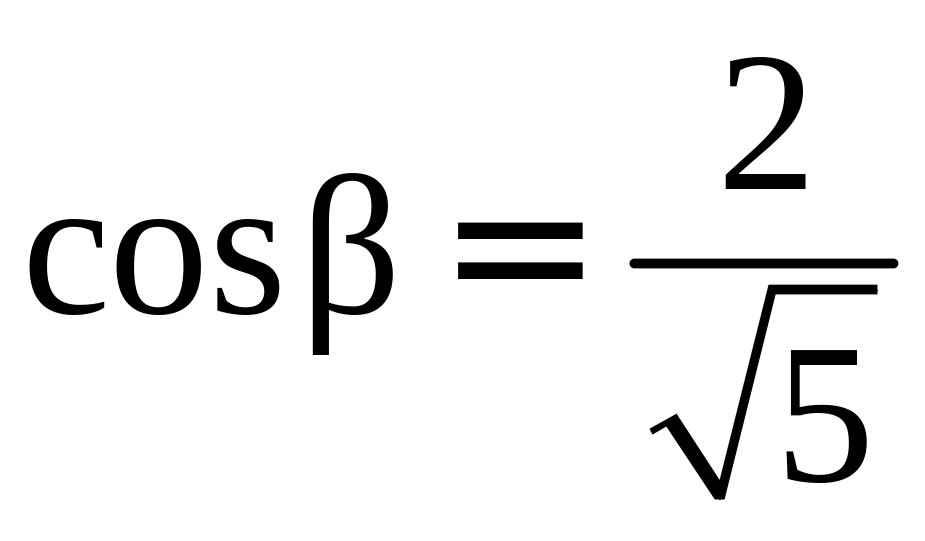 ;
;
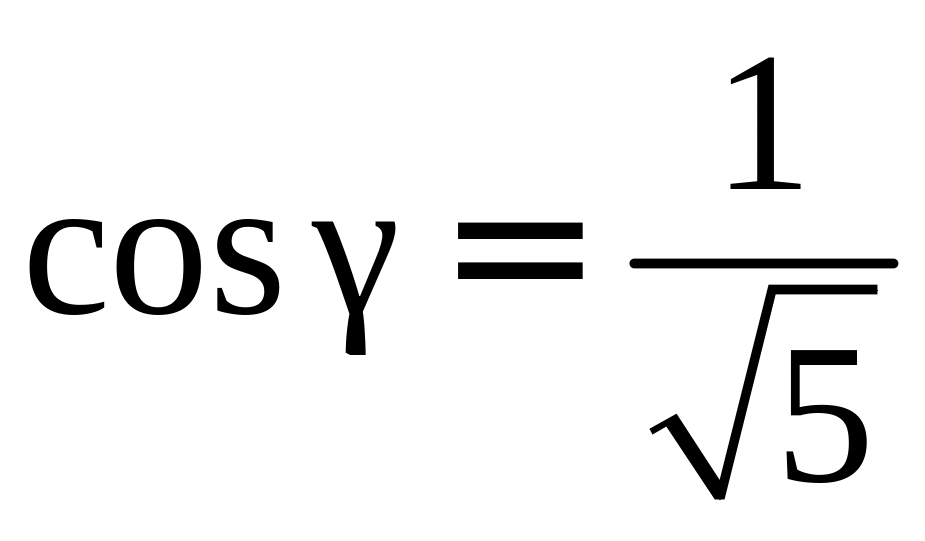 .
.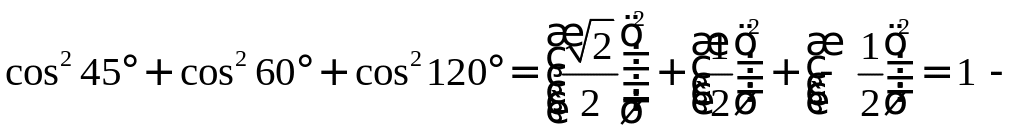 равенство
выполняется.
равенство
выполняется.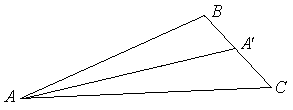 аны
точки
аны
точки
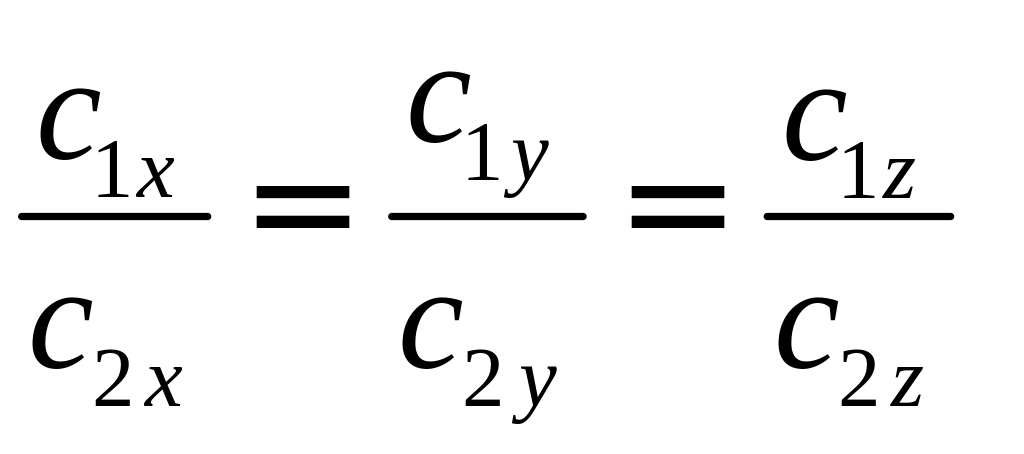 не выполняется, векторы неколлинеарны.
не выполняется, векторы неколлинеарны.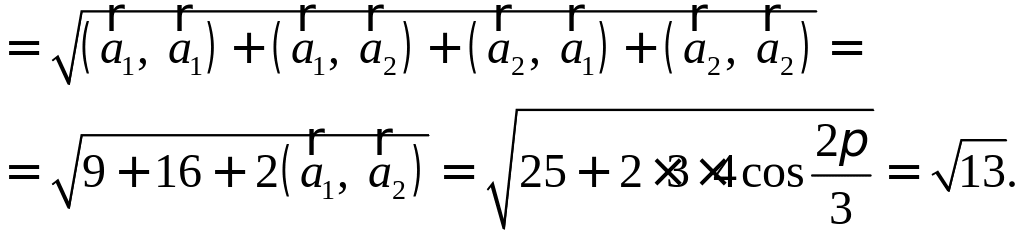
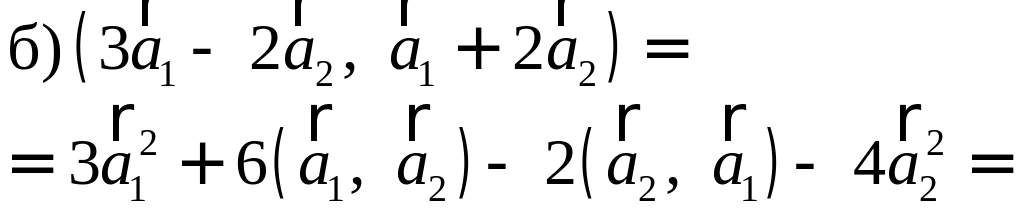
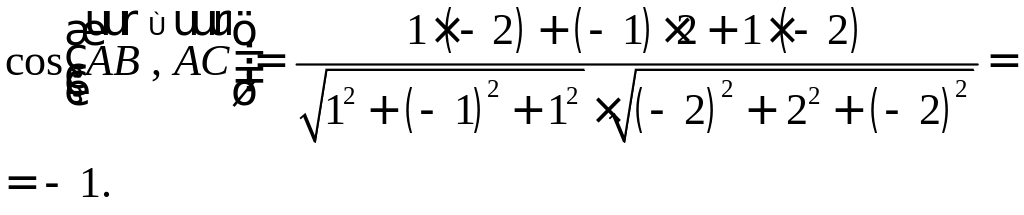
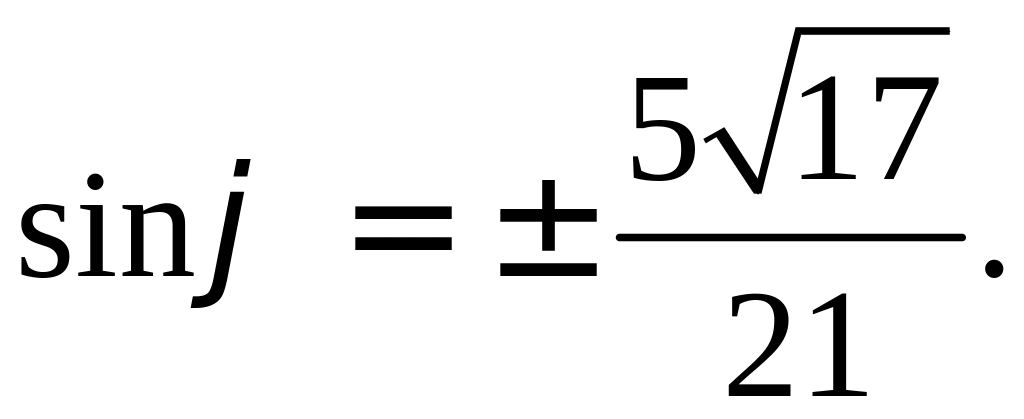
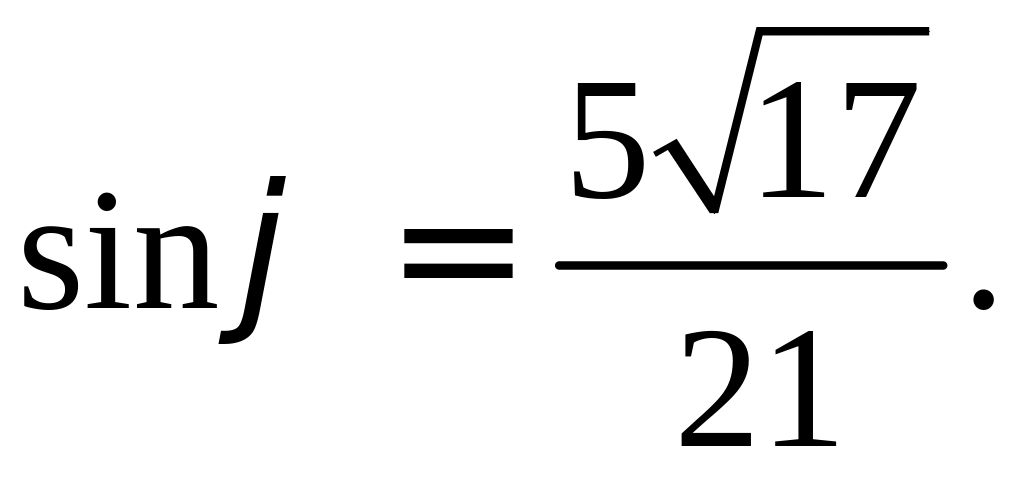
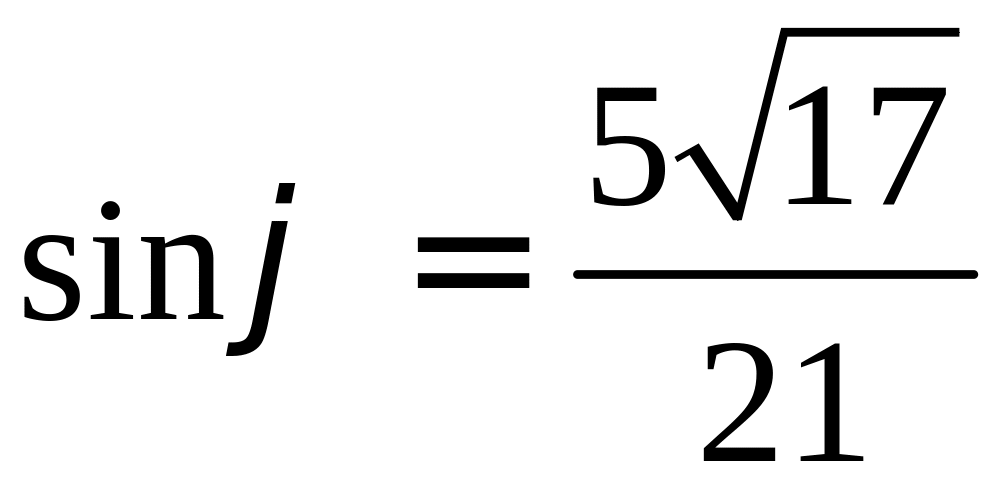 .
.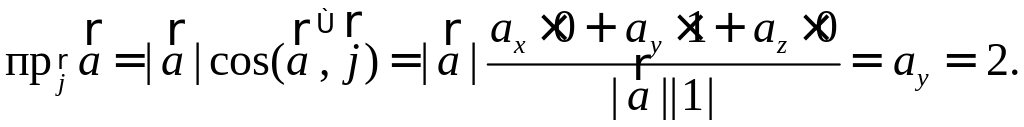 Таким
образом, ортогональная составляющая
вектора
вдоль
равна
Таким
образом, ортогональная составляющая
вектора
вдоль
равна
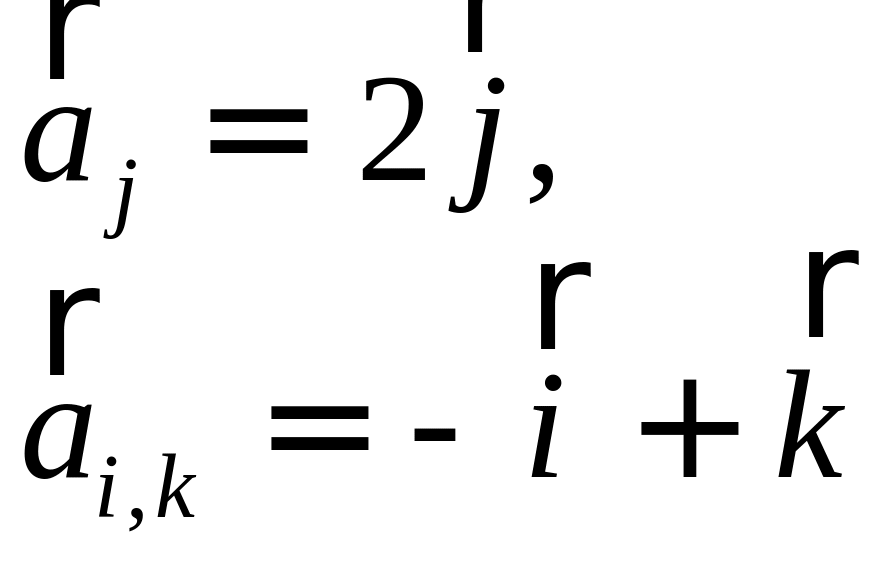
 усть
усть
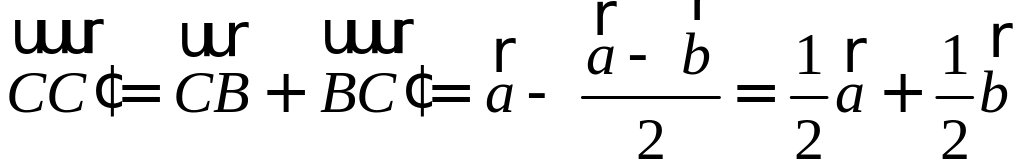 ,
,
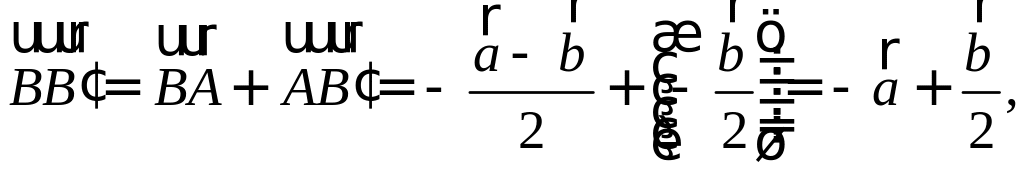
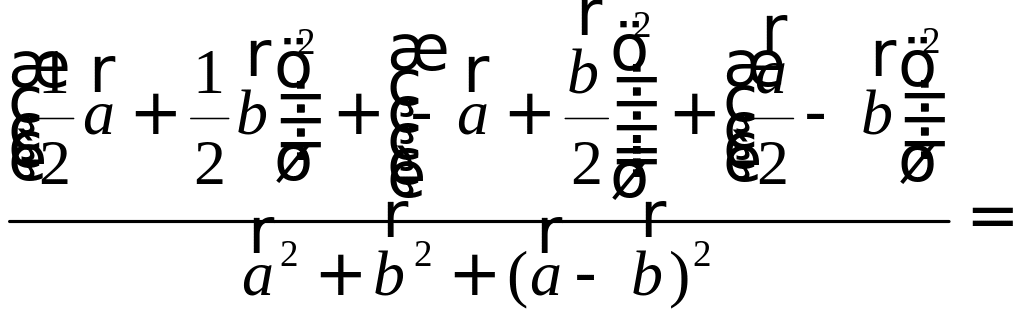
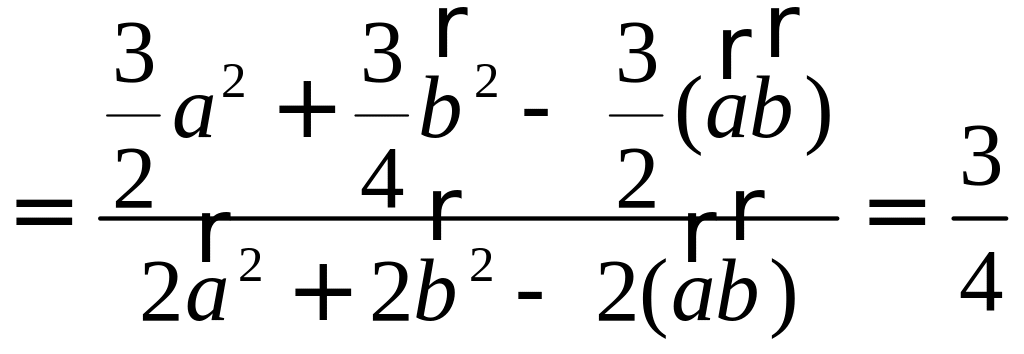
 окажите,
что четырехугольник
ромб, если
окажите,
что четырехугольник
ромб, если
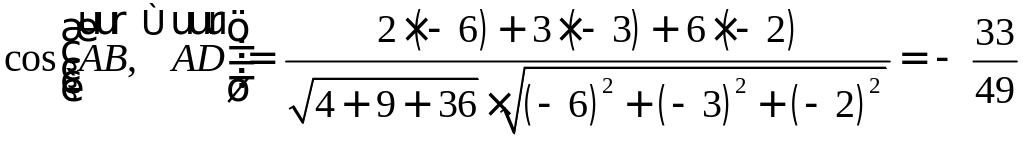 ,
,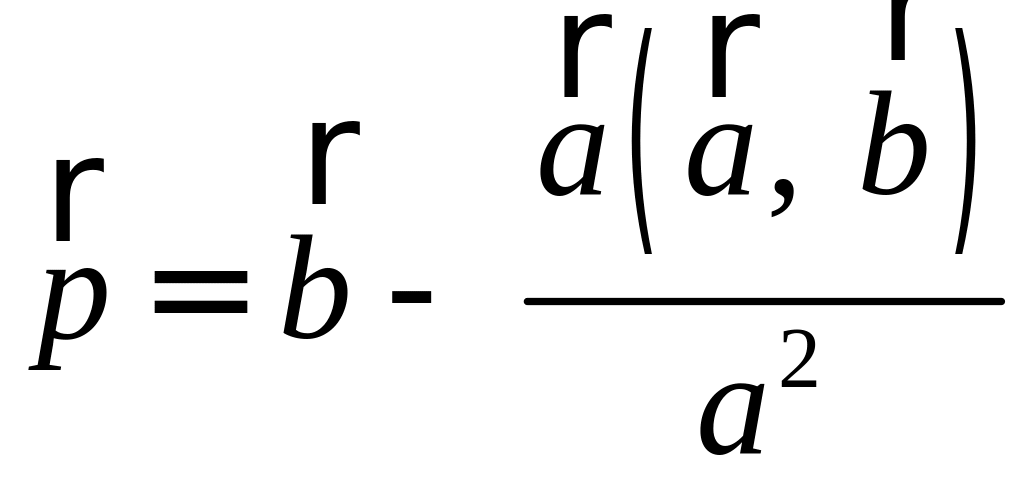 перпендикулярен вектору
.
перпендикулярен вектору
.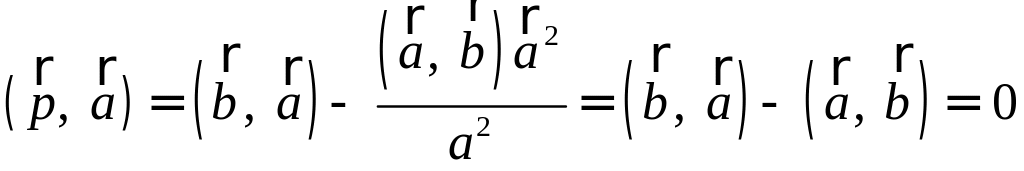 .
.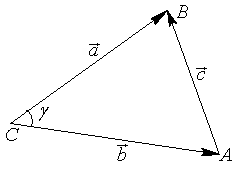 окажите:
а) теорему косинусов; б) теорему
Пифагора.
окажите:
а) теорему косинусов; б) теорему
Пифагора.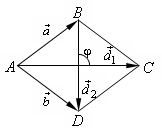 окажите,
что диагонали ромба взаимно
перпендикулярны.
окажите,
что диагонали ромба взаимно
перпендикулярны.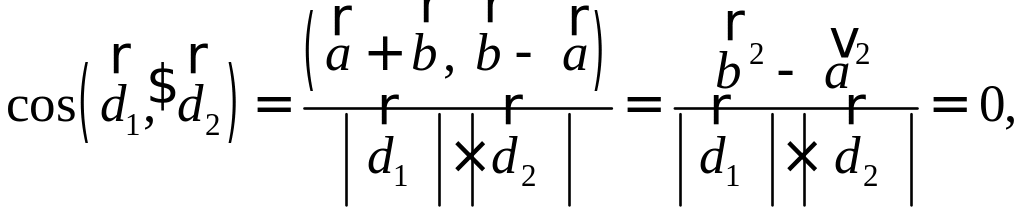 так как для ромба
так как для ромба