3.3.3 Шеститочечная параметрическая схема
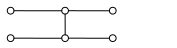
Сеточный шаблон показан на рис. 3.6:
Рис. 3.6 Сеточный шаблон шеститочечной параметрической схемы
Разностная схема:
,
,
,
,
.
где
— параметр схемы;
— явная четырехточечная
схема;
— неявная
четырехточечная схема;
— схема
Кранка-Николсона.
Метод решения полученной системы линейных уравнений с матрицей трехдиагональной структуры — прогонка.
Порядок аппроксимации:
:
,
:
,
:
.
Введем обозначения
,
.
Схема устойчива
при любых
,
если
;
при схема устойчива, если
.
3.3.4 Схема Франкела-Дюфорта
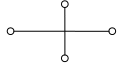
Сеточный шаблон показан на рис. 3.7:
Рис. 3.7 Сеточный шаблон
Разностная схема:
,
,
,
,
.
Значения функции
на втором слое по времени рассчитываются
по явной центральной четырехточечной
схеме. Значение сеточной функции на
верхнем временном слое
рассчитывается по ее значениям на двух
предыдущих нижних слоях:
и
.
Порядок аппроксимации:
.
Схема устойчива
при любых
,
.
3.3.5 Схема Ричардсона
Сеточный шаблон показан на рис. 3.8:
Рис. 3.8 Сеточный шаблон
Разностная схема:
,
,
,
, .
Значения функции на втором слое по времени рассчитываются по явной центральной четырехточечной схеме. Значение сеточной функции на верхнем временном слое рассчитывается по ее значениям на двух предыдущих нижних слоях: и .
Порядок аппроксимации:
Схема неустойчива при любых .
3.3.6 Схема Алена-Чена
Сеточный шаблон показан на рис. 3.9:
Рис. 3.9 Сеточный шаблон
Разностная схема:
,
,
,
, .
Значения сеточной
функции на верхнем временном слое
находятся по ее значениям на нижнем
слое, поскольку разностное уравнение
разрешается относительно
.
Порядок аппроксимации:
.
Схема устойчива при любых .
3.3.7 Нецентральная явная схема
Сеточный шаблон показан на рис. 3.10:
Рис. 3.10 Сеточный шаблон
Разностная схема:
,
,
,
, .
Значение сеточной
функции на верхнем временном временном
слое
рассчитывается по ее значениям на нижнем
слое
(значения сеточной функции в точках {
;
}
рассчитываются по шеститочечной
параметрической схеме при
).
Порядок аппроксимации:
.
Схема устойчива при любых .
3.3.8 Схема Саульева
Сеточный шаблон показан на рис. 3.11:
Рис. 3.11 Сеточный шаблон
Разностная схема:
,
,
начальные и граничные условия в такой схеме реализуют следующим образом:
,
,
, .
Алгоритм численного решения задачи — «бегущий счет»: слева направо — первый этап, справа налево — второй.
Порядок аппроксимации: /
Схема устойчива при любых К.
3.3.9 Точечные решения тестовых краевых задач для одномерного линейного уравнения теплопроводности
В дальнейшем мы будем сравнивать численные решения с точными решениями следующих задач.
Задача 1:
,
,
,
,
,
,
,
,
.
Точное решение:
.
Задача 2:
, , ,
,
,
, ,
,
.
Точное решение:
.
Задача 3:
,
,
,
,
,
, ,
, .
Точное решение:
.