15

Лекции

«ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ,

ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧАХ»

(Часть IV: Численные квадратуры)

Новочеркасск 2012

Содержание

СОДЕРЖАНИЕ 3

4. Численные квадратуры 4

4.1. Введение 4

4.2. Одномерные квадратурные правила и формулы 4

4.3. Формулы прямоугольников 4

4.4. Формула трапеций 5

4.5. Метод Ньютона-Котесса 6

4.6. Формула Симпсона (метод парабол) 6

4.7. Формула Ньютона-Котесса при n=4 (формула Бодэ) 8

4.8. Формула Уэддля (Веддля) 8

4.9. Формула Ньютона-Котесса (n=6) 8

4.10. Метод Чебышева 9

4.11. Метод Гаусса 9

4.12. Переход от одного отрезка к другому 10

4.13. Квадратурные правила Гаусса-Кронрода 11

4.14. Интегрирование таблично заданных функций 13

4.15. Эрмитова кубическая квадратура 14

4.16. Двойные и тройные интегралы 14

ЛИТЕРАТУРА 15

4. Численные квадратуры

4.1. Введение

Этот раздел посвящён решению следующей задачи: вычислить интеграл

.

Это одна из фундаментальных задач математического анализа. Она тесно связана с задачей решения дифференциальных уравнений.

4.2. Одномерные квадратурные правила и формулы

Обычно аппаратом, используемым для построения квадратур, является аппарат интерполирования. Вместо того, чтобы вычислить непосредственно, сперва вычисляют значения функции в заданных точках . Пусть - интерполяционный полином, проходящий через точки . Тогда, если , то и . Поскольку интерполирование полинома не составляет труда, а аппарат интерполирования вполне доступен, такой подход представляется численно реализуемым и эффективным.

Получим простейшие квадратурные формулы. Для этого введём терминологию , которой в дальнейшем будем пользоваться. Назовём -точечной квадратурной формулой равенство .

При этом называются весами, а - узлами квадратурной формулы, - остатком или погрешностью. Веса и узлы зависят от , но не зависят от . Сумму в правой части, которую можно рассматривать как приближение к , часто называют квадратурным правилом. Чтобы приближенно вычислить интеграл, мы вычисляем только квадратурное правило, так как остаток обычно содержит выражение нам недоступные (производные подынтегральной функции). Важное свойство наших формул – их линейность. Это означает, что правило, дающее приближение к интегралу от , можно получить сложением правил, дающих приближение к и .

4.3. Формулы прямоугольников

Простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию на интервале интегрирования заменяем полиномом нулевой степени, т. е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке интервала интегрирования. Приближенное значение интеграла определится как площадь прямругольника, одна из сторон которого есть длина отрезка интегрирования, а другая – аппроксимирующая константа. Отсюда происходит и название методов.

Наименьшую погрешность из методов прямоугольников имеет метод средних прямоугольников, когда константу берём равной значению в средней точке интервала (Рис.1 а).

Методы левых (Рис.1 б) и правых (Рис.1 в) прямоугольников, заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно невысокую точность.

Для метода средних прямоугольников

где - значение второй производной в точке , где она максимальна, - шаг интегрирования, - количество отрезков разбиения.

Для метода левых прямоугольников

.

Для метода правых прямоугольников

.

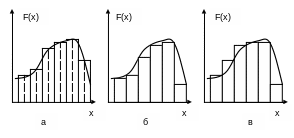
Рис. 1. Методы средних (а), левых (б) и правых (в) прямоугольников.

Для метода прямоугольников на отрезке интегрирования.