
- •§1. Учет погрешностей вычислений.
- •§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности)
- •§3. Приближенные вычисления без учета погрешностей.
- •§4. Связь между числом количества верных цифр и относительной погрешностью.
- •§5. Прямая задача теории погрешностей (функции от приближенных значений аргументов).
- •§6. Обратная задача теории погрешностей.
- •Принцип равных влияний
- •§7. Метод границ.
- •§8. Математические модели и численные методы.
- •§9. Понятие корректно поставленной и некорректно поставленной задач.
- •§10. Вспомогательные сведения из функционального анализа.
- •§11. Решение уравнений с одним неизвестным. Дихотомия.
- •§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений.
- •По соседним приближениям
- •По невязке
- •§13. Метод Ньютона. Решение уравнений с одной переменной.
- •§14. Метод хорд. Метод секущих.
- •§15. Метод Гаусса решения систем уравнений.
- •§16. Метод квадратного корня.
- •Литература
Лекции
«ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ,
ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧАХ»
(Часть VIII: оценка погрешностей)
Новочеркасск 2012
Оглавление
§1. Учет погрешностей вычислений. 3
§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности) 5
§3. Приближенные вычисления без учета погрешностей. 6
§4. Связь между числом количества верных цифр 7
и относительной погрешностью. 7
§5. Прямая задача теории погрешностей 9
(функции от приближенных значений аргументов). 9
§6. Обратная задача теории погрешностей. 11
§7. Метод границ. 13
§8. Математические модели и численные методы. 15
§9. Понятие корректно поставленной 16
и некорректно поставленной задач. 16
§10. Вспомогательные сведения из функционального анализа. 17
§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений. 20
§13. Метод Ньютона. Решение уравнений с одной переменной. 22
§14. Метод хорд. Метод секущих. 25
§15. Метод Гаусса решения систем уравнений. 27
§16. Метод квадратного корня. 28
ЛИТЕРАТУРА 30
§1. Учет погрешностей вычислений.
При решении математических задач могут возникнуть погрешности по различным причинам:
При составлении математической модели физического процесса или явления приходится принимать условия, упрощающие постановку задачи. Поэтому математическая модель не отражает реальный процесс, а дает его идеализированную картину. Погрешность, возникающая при этом, называется погрешностью постановки задачи.
Часто приходится для решения задачи применять приближенный метод (интеграл заменяют квадратурной суммой, производную заменяют разностью, функцию – многочленом). Погрешность, возникающая при этом, называется погрешностью метода.
Часто исходные данные заданы не точно, а приближенно. При выполнении вычислений погрешность исходных данных в некоторой степени переходит в погрешность результата. Такая погрешность называется погрешностью действий.
Погрешность, возникающая при округлении бесконечных и конечных десятичных чисел, имеющих большее число десятичных знаков, чем надо в округлении, называется погрешностью округления.
Определение.
Пусть х – некоторое число, число а
называется его приближенным
значением,
если а в определенном смысле мало
отличается от х и заменяет х в вычислениях,
 .
.
Определение.
Погрешностью
 приближенного значения а числа х
называется разность
приближенного значения а числа х
называется разность
 ,
а модуль этой погрешностью называется
абсолютной
погрешностью.
,
а модуль этой погрешностью называется
абсолютной
погрешностью.
Если
 ,
то а взято с недостатком.
,
то а взято с недостатком.
Если
 ,
то а взято с избытком.
,
то а взято с избытком.
Определение.
Границей
погрешности приближенного значения а
числа х называется
всякое неотрицательное число
 ,
которое не меньше модуля погрешности:
,
которое не меньше модуля погрешности:
 .
.
Говорят,
что приближение а приближает число х с
точностью до
,
если
 ,
,
 ,
,
 .
.
Пример. Пусть а=0,273 – приближенное значение х с точность до 0,001. Указать границы, в которых заключается х.

При округлении чисел считают, что границы погрешности округления равна половине единицы округляемого разряда:
 ,
α – порядок округления разряда.
,
α – порядок округления разряда.
Определение. Относительной погрешностью приближенного значения а числа х называется отношение
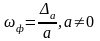 .
.
Пример. Округлить до десятых число 27,52 и найти погрешность и относительную погрешность округления:
 ,
,
 ,
,
 .
.
Также как и абсолютная погрешность относительная погрешность не всегда может быть вычислена и приходится оценивать ее модуль. Модуль относительной погрешности выражается в процентах. Чем меньше модуль относительной погрешности, тем выше качество приближения.
Определение.
Границей
относительной погрешности приближенного
значения а числа х
называется всякое неотрицательное
число
 ,
которое не меньше модуля относительной
погрешности:
,
которое не меньше модуля относительной
погрешности:
 .
.
Установим связь между границами погрешностей абсолютной и относительной:
 - граница относительной
погрешности;
- граница относительной
погрешности;
 - граница абсолютной
погрешности.
- граница абсолютной
погрешности.
 .
.
§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности)
Пусть
 ,
где
,
где
 – число с заданными своими приближениями
с точностью до
– число с заданными своими приближениями
с точностью до
 :
:
 .
.
Обозначим
через
 .
.
 ,
где
,
где
 - граница погрешности суммы приближенного
значения
- граница погрешности суммы приближенного
значения
 .
.
Утверждение 1. Сумма границ погрешностей приближенных слагаемых является границей погрешности их алгебраической суммы.
Доказательство:
 .
.
ЧТД.
Утверждение 2. Среди границ относительной погрешности суммы приближенных слагаемых существует такая, которая не превосходит наибольшей из границ относительной погрешности слагаемых:

.
Утверждение 3. Сумма границ относительных погрешностей сомножителей является границей относительной погрешности их произведения:
 .
.
Следствие
1. При
умножении приближенных значений числа
на точный множитель к, граница относительной
погрешности не меняется, а граница
абсолютной погрешности увеличивается
в
 раз.
раз.
Следствие
2. Произведение
границы относительной погрешности
приближенного значения а числа х на
 является границей относительной
погрешности результата возведения
числа а в целую положительную степень
n:
является границей относительной
погрешности результата возведения
числа а в целую положительную степень
n:
 .
.
Следствие 3. Частное границы относительной погрешности приближенного значения а числа х и n является границей относительной погрешности корня n-й степени из а:
 .
.
Следствие 4. Сумма границ относительных погрешностей приближенных значений делимого и делителя является границей относительной погрешности частного.
