Тема 5. Цілочислові задачі лінійного програмування

Тема 6. Елементи нелінійного програмування

Лекція 6.

Тема лекції: Задачі нелінійного програмування

Мета: ознайомити студентів з методами розв’язання задач цілочислового програмування методом Гоморі та з основними методами розв’язування задач нелінійного програмування.

План лекції

1. Задачі дробово-лінійного програмування.

2. Задачі цілочислового програмування.

3. Класичні методи розв’язування задач нелінійного програмування.

4. Метод множників Лагранжа.

5. Задачі опуклого прогрмування.

Література:

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.

2. Іванюта І.Д. Практикум з математичного програмування: Навчальний посібник/ І.Д. Іванюта, В.І. Рибалка, І.А. Рудоміра – Дусятська. – К. : «Слово», 2008. – 296 с.

3. Кучма М.І. Математичне програмування: приклади і задачі: Навчальний посібник/ М.І. Кучма. - Львів: «Новий Світ - 2000», 2006. – 344 с.

4. А. Черемис, Р. Юринець, О. Мищишин. Методи оптимізації в економіці. Навчальний посібник. – К.: Центр навчальної літератури, 2006. – 152 с.

1. Задачі дробово-лінійного програмування.

Математична модель задачі дробово-лінійного програмування записується так:

Z=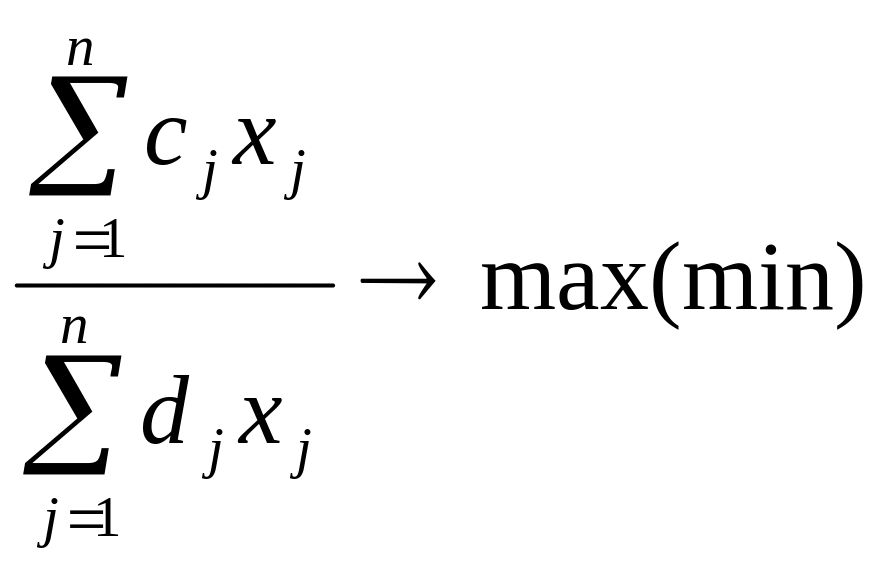 (1)

за умов

(2)

x_ij≥0, (j= ), (3)

де c_j, d_j, b_i, a_ij, (j= ), (i= ) – сталі величини, 0.

Умови обмежень (1) – (3) даної задачі є лінійними, тому ОДР є опуклою множиною, і цільова функція (1) досягає екстремального значення в одній з вершин цієї області.

Задачу дробово-лінійного прогамування можна звести до задачі ЛП за попомогою стандартного перетворення до задачі ЛП і розв’язати її симплекс-методом:

y₀=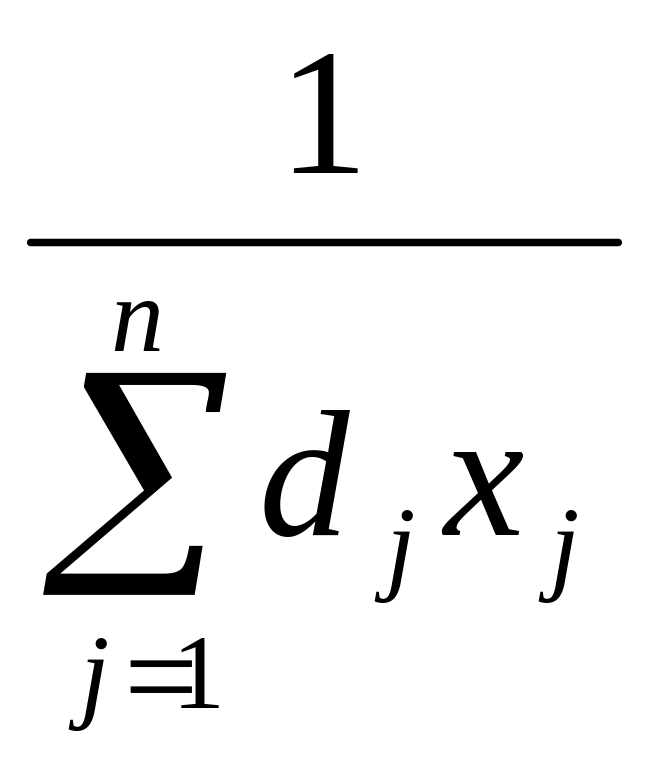

y_i=y₀x_i, i= .

2. Задачі цілочислового програмування.

Задача цілочислового програмування формулюється так:

Z= (4)

за умов

,= b_i, i= , (5)

x_j≥0, (j= ), (6)

x_j - цілі, (j= ), (7)

умова цілочисельності (7), яка додається до звичайної задачі ЛП, суттєво ускладнює її розв’язання.

Метод Гоморі. Сутність методу Гоморі (метод відтинання) полягає у тому, що спочатку розв’язується звичайна задача ЛП без урахування вимог цілочисельності змінних. Якщо отриманий оптимальний план задачі цілочисловий, то задача розв’язана. У протилежному випадку у модель вводиться спеціальне додаткове обмеження, що враховує цілочисельність змінних і володіє такими властивостями;

- вона повинна бути лінійною;

- вона повинна відтинати знайдений оптимальний нецілочисловий план задачі;

- не повинна відтинати ні одного цілочислового плану.

Додаткове обмеження, що має перелічені вище властивості, називається правильним відтинанням.

Це додаткове обмеження вводиться до оптимального плану якщо серед компонент оптимального розв’язку яка має найбільшу дробову частину. На базі цієї змінної будується додаткове обмеження Р.Гоморі:

де - дробова частина числа,

=а-[a].