2.2.2.3. Меры предосторожности в методе Ньютона

Меры предосторожности для метода Ньютона основаны на двух идеях. Во-первых, мы хотим иметь гарантию, что на каждой итерации происходит приближение к решению. Во-вторых, мы хотим предотвратить использование больших шагов, которые могут привести к катастрофе.

Мы хотим добиться выполнения условия

.

Напомним, что вторая (евклидова ) норма .

С целью предотвращения больших шагов наложим ограничение на шаг :

,

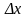где - некоторый ограничитель, выбираемый алгоритмом. Ограничитель выбирает нашу степень доверия к модели . Если модель хорошая, то аппроксимация будет эффективной при больших значениях и можно выбирать большой ограничитель . Если модель плохая, то аппроксимация будет приемлемой лишь при малых значениях и нужно использовать малое значение . Множество называется доверительной областью.

Если ограничитель мал, то трудно надеяться, что решение уравнения Ньютона будет удовлетворять нашему ограничению. Необходим некоторый компромисс. Другими словами необходима задача оптимизации:

Минимизировать по норму при условии .

Опишем простейшую версию всего алгоритма в целом. На -й итерации выполняются следующие действия:

1. Если , то останов.

2. Вычислить шаг , решая приведённую выше задачу оптимизации с ограничением (Минимизировать по норму при условии ).

3. Если , то шаг принимается. Положить . Перейти к шагу 1.

4. Если шаг отвергается, то уменьшить ограничитель . Положить . Перейти к шагу 1.

Невозможно гарантировать, что алгоритмы доверительной области будут сходиться к решению СНАУ. Для задач размерности больше единицы методы с гарантированной глобальной сходимостью всё ещё остаются предметом исследования. Эти проблема тесно связана с задачей глобальной оптимизации.

2.2.2.4. Локальное решение нелинейного уравнения

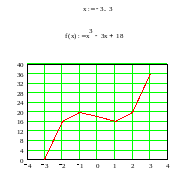
В качестве иллюстрации решения рассмотрим одномерную задачу

.

Решение нелинейного уравнения есть точка . Однако точка является его локальным решением. Чтобы убедиться в этом, заметим, что

.

В точке производные имеют вид

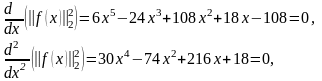
поэтому - локальный минимизатор . Но поскольку , точка не является решением нелинейного уравнения.

Чтобы избежать нахождения только локальных решений, можно использовать более сложные стратегии. К ним относятся методы гомотопии.

2.2.3. Метод Ньютона по параметру

Метод Ньютона по параметру относится к классу квазиньютоновских (градиентных) методов и предусматривает расчет нового исходного приближения по формуле

,

где - (итерационный коэффициент) параметр, выбираемый на каждой итерации.

При метод совпадает с обычным методом Ньютона.

Параметр выбирают с целью ускорения сходимости и предупреждения расхождения метода. Факт расхождения может быть установлен, если невязка любого уравнения системы не уменьшилась по сравнению с предыдущей итерацией .

2.2.4. Метод Бройдена

Метод предусматривает выбор параметра в процессе поиска по направлению вектора поправок минимума одной из норм вектора невязок, например, евклидовой (или второй нормы) . В простейшем случае можно попытаться выполнить последовательность расчетов , уменьшая шаг вдвое, т.е. полагая пока не уменьшится, или не станет малой величиной. Более сложные варианты предусматривают аппроксимацию сечения по направлению поверхности функции невязок выпуклой квадратичной функцией и выбор , обеспечивающего минимум этой функции.

Вычислим значение и, выполнив предварительно шаг метода Ньютона, вычислим 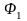. Если , то поиск на отрезке [0,1] начинается с , в противном случае с . Зададимся некоторым 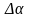и вычислим значения функции 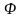в точках в первом случае и в точках во втором случае, где Поиск прекращается при выполнении условия

.

В окрестности -й точки производится квадратичная аппроксимация функции и определяется из условия ее минимума (равенства нулю производной) значение , равное

,

где - точки, в которых известно значение аппроксимируемой функции .