
- •Тема 1. Механічні коливання Основні формули та визначення
- •2. Динаміка гармонічних коливань
- •3. Енергія тіла, що здійснює вільні гармонічні коливання
- •4. Спосіб векторних діаграм – графічне зображення гармонічного руху
- •5. Додавання двох однаково спрямованих гармонічних коливань рівних частот
- •7. Додавання двох взаємно перпендикулярних гармонічних коливань
- •8. Згасаючі (затухаючі) механічні коливання
- •9. Вимушені механічні коливання
- •Задача 1.1
- •Розв’язування 1.1.
- •Задача 1.2
- •Література
Задача 1.1
Написати рівняння гармонічного коливання,
якщо амплітуда коливання дорівнює
![]() м, а частота
м, а частота
![]() Гц.
Гц.
Розв’язування 1.1.
Рівняння гармонічного коливання у загальному вигляді маємо:
![]() (1)
(1)
Для нашого випадку рівняння гармонічного
коливання має вигляд:![]() (2)
(2)
Задача 1.2
Коливання вантажу на пружині масою
![]() кг описується рівнянням
кг описується рівнянням
![]() .
Визначити:
.
Визначити:
Амплітуду коливання
 ;
;Колову частоту ;
Частоту
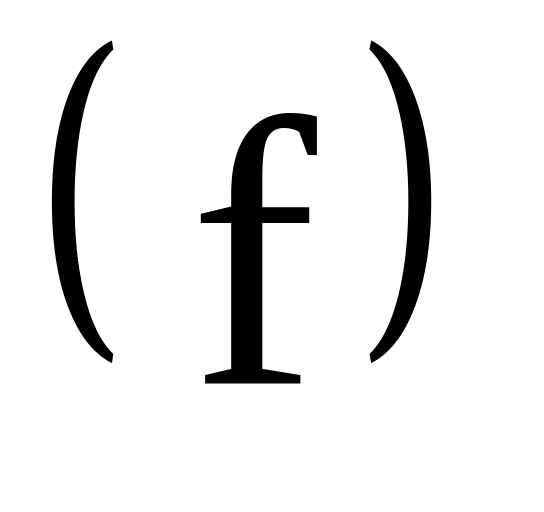 ;
;Період ;
Початкову фазу
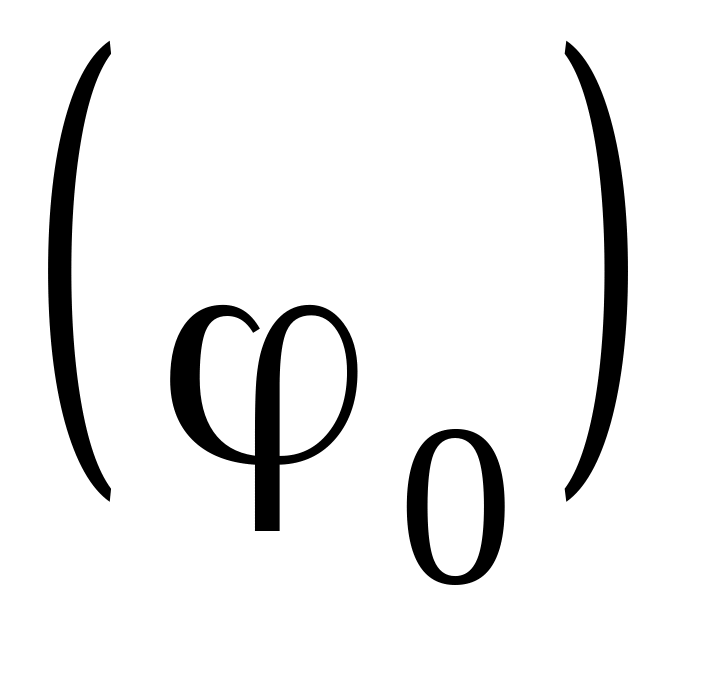 ;
;Повну енергію
 ;
;Максимальну швидкість руху вантажу
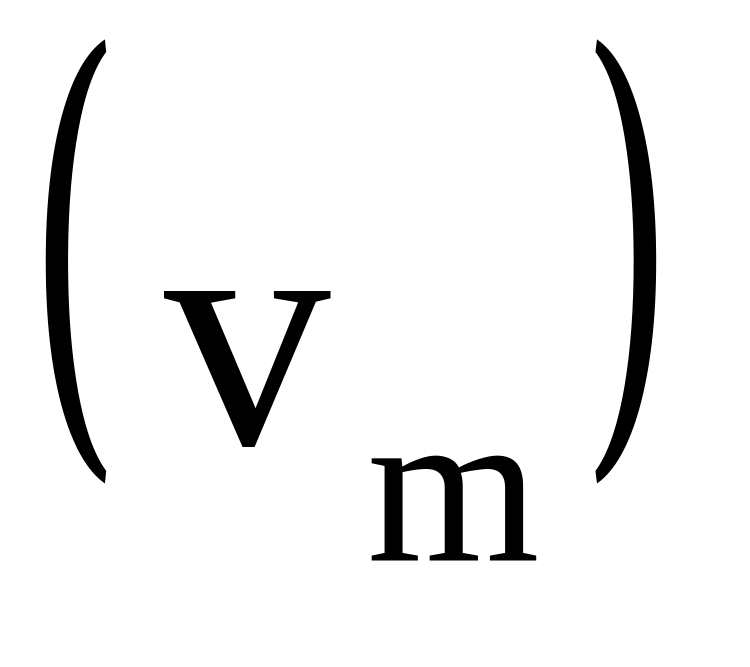 ;
;Коефіцієнт жорсткості пружини
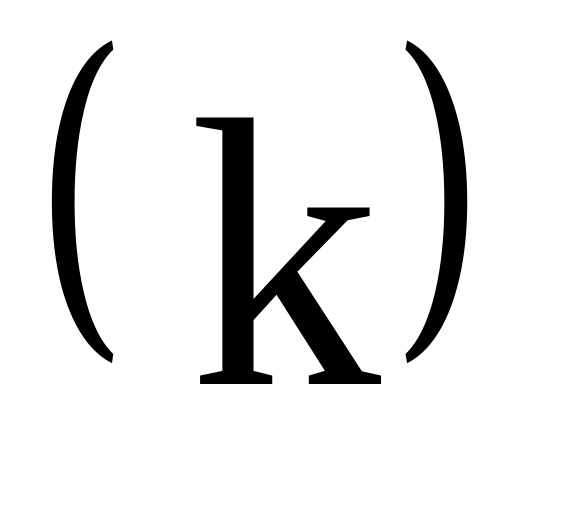 .
.
Розв’язування 1.2
При гармонічних коливаннях рівняння коливань у загальному випадку записується так:
22
![]() (1)
(1)
де ![]() – амплітуда
коливання;
– амплітуда
коливання;
![]() –
фаза коливання;
–
фаза коливання;
– початкова фаза коливання;
– циклічна частота;
![]() – час
від початкового моменту.
– час
від початкового моменту.
Тоді згідно умови розв’язком задачі є:
Амплітуда коливання =0,1 м.
Колова частота
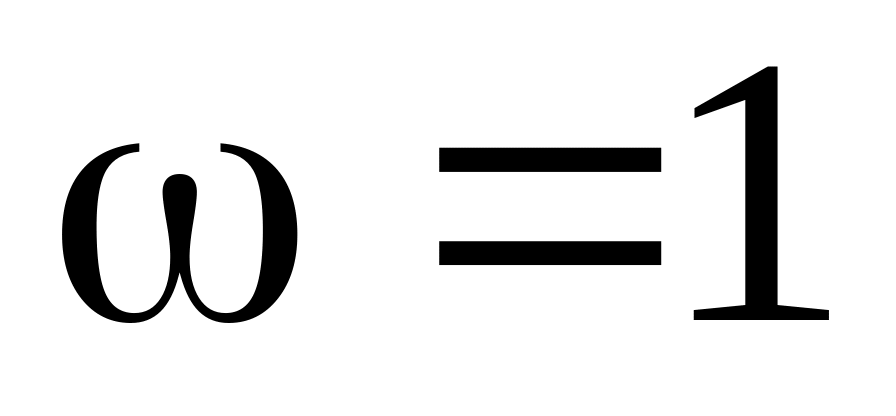 .
.Частоту
 визначаємо з рівняння
визначаємо з рівняння
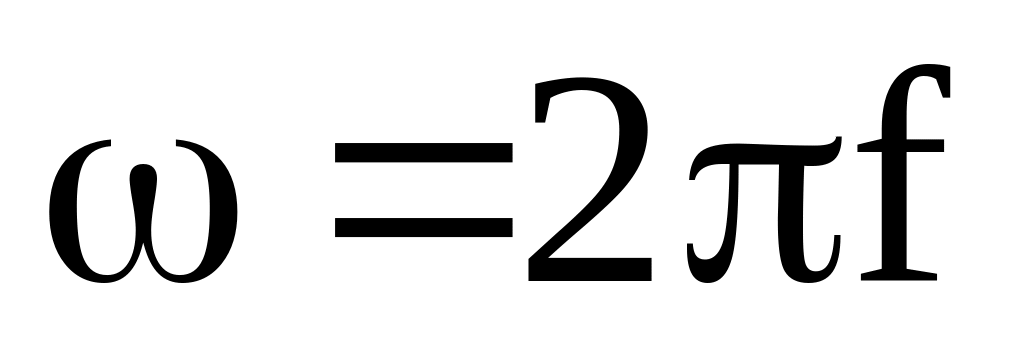 .
Звідси
.
Звідси
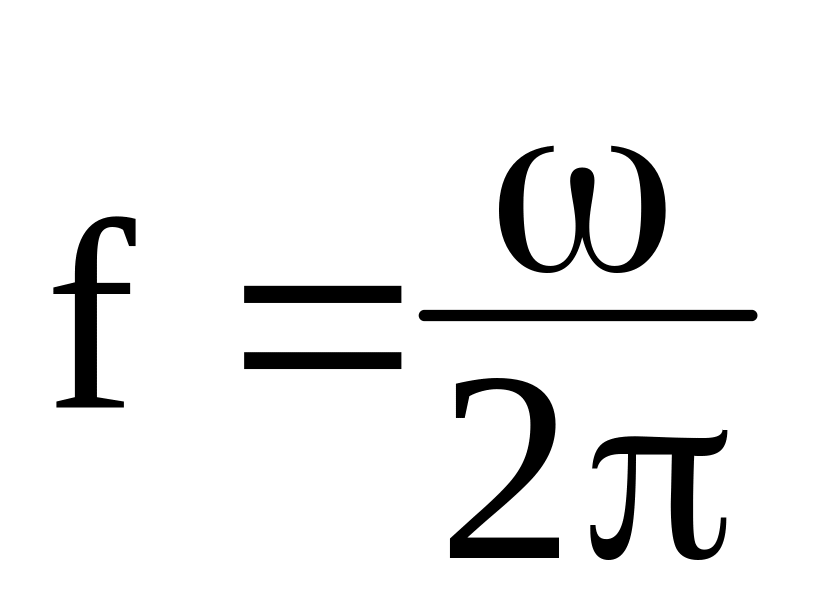 [Гц].
[Гц].Період
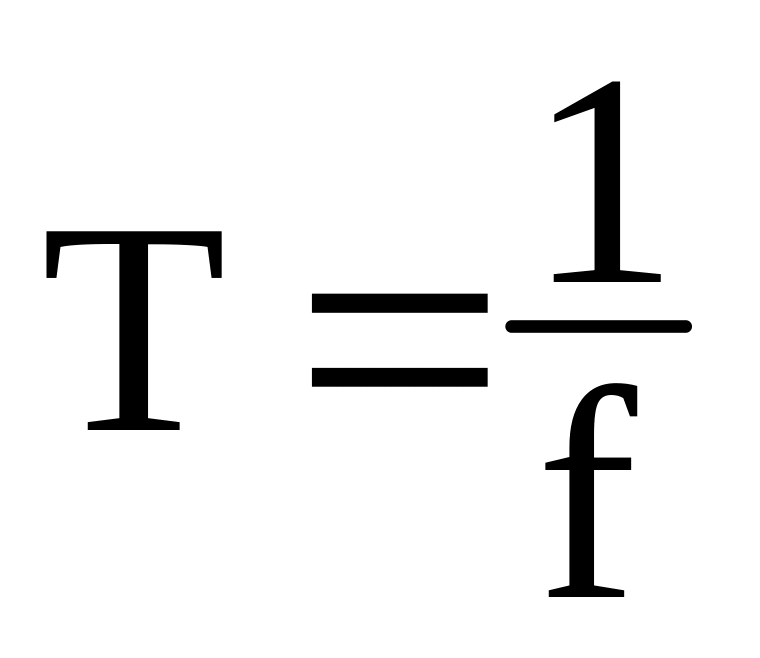 .
Тоді, знаючи
з п.3
.
Тоді, знаючи
з п.3
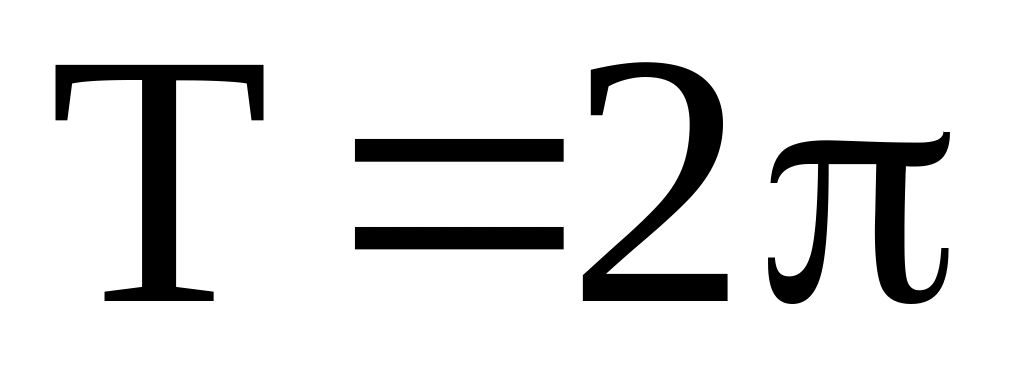 [c].
[c].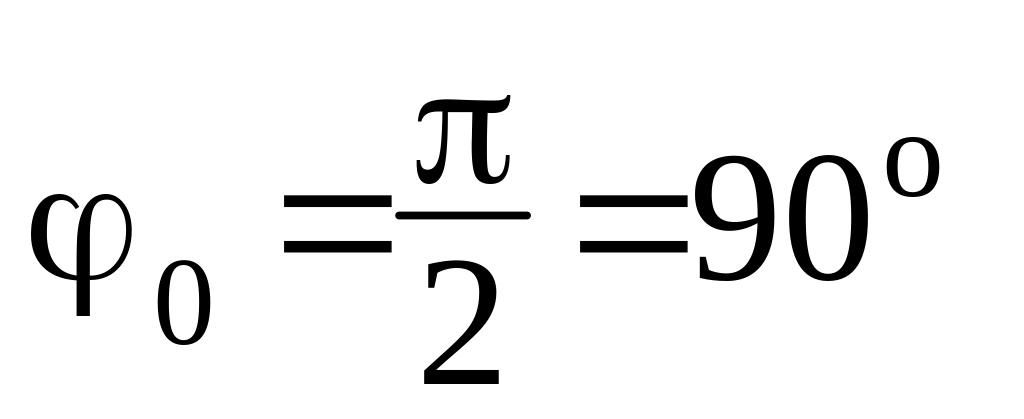 .
.Повна енергія складається із потенціальної
 і кінетичної
і кінетичної
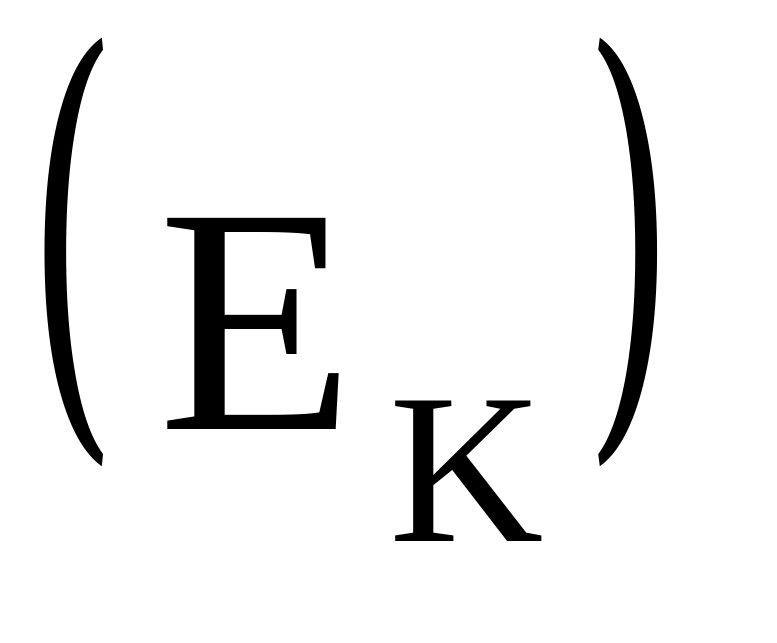 .
В процесі коливання проходить перетворення
кінетичної енергії в потенціальну і
зворотній процес. Причому в момент
найбільшого відхилення від положення
рівноваги повна енергія
складається тільки із потенціальної
енергії, яка досягає свого максимального
значення
.
В процесі коливання проходить перетворення
кінетичної енергії в потенціальну і
зворотній процес. Причому в момент
найбільшого відхилення від положення
рівноваги повна енергія
складається тільки із потенціальної
енергії, яка досягає свого максимального
значення
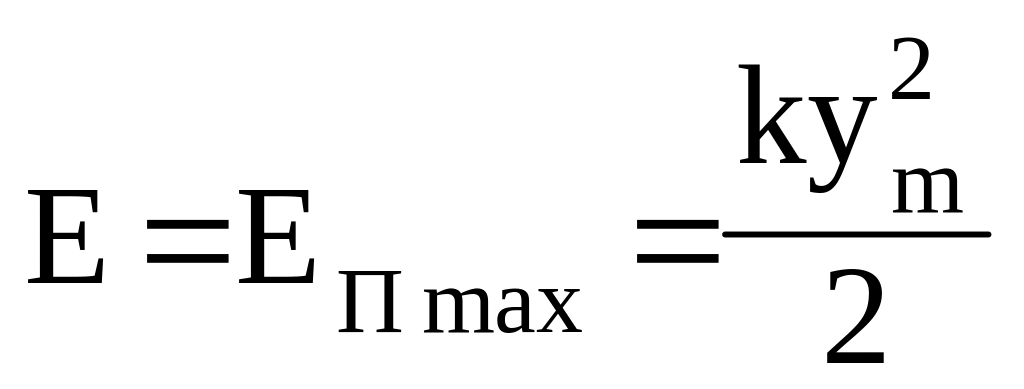 .
А при проходженні системи через положення
рівноваги повна енергія
складається лише з кінетичної енергії,
яка в цей момент досягає найбільшого
значення
.
А при проходженні системи через положення
рівноваги повна енергія
складається лише з кінетичної енергії,
яка в цей момент досягає найбільшого
значення
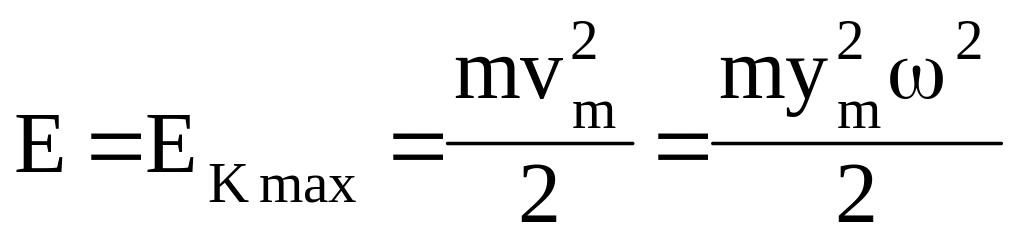 .
.
Значить повна енергія
![]() для нашого випадку слідуюча:
для нашого випадку слідуюча:
![]()
23
Максимальна швидкість руху вантажу
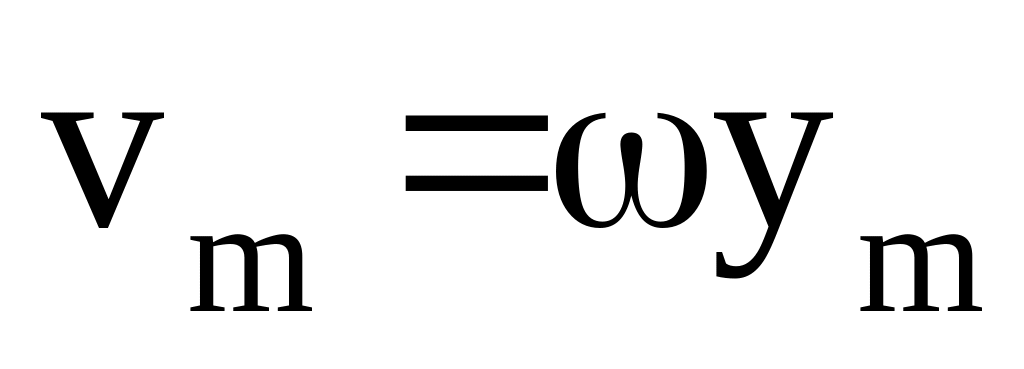 :
:
![]() .
.
Коефіцієнт жорсткості пружини знаходимо з порівняння максимальних значень кінетичної і потенціальної енергій:
![]() ;
; ![]() ;
;
![]() .
.
Задача 1.3
Осцилограма затухаючих коливань має
![]() коливань. Амплітуда першого коливання
коливань. Амплітуда першого коливання
![]() мм і наступного
мм і наступного
![]() мм. Вважаючи, що час протягом якого
відбуваються ці коливання дорівнює
мм. Вважаючи, що час протягом якого
відбуваються ці коливання дорівнює
![]() ,
визначити:
,
визначити:
Період , частоту і колову частоту коливань.
Логарифмічний декремент затухання коливань .
Коефіцієнт затухання коливань .
Сталу часу
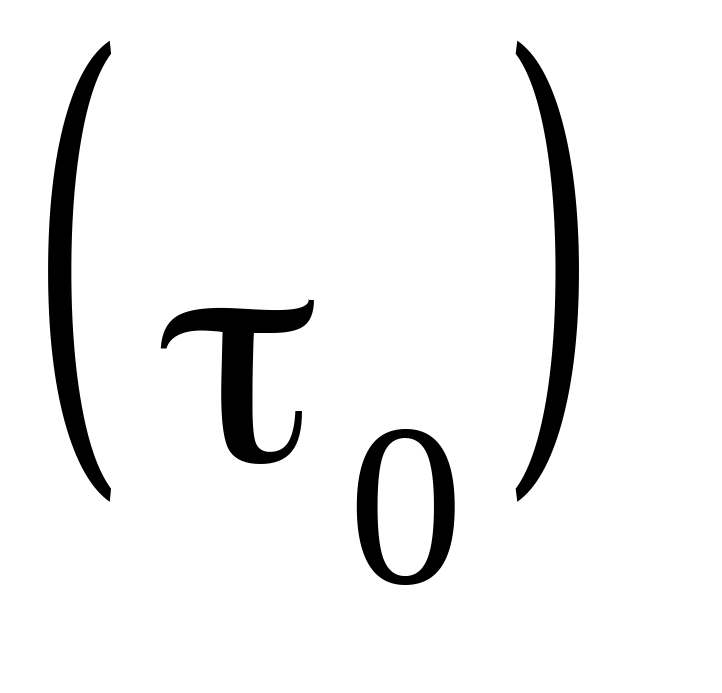 .
.Коефіцієнт опору системи
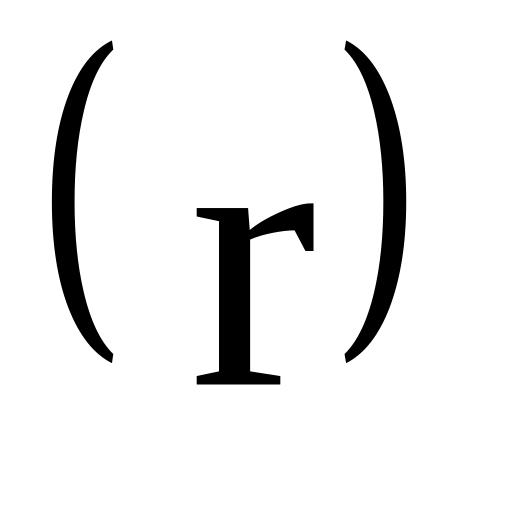 .
.Хвильовий (характеристичний) опір системи
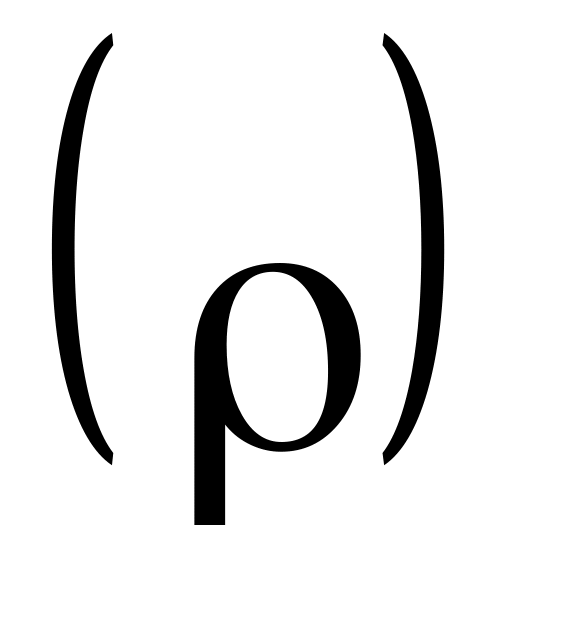 .
.Добротність системи
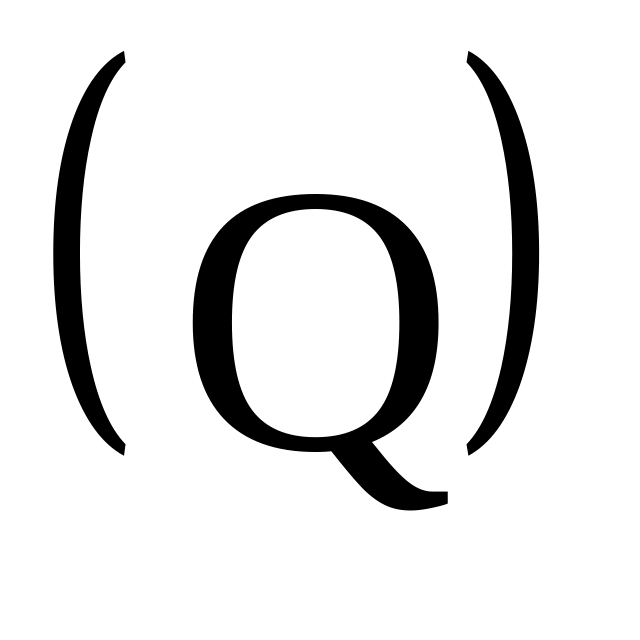 .
.
Розв’язування 1.3
Період коливання визначаємо за формулою
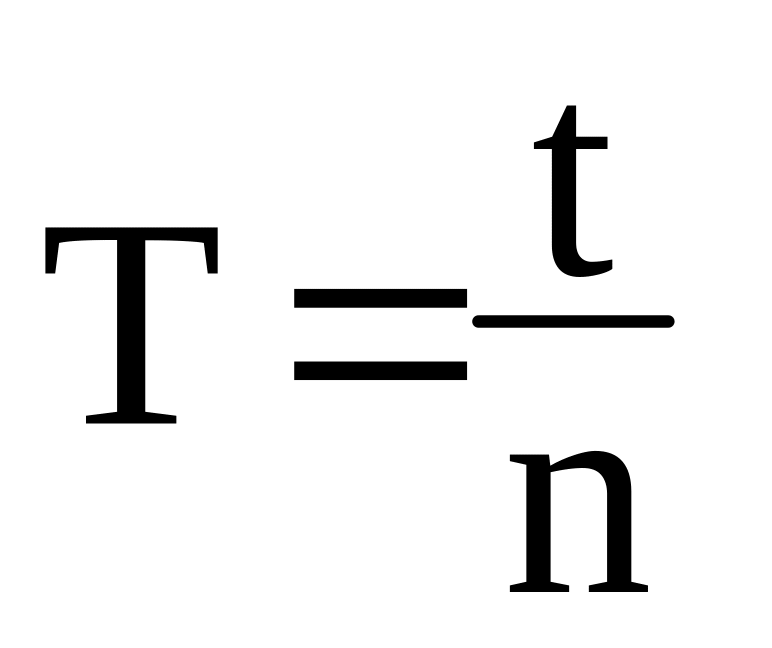 ,
де
–
час коливання;
,
де
–
час коливання;
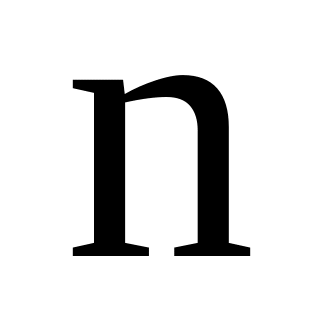 –
кількість коливань, які відбулися
протягом цього часу. У нашому випадку
–
кількість коливань, які відбулися
протягом цього часу. У нашому випадку
 ,
а
.
Отже,
,
а
.
Отже,
 .
.
24
Частота
![]() ;
;
![]() .
.
Колова частота
![]() ;
;
![]() .
.
Логарифмічний декремент затухання
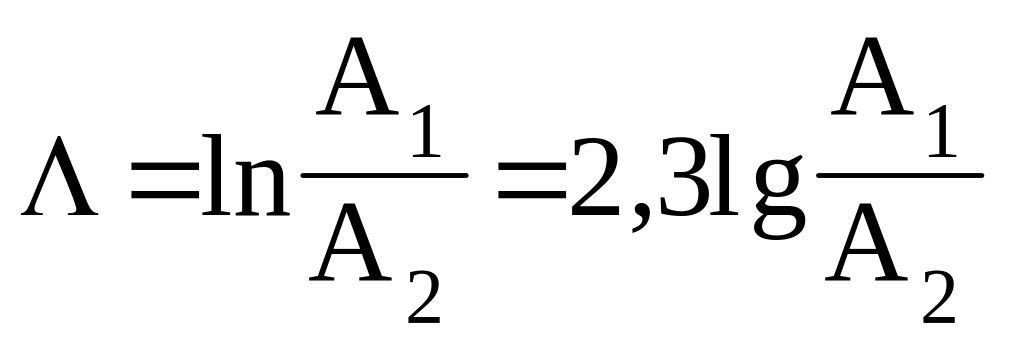 ,
де
,
де
 і
і
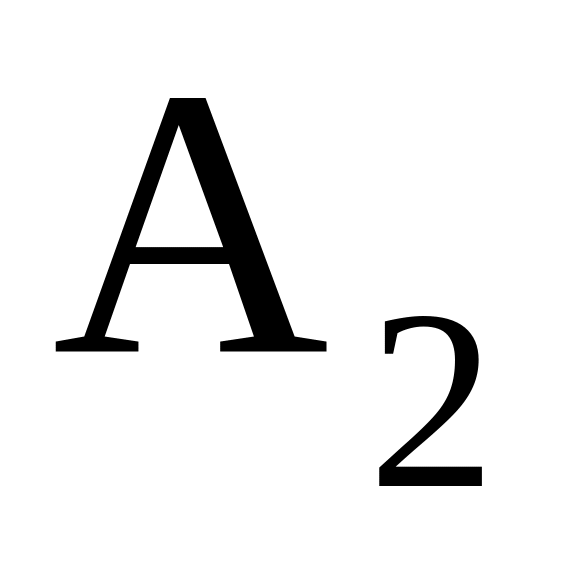 – амплітуди коливань, віддалені одна
від одної на період.
Знаючи
і
визначаємо
– амплітуди коливань, віддалені одна
від одної на період.
Знаючи
і
визначаємо
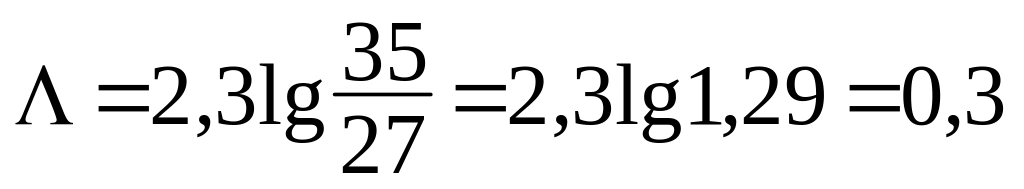 .
.Враховуючи, що амплітуда
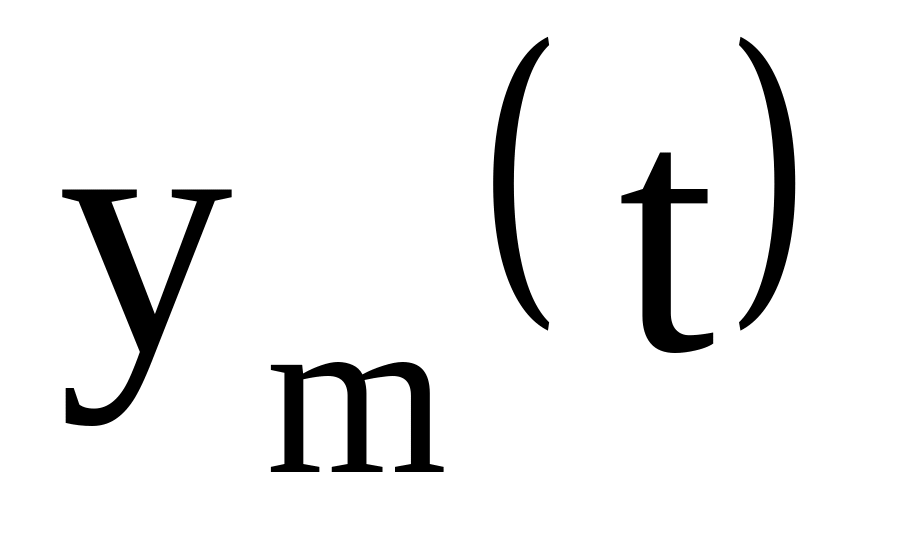 затухаючих коливань змінюється за
формулою:
затухаючих коливань змінюється за
формулою:
![]() ,
,
знайдемо значення амплітуд, які
відповідають моментам часу, що
відрізняються на період (згідно визначення
![]() )
)
 .
.
Одержаний вираз називають декрементом затухання, а його логарифм – логарифмічним декрементом затухання:
![]() .
.
З приведеного рівняння знаходимо
коефіцієнт затухання коливань
![]() :
:
![]() .
.
Стала часу
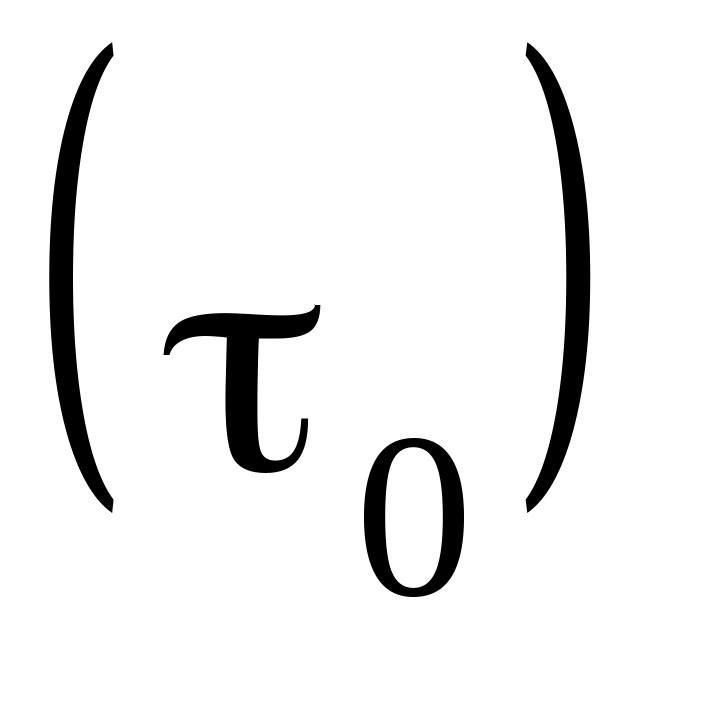 – це є інтервал часу, протягом якого
амплітуда коливань зменшується в
– це є інтервал часу, протягом якого
амплітуда коливань зменшується в
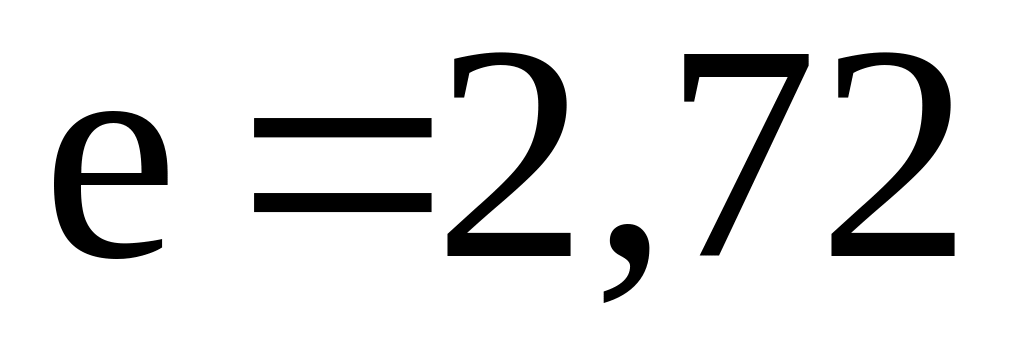 раз. Цю сталу часу визначають через
коефіцієнт затухання
раз. Цю сталу часу визначають через
коефіцієнт затухання
 ;
;
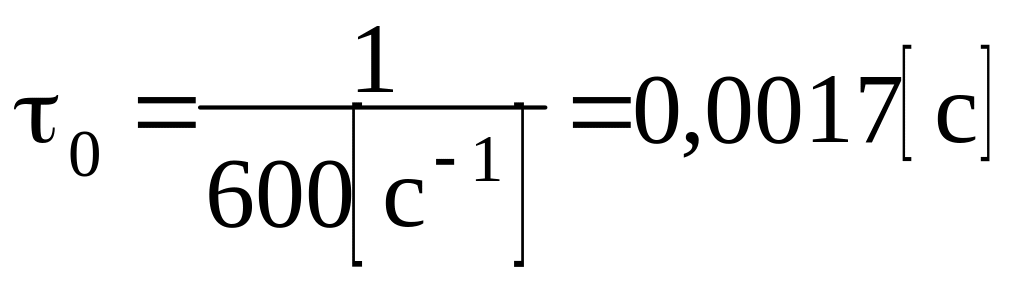 .
.
25
Коефіцієнт опору системи визначається через коефіцієнт затухання і масу вантажу, що коливається. Для коливань вантажу на пружині
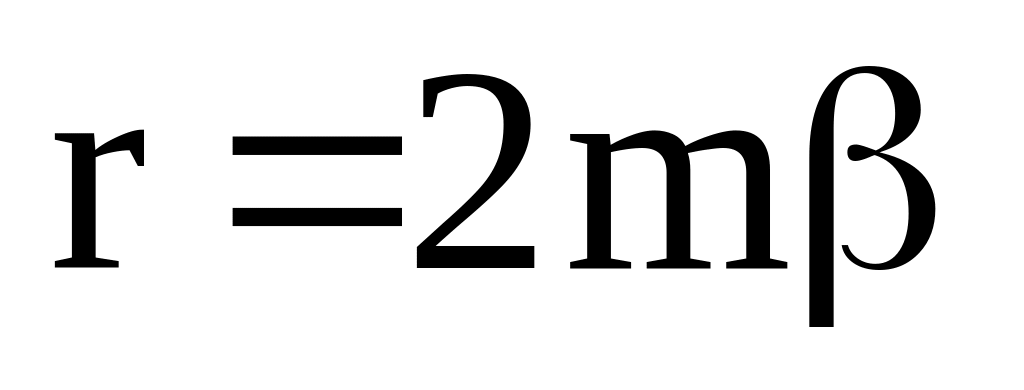 .
.Хвильовий (характеристичний) опір системи для коливань вантажу на пружині визначають за формулою:
 .
.Добротність системи визначається відношенням характеристичного опору до коефіцієнта опору , тобто
![]() .
.
Задача 1.4
Яка частота, амплітуда і початкова фаза
коливання, яке задається рівнянням
![]() ?
?
Розв’язування 1.4
Частоту коливання знаходимо за формулою
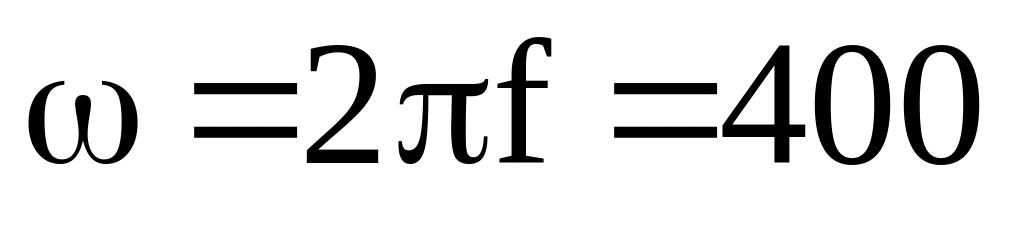 ;
;
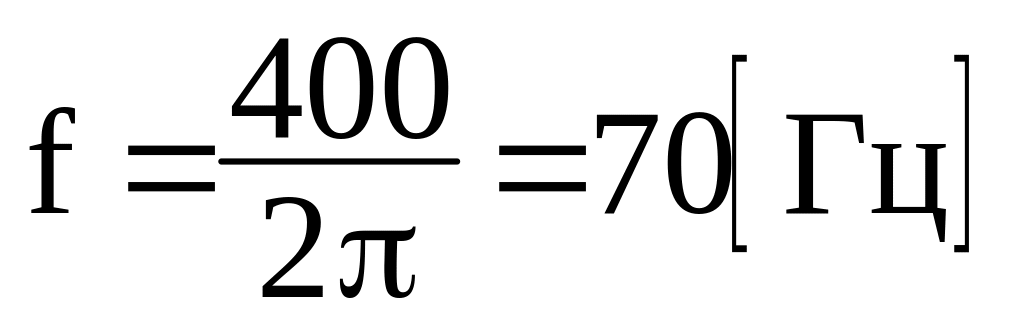 .
.Амплітуда коливання
 м.
м.Початкова фаза коливання
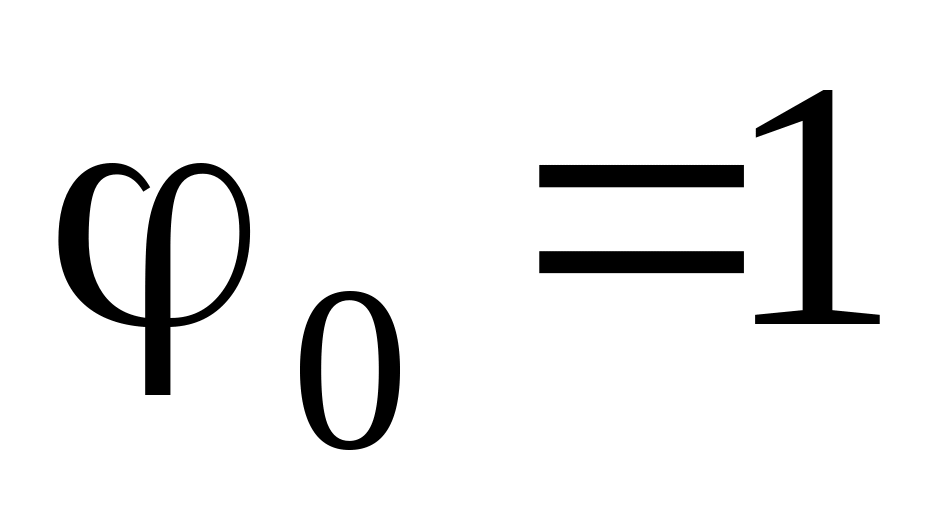 рад
рад
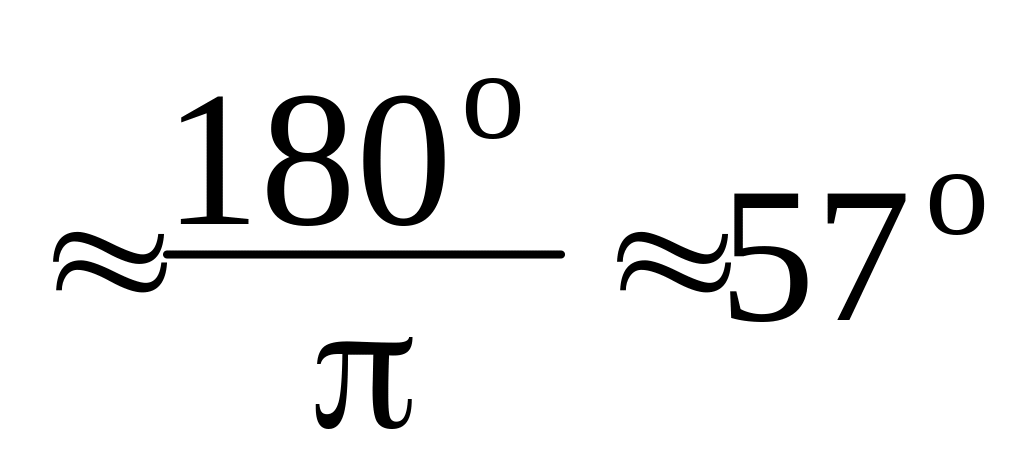 .
.
Задача 1.5
Написати рівняння гармонічного
коливального руху з амплітудою в 5 см,
якщо за одну хвилину виконується 150
коливань і початкова фаза коливань
дорівнює
![]() .
.
Розв’язування 1.5
Загальне рівняння гармонічного
коливального руху має вигляд:
![]() .
.
Знаходимо, що
![]() м.
м.
26
Відомо, що
![]() ,
де
,
де
![]() ;
тоді
;
тоді
![]() .
.
Таким чином, рівняння буде мати вигляд:
![]() .
.
Задача 1.6
Маємо вантаж на пружині (мал. ). Визначити:
Жорсткість пружини.
Роботу, виконану силою тяжіння під час розтягування пружини.
Максимальну швидкість, якої набуде тіло, що здійснює коливання, якщо зникне сила тяжіння.
Колову частоту, частоту і період коливань даного вантажу на пружині (один з варіантів цього завдання можна перевірити експериментально, зібравши демонстраційну установку).
Довжину нитяного (математичного) маятника, який матиме такий період коливань, як і даний вантаж на пружині (результат можна запропонувати перевірити експериментально).
Розв’язування 1.6
1. За законом Гука, сила пружності пропорційна деформації тіла:
![]() ,
,
де
![]() – жорсткість пружини (коефіцієнт
пропорційності між силою пружності і
деформацією тіла).
– жорсткість пружини (коефіцієнт
пропорційності між силою пружності і
деформацією тіла).
Звідси
27
![]() ,
,
де сила пружності
![]() дорівнює силі земного тяжіння, що діє
на вантаж:
дорівнює силі земного тяжіння, що діє
на вантаж:
![]()
а деформація
![]()
(її можна знайти за початковим і кінцевим положенням стрілки відносно лінійки).
Отже
![]()
![]()
2. Роботу, виконану силою земного тяжіння
при розтягуванні пружини, можна визначити
за різницею потенціальних енергій
пружини в кінцевому
![]() і початковому
і початковому
![]() станах:
станах:
![]()
Потенціальна енергія в початковому стані (пружина не розтягнута) дорівнює нулю. Отже
![]() ;
; ![]()
![]()
![]()
3. Потенціальну енергію пружно деформованої
пружини визначаємо за формулою
![]() .
За законом збереження механічної енергії
(при нехтуванні її втратами), максимальне
значення механічної енергії
.
За законом збереження механічної енергії
(при нехтуванні її втратами), максимальне
значення механічної енергії
28
![]() .
.
Прирівнявши максимальне значення потенціальної енергії до максимального значення кінетичної енергії, можна знайти максимальне значення швидкості, яку матиме тіло при коливаннях, якщо раптом зникло б земне тяжіння:
![]()
![]()
Але
![]()
Тому
![]()
![]()
![]()
Колову частоту коливань на пружині можна визначити за формулою
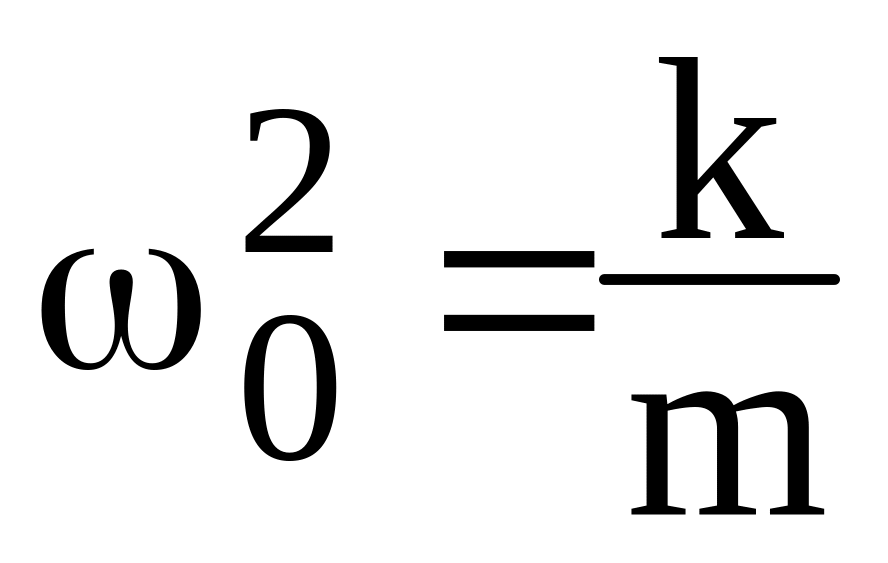 .
.
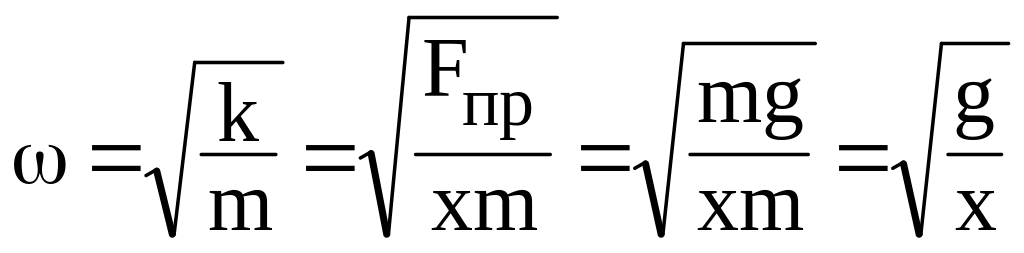 ;
;
![]() .
.
Оскільки колова частота пов’язана із
звичайною частотою співвідношенням
![]() ,
то
,
то
![]() ;
;![]() .
.
Період коливань
![]() ;
;
![]()
29
Період коливань вантажу на пружині визначають за формулою
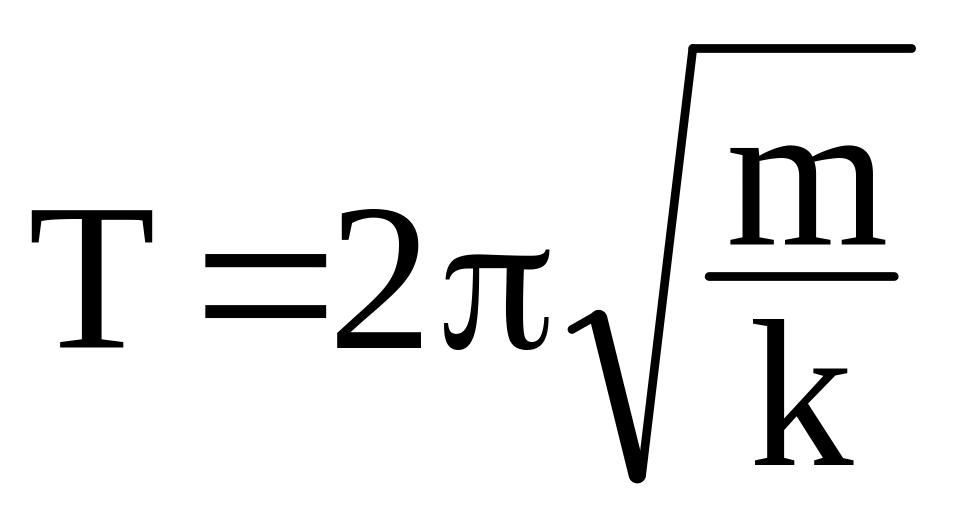 .
За розтягом пружини
під дією вантажу можна знайти жорсткість
пружини:
.
За розтягом пружини
під дією вантажу можна знайти жорсткість
пружини:
 .
Отже,
.
Отже,
 .
Формула для визначення періоду коливань
нитяного маятника:
.
Формула для визначення періоду коливань
нитяного маятника:
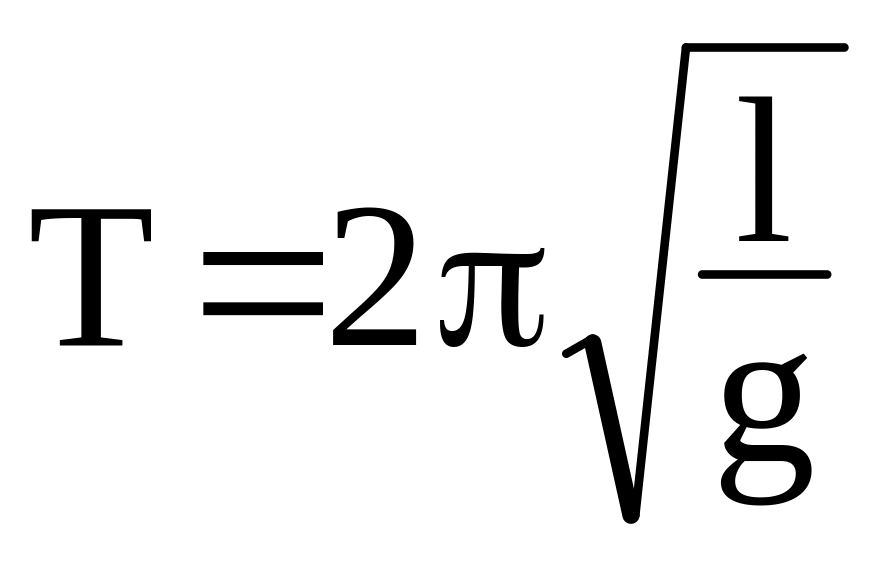 .
Оскільки періоди коливань обох маятників
повинні бути однаковими, то
.
Оскільки періоди коливань обох маятників
повинні бути однаковими, то
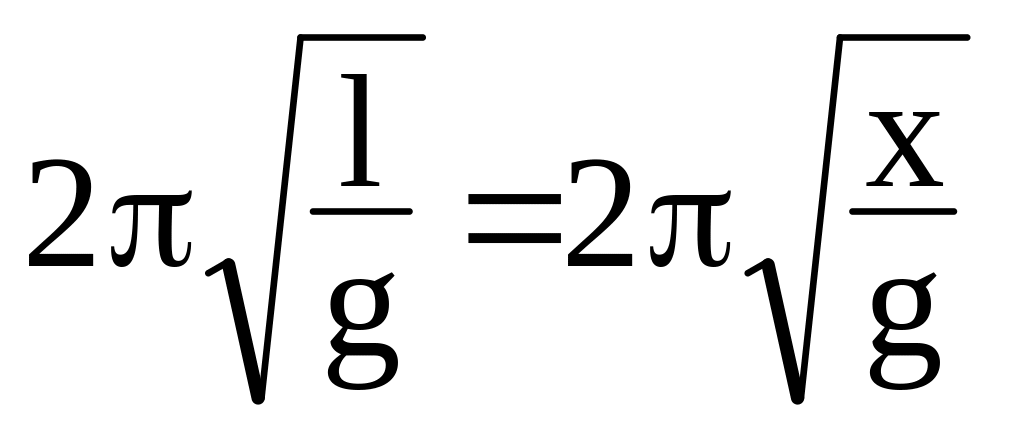 ;
;
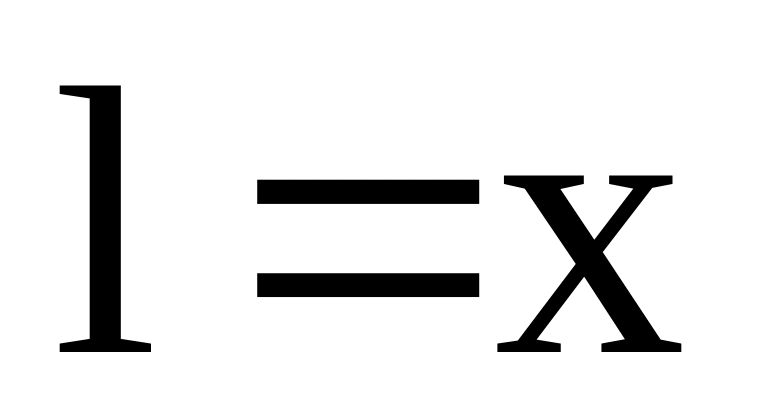 .
У нашому випадку
.
У нашому випадку
 .
Тепер виготовляємо нитяний маятник
такої довжини, визначаємо експериментально
період його коливань і впевнюємося у
тому, що цей період дорівнює періоду
коливань даного тягаря на пружині.
.
Тепер виготовляємо нитяний маятник
такої довжини, визначаємо експериментально
період його коливань і впевнюємося у
тому, що цей період дорівнює періоду
коливань даного тягаря на пружині.
30
