33.Вычитающие счетчик

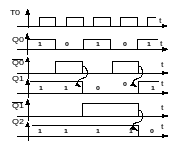
Вычитающий счётчик с последовательным переносом имеет обратный порядок смены состояний: с приходом очередного счётного импульса содержащееся в счётчике число умень­шается на единицу (табл.5.2).

Процесс двоичного счета вычитающегоо счетчика

Номер состояния	Q2	Q1	Q0	Т0
0	1 1	1 1	1 0	0 1
1	1 1	1 0	0 1	0 1
2	1 1	0 0	1 0	0 1
3	1 0	0 1	0 1	0 1
4	0 0	1 1	1 0	0 1
5	0 0	1 0	0 1	0 1
6	0 0	0 0	1 0	0 1
7	0 1	0 1	0 1	0 1

Другая особенность вычитающего счётчика - триггер каждого последующего разряда переключается в противоположное состояние при изменении уровня на выходе триггера предыдущего разряда от 0 к 1, т.е. при сигнале займа, обратном сигналу пере­носа в суммирующем счётчике.

Строится вычитающий счётчик так же, как суммирующий, но с тем отличием, что со входом каждого последующего триггера в отличие от Рис.5.2.а соединяется инверсный выход предыдущего триггера.

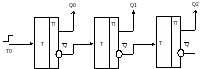
Кроме суммирующих и вычитающих счетчиков имеются реверсивные счетчики.

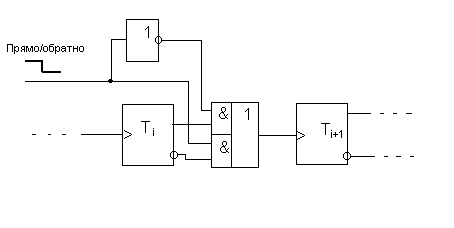
Реверсивные счетчики изменяют направление счета под воздействием управляющего сигнала. На Рис. 5.2 и 5.3 видно, что счетчики прямого и обратного счета различаются лишь точкой съема сигнала, подаваемого с предыдущего разряда на последующий. Если управляющий сигнал перестраивает межразрядные связи, перенося точку съема сигнала с одного выхода триггера на другой, то реализуется схема реверсивного счетчика (Рис.5.4).

Рис. 5.4. Реверсивный счетчик

У асинхронных счетчиков (или счетчиками с последовательным переносом) каждый триггер переключается выходным сигналом предыдущего триггера. Временные состязания сигналов в таких счетчиках отсутствуют, поскольку триггеры переключаются поочередно, один за другим. Последовательные счетчики отличаются простотой схемы, но обладают низким быстродействием.

34. Сумматор

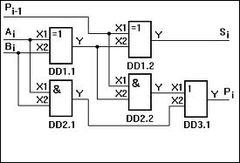
Cхема, которая обеспечивает сложение двух однобитных чисел А и В называется полусумматором. Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса (P). При этом S наименее значимый бит, а P наиболее значимый бит.

Объединив два полусумматора и добавив дополнительную схему ИЛИ, можно создать полный сумматор с дополнительным входом P_i-1 (на рисунке 1), который принимает сигнал переноса из предыдущей схемы.

Схема полного сумматора может быть использована в качестве "строительных блоков" для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.

Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом. Все три операнда и оба выходных разряда однобитные.

Может быть построен как тринарная (трёхоперандная) двоичная функция с бинарным выходом, но, для уменьшения аппаратных затрат, обычно строится трёхступенчатым, состоящим из трёх узлов: двух полусумматоров, которые являются полными бинарными (двухоперандными) двоичными логическими функциями с унарным выходом и логического элемента «2ИЛИ».