1.RC-фильтры
Фильтры высоких частот.
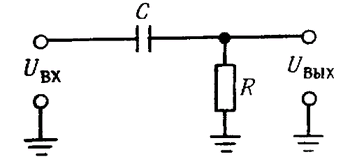
Фильтры высоких частот. Согласно закону Ома для комплексных величин,
I = Uвх/Zполн = Uвх/R - (j/ωC) = Uвх[R + j/ωC)]/R2 + 1/ω2C2.
Uвых = IZR = IR = Uвх[R + (j/ωС)R]/R2+1/ω2C2.
Чаще всего нас интересует не фаза, а амплитуда Uвых:
Uвых = (UвыхUвых*)1/2 = UвхR/[R2 + (1/ω2C2)]1/2.
Итак, если не принимать во внимание сдвиг фаз, а рассматривать только модули комплексных амплитуд, то «отклик» схемы будет определяться следующим образом:
Uвых = UвхR/[R2 + (1/ω2C2)]1/2 = Uвх2πƒRC/[1 + (2πƒRC)]1/2.
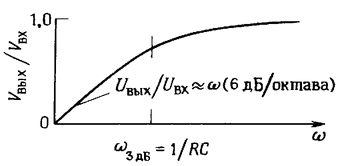
Фильтры низких частот. Если поменять местами R и С (рис. 1.58), то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC.
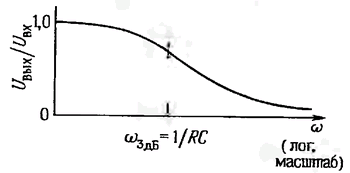
Полосовой фильтр
П
олосовой
фильтр получается соединением фильтров
верхних и нижних частот, он пропускает
частоты в определенном диапазоне
3.Дифференцирующие и интегрирующие цепи
Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).
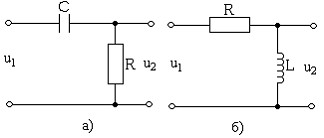
Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.
Тогда для этой цепи справедливо соотношение
и с учетом преобразований будем иметь
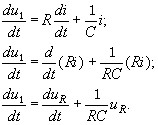(3.114)
Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.
При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда
(3.115)
т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.
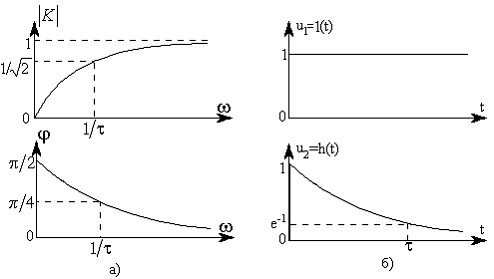
Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.
Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если
,
или медленными, если
.
Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.
Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:
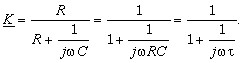(3.116)
При малых τ, а именно когда τ<<1/ω, выражение (3.116) преобразуется в
.
При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.
В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):
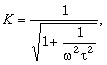(3.118)
а аргумент K, или фазовая характеристика этой цепи:
(3.119)
Эти зависимости показаны на рис. 3.21,а.
Если
в качестве выходного сигнала взять
единичный скачок напряжения 
,
то интегрированием уравнения (3.114) можно
получить переходную характеристику
дифференцирующей цепи, или временную
зависимость выходного сигнала при
единичном скачке напряжения на входе:
(3.120)
График переходной характеристики показан на рис. 3.21,б.
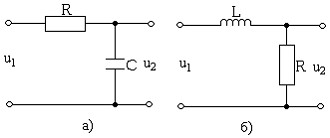
Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.
Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением
или
(3.121)
При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:
(3.122)
Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.
Коэффициент передачи интегрирующей цепи определяется выражением
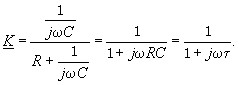(3.123)
При ω<<1/τ K≈1.
Частотная и фазовая характеристики описываются соответственно выражениями
(3.124)
(3.125)
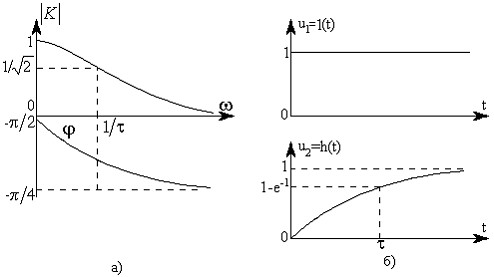
Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.
и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при :
(3.126)
При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.