Раздел 1 применение методов интегрирования функции в задачах лазерных технологий Теоретические сведения

1. Неопределенный интеграл

Первообразной функцией от функции , определенной на некотором отрезке , называется функция , определенная на том же отрезке и удовлетворяющая условию:

.

Если функция имеет первообразную, то она имеет бесчисленное множество первообразных, которые отличаются друг от друга на постоянное слагаемое С.

Неопределенным интегралом функции называют общее выражение , где С – произвольная постоянная:

.

Для нахождения неопределенного интеграла функции пользуются таблицей интегралов.

2. Определенный интеграл

Пусть функция определена на отрезке . Разобьем отрезок на n элементарных отрезков и в каждом из них выберем точку .

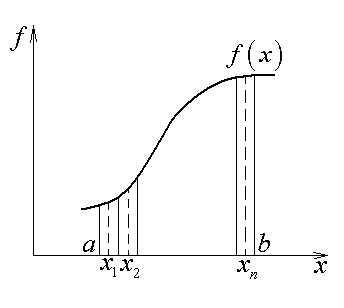
Рис. 1.1. К определению определенного интеграла.

Определенным интегралом функции на отрезке называется предел суммы произведений длин отрезков на значение функции в выбранной на отрезке точке, при условии, что количество отрезков n стремится к бесконечности, а длина каждого отрезка стремится к нулю ( ):

,

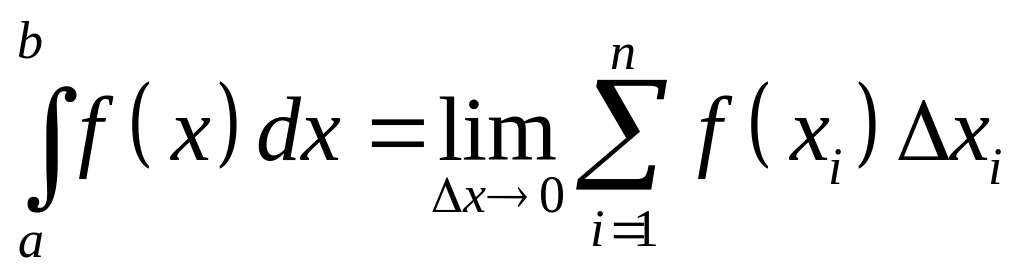где величина а называется нижним пределом интегрирования, а b – верхним пределом. Нетрудно видеть, что геометрически определенный интеграл выражает площадь под графиком функции.

По определению принимается:

,

.

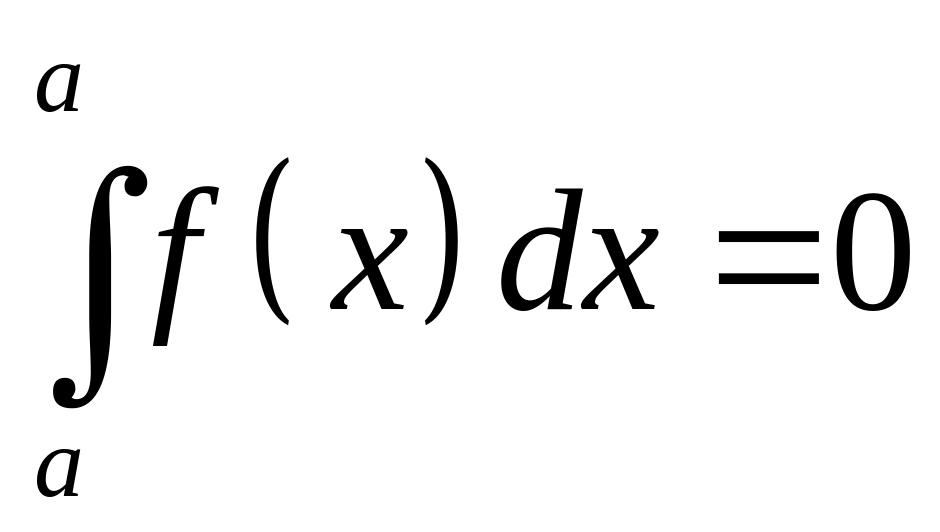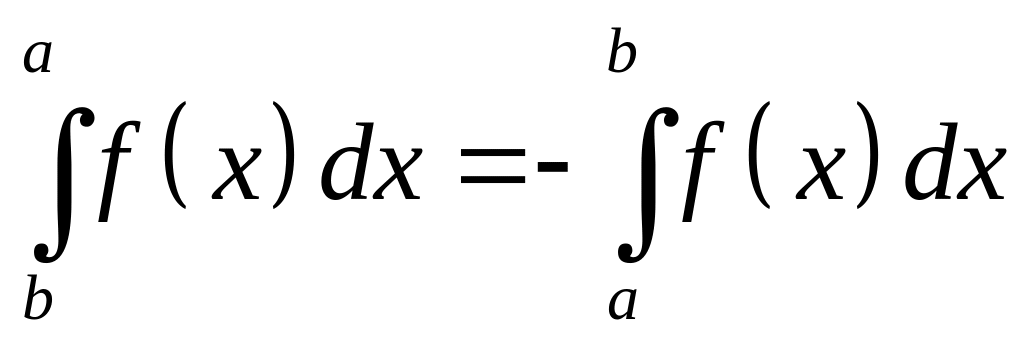Определенный интеграл может быть выражен через неопределенный с помощью формулы Ньютона-Лейбница:

.

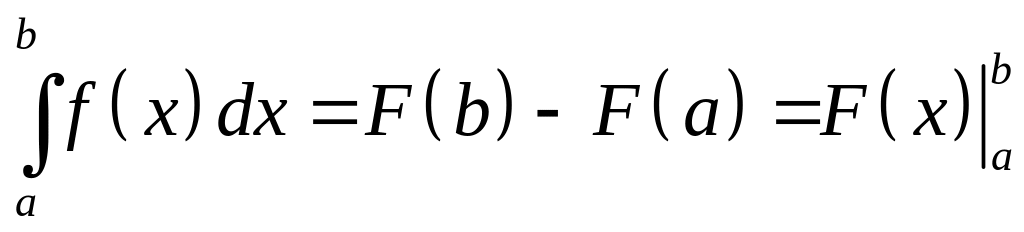Это позволяет вычислять определенные интегралы с помощью таблиц неопределенных интегралов.

Другие свойства определенных интегралов:

,

,

,

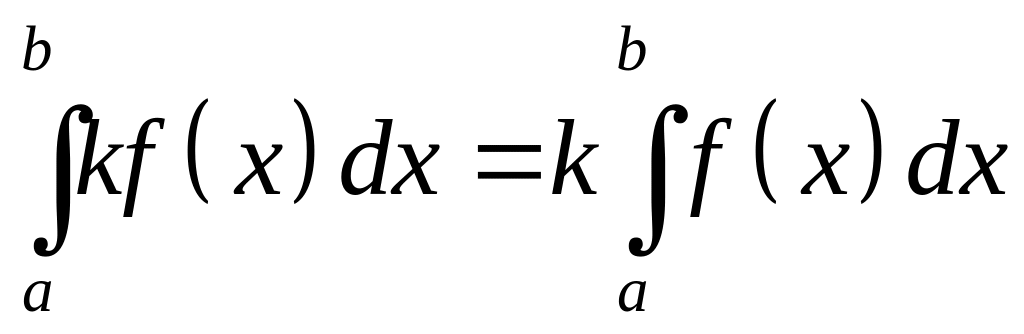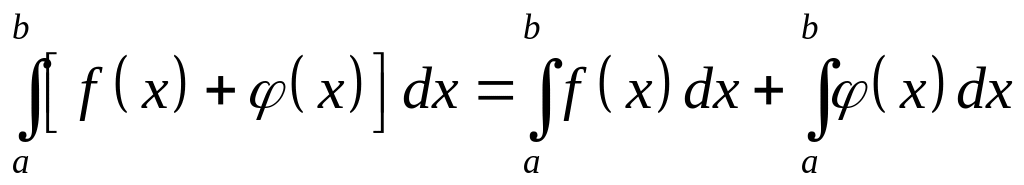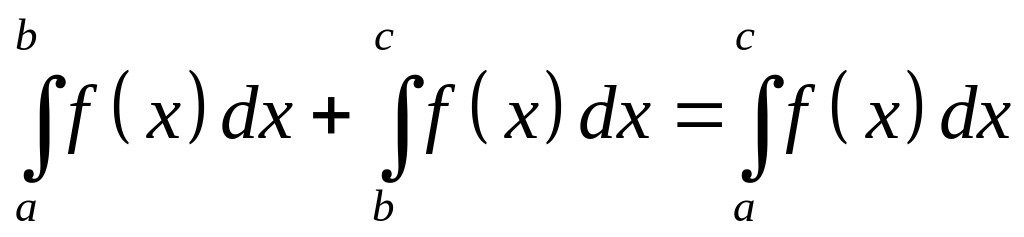, (1.10)

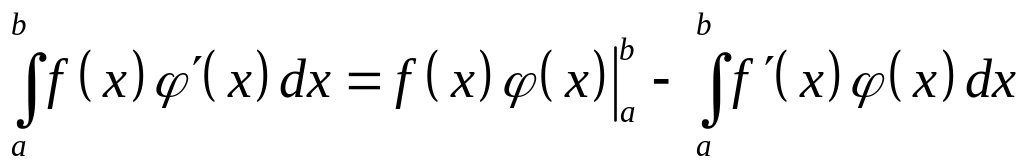. (1.11)

Эти свойства, а также таблица неопределенных интегралов позволяют нам производить вычисления интегралов.

3. Несобственные интегралы

Если в интеграле в качестве одного или обоих пределов интегрирования стоит бесконечность ( или ), то такой интеграл относится к так называемым несобственным интегралам. За исключением отдельных нюансов действия с ними производятся так же, как и с обычными определенными интегралами.

4. Интегрирование функций нескольких переменных

Ограничимся рассмотрением двух переменных. Пусть в области G задана функция . Двойной интеграл определяется как предел суммы произведений площадей элементарных площадок на значения функции в произвольных точках, выбранных на этих площадках:

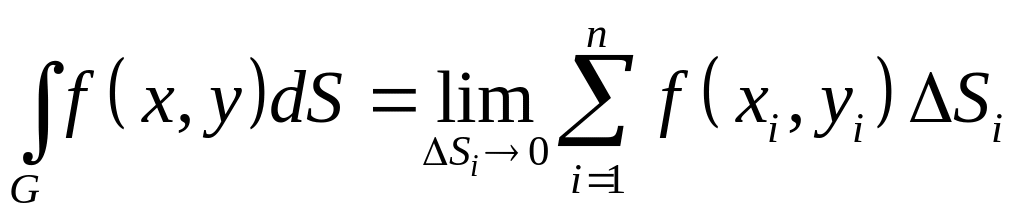. (1.12)

Рис. 1.2. К определению двойного интеграла.

Вычисляется двойной интеграл как двукратный, последовательным интегрированием по каждой координате:

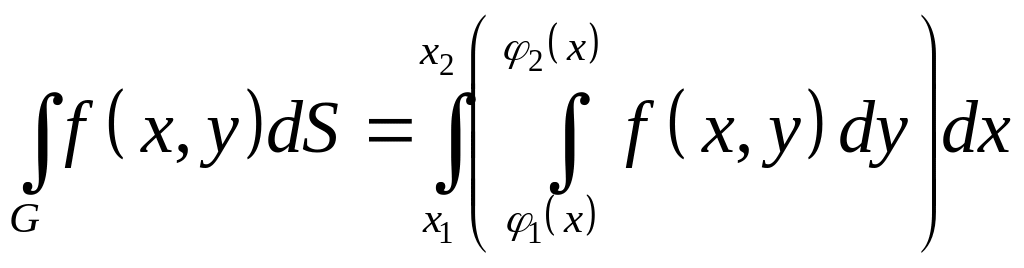. (1.13)

Рис.1.3. Вычисление двойного интеграла.

Если область сложная, ее разбивают на несколько простых областей, в каждой из которых вычисляется интеграл, а результаты складываются.