11

Л-02.

Динаміка матеріальної точки та поступального руху твердого тіла

Динаміка – розділ механіки в якому вивчення руху тіл відбувається в зв’язку з діючими на них силами. Іншими словами в цьому розділі вивчаються причини руху тіл.

2.1 Закони Ньютона. Маса. Сила. Інерціальні системи відліку

1-й закон Ньютона ( закон інерції). Всяке тіло зберігає стан спокою, або рівномірного прямолінійного руху до тих пір, поки дія інших тіл не виведе його із цього стану.

v = const при F = 0. (2.1)

Властивість тіл зберігати набутий стан (спокою, чи руху) називається інертністю.

Мірою інертності тіл є маса (m), яка в СІ вимірюється в кг.

Системи відліку, в яких тіла, що не зазнають дії інших тіл, знаходяться у стані відносного спокою, або рівномірного прямолінійного руху, називаються інерціальними. Всі системи відліку, які рухаються відносно інерціальної рівномірно і прямолінійно, або знаходяться у стані спокою, теж являються інерціальними. Всі інші системи неінерціальні. Закони Ньютона справедливі для інерціальних систем.

Сила (F) – це міра дії одного тіла на інше, яка проявляється у виникненні прискорення тіла, або в його деформації (зміні розмірів і форми).

2-й закон Ньютона. Прискорення, з яким рухається тіло, прямо пропорційне векторній сумі сил, що діють на нього, обернено пропорційне масі тіла і направлене в сторону дії рівнодіючої сили.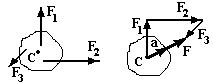

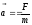. (2.2)

З цього закону визначається одиниця сили, яку в системі СI називають ньютоном:

.

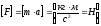3-й закон Ньютона. Два тіла взаємодіють з силами F₁ і F₂, однаковими за величиною, протилежними за напрямом і мають одну і ту ж природу.

. (2.3)

Ці сили не зрівноважують одна одну, так як прикладені до різних тіл.

2.2 Імпульс тіла. Загальне формулювання 2-го закону Ньютона. Закон збереження імпульсу

Враховуючи, що прискорення 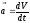, формула (2.2) 2-го закону Ньютона буде мати вигляд:

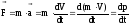. (2.4)

Тут добуток маси тіла на швидкість його руху називається імпульсом 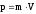. Це векторна фізична величина. Швидкість його зміни з часом дає силу. Змінити ж імпульс тіла можна не тільки за рахунок зміни швидкості, а і за рахунок зміни його маси. Тому формула (2.4) 2-го закону Ньютона є більш загальною. Таке формулювання дає можливість вивчати рух тіл змінної маси, наприклад, рух ракети.

Одиницею величини імпульсу тіла є

.

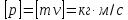2.4 Сили в механіці. Сила пружності. Закон Гука

Деформацією називається зміна форми, або об’єму тіла під дією зовнішніх сил (в певних умовах тіло можуть деформувати і внутрішні сили). Розрізняють два ідеальних види деформацій: абсолютно пружні і абсолютно пластичні деформації. При абсолютно пружній деформації форма і розміри тіла повністю відтворюються після припинення дії зовнішньої сили. При абсолютно пластичній, навпаки, форма і розмір тіла після припинення дії сили повністю зберігають набутий при деформації стан.

Сили, які виникають при пружних деформаціях, називаються пружними силами. Існують деформації : розтягування (стискання); згинання; кручення; зсуву. Різні види деформацій можна звести до двох основних: розтягування (стискання) і зсуву.

Розглянемо, як приклад, деформацію розтягування (стискання). Англійський фізик Р.Гук у 1660 році експериментально встановив закон, який носить його ім’я: при малих пружних деформаціях сила пружності пропорційна величині деформації

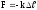, (2.5)

k – коефіцієнт жорсткості, - величина деформації. Знак (-) мінус вказує, що сила пружності направлена в сторону, протилежну деформації, тобто має такий напрямок, щоб зменшити деформацію.

Нехай стержень довжиною ℓ площею перерізу S і поперечним розміром d закріплений за один кінець, а до другого прикладена розтягуюча зовнішня сила . Внаслідок цього довжина стержня збільшується на величину ∆ℓ, а поперечний розмір зменшується на ∆d. Виникає пружна сила . Експерименти показують, що абсолютне видовження ∆ℓ прямо пропорційне силі 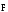, довжині стержня ℓ і обернено пропорційне площі перерізу S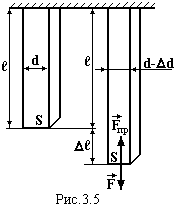

. (2.6)

Тут Е – модуль пружності, або модуль Юнга, вимірюється в Н/м². Він характеризує пружні властивості матеріалу і являється величиною сталою для кожного матеріалу.

Відношення абсолютної деформації до початкового розміру називається відносною деформацією 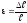, величина безрозмірна.

Відношення сили F до площі поперечного перерізу S називається механічною напругою , вимірюється в Н/м². Рівняння (2.6) приймає вигляд

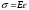. (2.7)

Це інша форма запису закона Гука.

З’ясуємо фізичний зміст модуля Юнга Е. При ε = 1, тобто коли ∆ℓ = ℓ, Е = σ. Отже, модуль Юнга, це така механічна напруга, при якій довжина стержня подвоїться. Значення модуля Юнга різних матеріалів можна знайти в довідникових таблицях.