
- •Лекции по математическому анализу для студентов первого курса Химфака мгу
- •Обозначения и логические символы
- •§ 1. Полнота множества действительных чисел
- •§ 2. Предел последовательности
- •§ 3. Предел монотонной и ограниченной последовательности. Число е
- •§ 4. Предел функции
- •Свойства бесконечно малых величин.
- •§ 5. Односторонние пределы. Предел монотонной и ограниченной функции
- •§ 6. Предел сложной функции
- •§ 7. Переход к пределу в неравенстве
- •§ 8. Предел
- •§ 9. Предел и три следствия из него
- •§ 10. Сравнение бесконечно малых величин
- •§ 11. Непрерывность функции в точке
- •§ 12. Типы разрывов функции в точке
- •§ 13. Непрерывность монотонной функции.
- •§ 14. Непрерывность обратной функции
- •§ 15. Непрерывность основных элементарных функций и обратных к ним
- •§ 16. Свойства функций непрерывных на отрезке
- •§ 17. Равномерная непрерывность. Теорема Кантора
- •§ 18. Производная функции в точке
- •§ 19. Дифференцирование обратной функции
- •§ 20. Дифференцирование сложной функции
- •§ 21. Дифференциал функции и его свойства
- •Свойства дифференциала
- •§ 22. Производные произвольных порядков. Формула Лейбница
- •§ 23. Теоремы о конечных приращениях
- •§ 24. Формула Тейлора
- •§ 25. Представление основных элементарных функций с помощью формулы Тейлора
- •§ 26. Правило Лопиталя
- •§ 27. Исследование функций Нахождение локального экстремума функции
- •Условия выпуклости функции
§ 17. Равномерная непрерывность. Теорема Кантора
Пусть
![]() числовое множество, которое является
либо отрезком
,
либо интервалом
,
либо полуинтервалом
числовое множество, которое является
либо отрезком
,
либо интервалом
,
либо полуинтервалом
![]() или
или
![]() ,
либо всей числовой прямой
,
либо объединением отрезков, интервалов
и полуинтервалов. Функция
определена на
,
либо всей числовой прямой
,
либо объединением отрезков, интервалов
и полуинтервалов. Функция
определена на
![]() .
.
Определение.
Функция
равномерно непрерывна на
,
если выполняются следующее условие:
такое, что
![]() .
.
Пример
1.
Функция
равномерно непрерывна на всей числовой
оси
.
Действительно, если выбрать
![]() ,
то условие определения равномерной
непрерывности будет выполнятся, так
как:
,
то условие определения равномерной
непрерывности будет выполнятся, так
как:

![]() .
.
Пример
2.
Функция
не является равномерно непрерывной на
![]() .
Действительно, пусть
и число
.
Действительно, пусть
и число
![]() так же задано. Выберем значения
так же задано. Выберем значения
![]() следующим образом
следующим образом
![]() ,
,
![]() ,
где
− натуральное число такое, что
,
где
− натуральное число такое, что
 или
или
![]() .
Тогда
.
Тогда
 ,
т.е. условие равномерной непрерывности
нарушается. Следовательно, функция
не является равномерно непрерывной на
.
Заметим, что если
равномерно непрерывна на
,
то она непрерывна в каждой точке множества
.
Как показывает пример 2, обратное
утверждение неверно. Однако, если
− есть отрезок, то справедлива
,
т.е. условие равномерной непрерывности
нарушается. Следовательно, функция
не является равномерно непрерывной на
.
Заметим, что если
равномерно непрерывна на
,
то она непрерывна в каждой точке множества
.
Как показывает пример 2, обратное
утверждение неверно. Однако, если
− есть отрезок, то справедлива
Теорема Кантора. Пусть . Тогда равномерно непрерывна на . (Без доказательства)
§ 18. Производная функции в точке
Пусть
определена в
![]() .
.
Определение.
Производной
![]() функции
в точке
называется предел:
функции
в точке
называется предел:
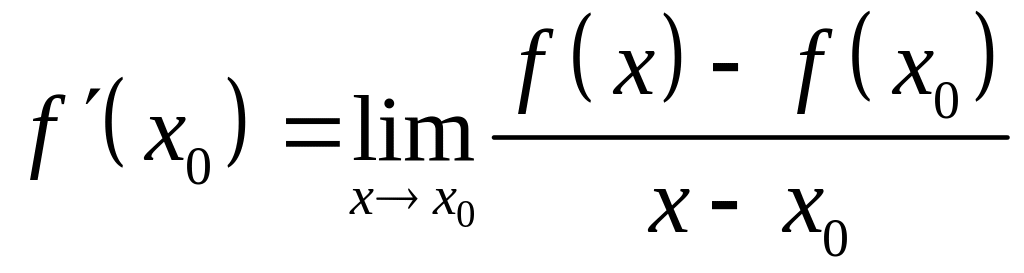 , (1)
, (1)
если
он существует. Обозначим
![]() ,
,
![]() .
Тогда равенство (1) эквивалентно равенству:
.
Тогда равенство (1) эквивалентно равенству:
![]() . (2)
. (2)
Определение.
Функцию
называют дифференцируемой в точке
,
если
![]() такое, что справедливо равенство:
такое, что справедливо равенство:
![]() . (3)
. (3)
Сравнивая
соотношения (2) и (3), получим
![]() .
Таким образом, если функция дифференцируема
в точке
,
то она имеет в точке производную
.
Таким образом, если функция дифференцируема
в точке
,
то она имеет в точке производную
![]() .
Верно и обратное: если
имеет в точке
производную, то она дифференцируема в
этой точке. Кратко будем записывать:
.
Верно и обратное: если
имеет в точке
производную, то она дифференцируема в
этой точке. Кратко будем записывать:
![]() .
Рассмотрим график функции
.
Обозначим
.
Рассмотрим график функции
.
Обозначим
![]() ,
точки
,
точки
![]() с координатами соответственно
с координатами соответственно
![]() .
Прямую, проходящую через точки
и
будем называть секущей графика. Тогда
угловой коэффициент секущей, т.е. тангенс
угла наклон секущей с осью
.
Прямую, проходящую через точки
и
будем называть секущей графика. Тогда
угловой коэффициент секущей, т.е. тангенс
угла наклон секущей с осью
![]() ,
равен
,
равен
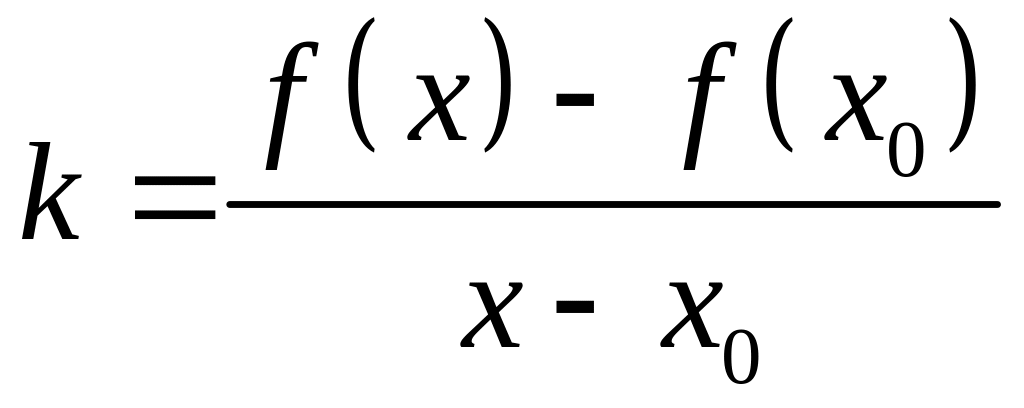 .
Предельное положение секущей, когда
.
Предельное положение секущей, когда
![]() ,
есть касательная к графику в точке
.
Таким образом, угловой коэффициент
касательной равен
,
есть касательная к графику в точке
.
Таким образом, угловой коэффициент
касательной равен
 ,
а уравнение самой касательной будет
,
а уравнение самой касательной будет
![]() .
.
Производная суммы, произведения и частного двух функций:
1) ![]() ;
2)
;
2) ![]() ;
3) если
;
3) если ![]() , то
, то  .
Доказательство:
1)
.
Доказательство:
1) 
 ;
2)
;
2) 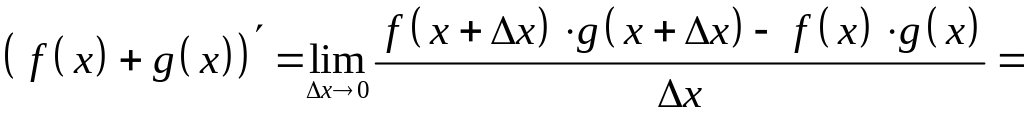

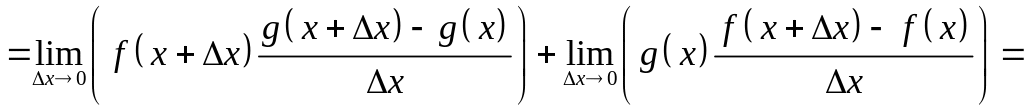
![]() ;
3) Пусть
;
3) Пусть ![]() . Тогда
. Тогда 
 .
Далее,
применяя доказанное правило
дифференцирования произведения
функций, получим соотношение:
.
Далее,
применяя доказанное правило
дифференцирования произведения
функций, получим соотношение:

 .
.
§ 19. Дифференцирование обратной функции
Утверждение.
Пусть
определена
,
строго монотонна и непрерывна,
и
![]() .Тогда
в
.Тогда
в
![]() ,
где
определена обратная функция
также строго монотонная,
непрерывная,
,
где
определена обратная функция
также строго монотонная,
непрерывная, ![]() и
и  .
Доказательство.
Существование и непрерывность обратной
функции было доказано ранее. Далее
имеем:
.
Доказательство.
Существование и непрерывность обратной
функции было доказано ранее. Далее
имеем:
 .
.
§ 20. Дифференцирование сложной функции
Утверждение.
Пусть
определена
,
,
а
определена в
,
,
.
Тогда
![]() и
и ![]() .
Доказательство. Так как
и
, то:
.
Доказательство. Так как
и
, то:
![]() и
и
![]() .
.
Из
этих соотношений по свойствам б.м.в.
следует, что:
![]()
![]() .
Утверждение
доказано.
.
Утверждение
доказано.
Производные основных элементарных функций и обратных к ним: Используя доказанные выше свойства производных и пределов, докажем следующие равенства:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4) ![]() ;
5)
;
5) ![]() ;
6)
;
6) ![]() ;
7)
;
7) ![]() ;
8)
;
8)  ;
9)
;
9)  ;
10)
;
10) ![]() ;
11)
;
11) ![]() ;
12)
;
12) ![]() 13)
13) ![]() ;
;
Доказательства:
1) 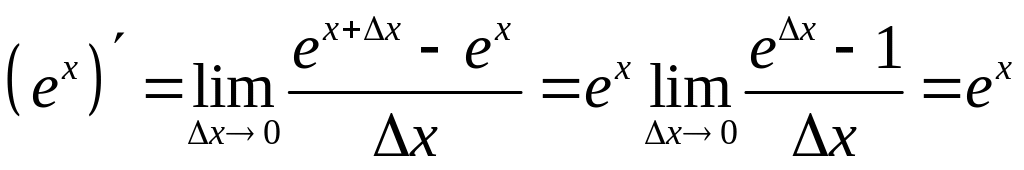 ;
2)
;
2) ![]() ;
3)
;
3)  ;
4)
;
4)  ;
5)
;
5)  ;
другое
доказательство:
;
другое
доказательство:
 ;
6)
;
6)  ;
7)
;
7) ![]() ;
8)
;
8) 
 , т.к.
, т.к. ![]() ;
9)
;
9)  ;
10)
;
10)  ;
11)
;
11)  ;
12)
;
12)  ;
13)
;
13)  ;
;
