
- •Лекции по математическому анализу для студентов первого курса Химфака мгу
- •Обозначения и логические символы
- •§ 1. Полнота множества действительных чисел
- •§ 2. Предел последовательности
- •§ 3. Предел монотонной и ограниченной последовательности. Число е
- •§ 4. Предел функции
- •Свойства бесконечно малых величин.
- •§ 5. Односторонние пределы. Предел монотонной и ограниченной функции
- •§ 6. Предел сложной функции
- •§ 7. Переход к пределу в неравенстве
- •§ 8. Предел
- •§ 9. Предел и три следствия из него
- •§ 10. Сравнение бесконечно малых величин
- •§ 11. Непрерывность функции в точке
- •§ 12. Типы разрывов функции в точке
- •§ 13. Непрерывность монотонной функции.
- •§ 14. Непрерывность обратной функции
- •§ 15. Непрерывность основных элементарных функций и обратных к ним
- •§ 16. Свойства функций непрерывных на отрезке
- •§ 17. Равномерная непрерывность. Теорема Кантора
- •§ 18. Производная функции в точке
- •§ 19. Дифференцирование обратной функции
- •§ 20. Дифференцирование сложной функции
- •§ 21. Дифференциал функции и его свойства
- •Свойства дифференциала
- •§ 22. Производные произвольных порядков. Формула Лейбница
- •§ 23. Теоремы о конечных приращениях
- •§ 24. Формула Тейлора
- •§ 25. Представление основных элементарных функций с помощью формулы Тейлора
- •§ 26. Правило Лопиталя
- •§ 27. Исследование функций Нахождение локального экстремума функции
- •Условия выпуклости функции
§ 9. Предел и три следствия из него
Утверждение. ![]() .
Доказательство.
Определение.
Целой частью числа
(обозначается
.
Доказательство.
Определение.
Целой частью числа
(обозначается
![]() )
называется
наибольшее целое число, не превосходящее
.
Пример.
)
называется
наибольшее целое число, не превосходящее
.
Пример. ![]() .
Пусть
.
Пусть
![]() .
Обозначим
.
Обозначим
 .
Тогда, из определения целой части числа
следует, что
.
Тогда, из определения целой части числа
следует, что
![]()
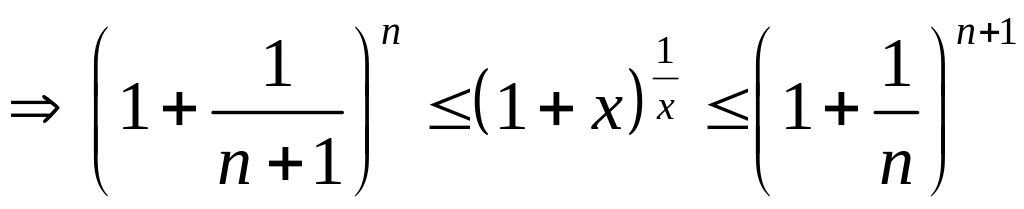 .
Применим к этому неравенству лемму о
двух милиционерах. Так как
.
Применим к этому неравенству лемму о
двух милиционерах. Так как
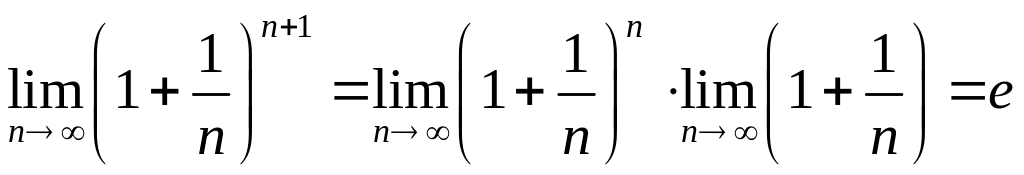 и
и
 , то
, то ![]() Далее
докажем, что
Далее
докажем, что
![]() .
Пусть
.
Пусть
![]() .
Обозначим
.
Обозначим
![]() .
Тогда ввиду равенств
.
Тогда ввиду равенств
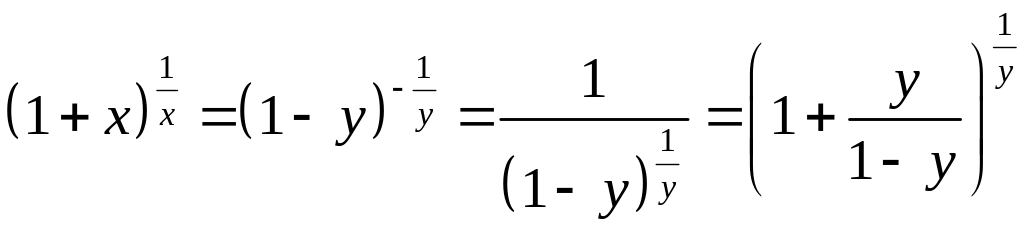 ..
Обозначим
..
Обозначим
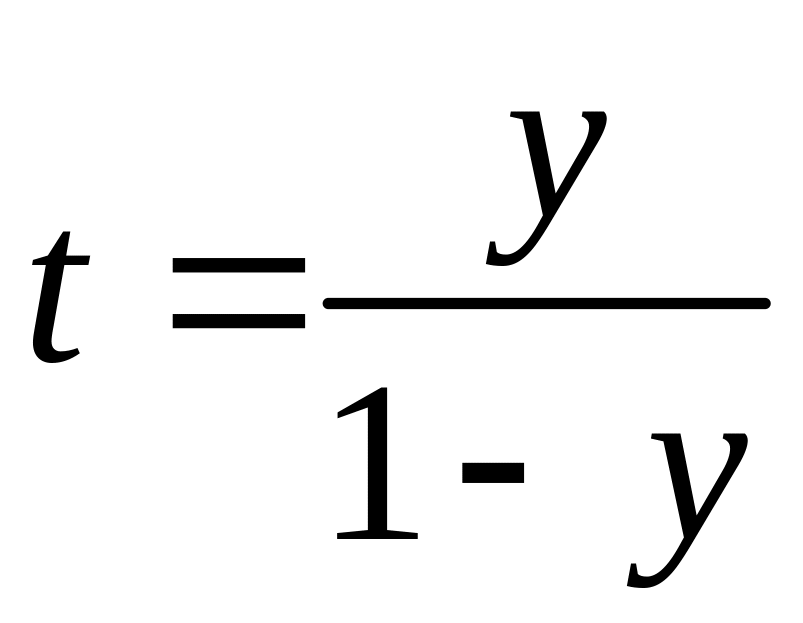 .
Тогда
.
Тогда
![]() и
и
![]() при
при
![]() ,
,
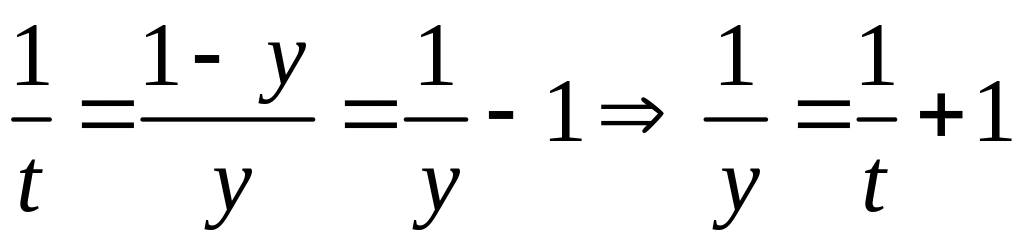 .
Следовательно, получаем соотношение
.
Следовательно, получаем соотношение
![]() и
и
![]() .
Итак, мы доказали, что
.
Итак, мы доказали, что
![]() ,
т.е.
,
что и требовалось доказать.
,
т.е.
,
что и требовалось доказать.
Из доказанного утверждения выведем три важных предела:
1) 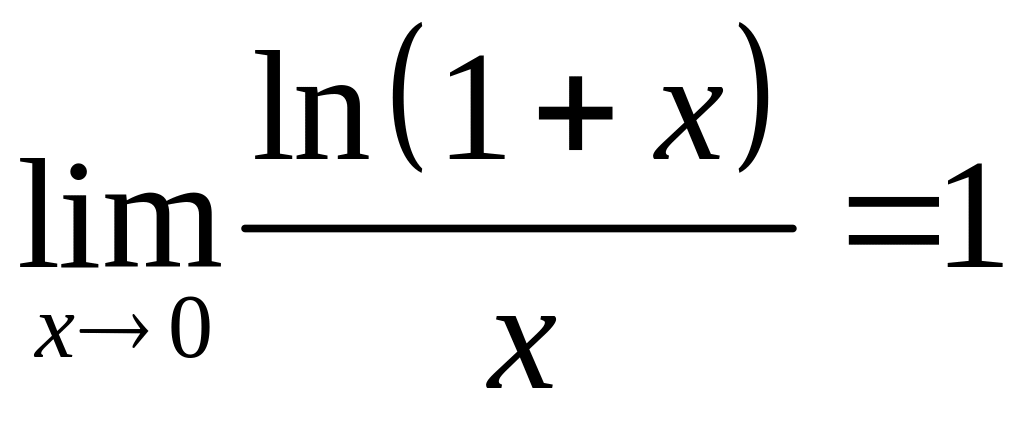 ;
2)
;
2) 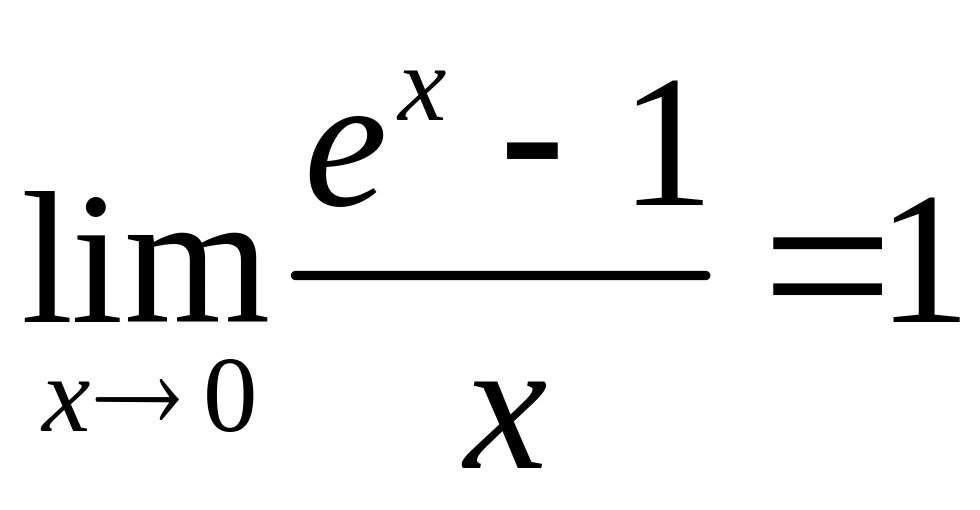 ;
3)
;
3) 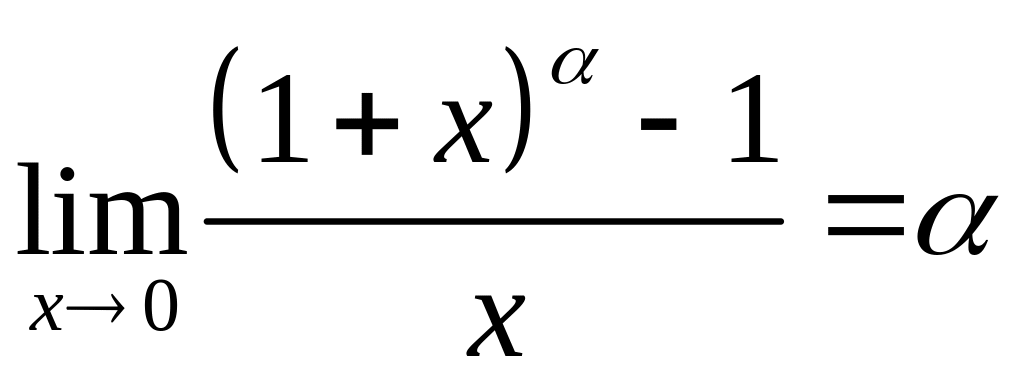 .
Доказательства:
1)
.
Доказательства:
1) 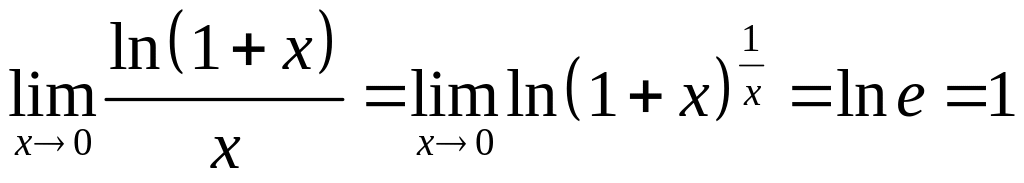 ;
2)
;
2)  ;
3)
;
3) 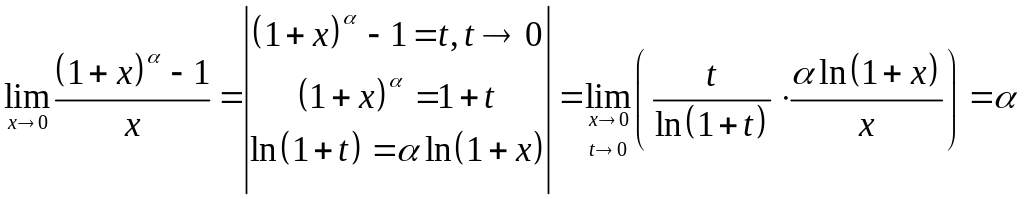 .
Правомерность
этих предельных переходов следует из
непрерывности функций
.
Правомерность
этих предельных переходов следует из
непрерывности функций
![]() и
и
![]() ,
что будет доказано далее.
,
что будет доказано далее.
§ 10. Сравнение бесконечно малых величин
Будем предполагать, что функции, которые мы будем рассматривать в этом параграфе определены в окрестности нуля.
Определение.
Функция
есть
![]() (о-малое от функции
),
если
(о-малое от функции
),
если
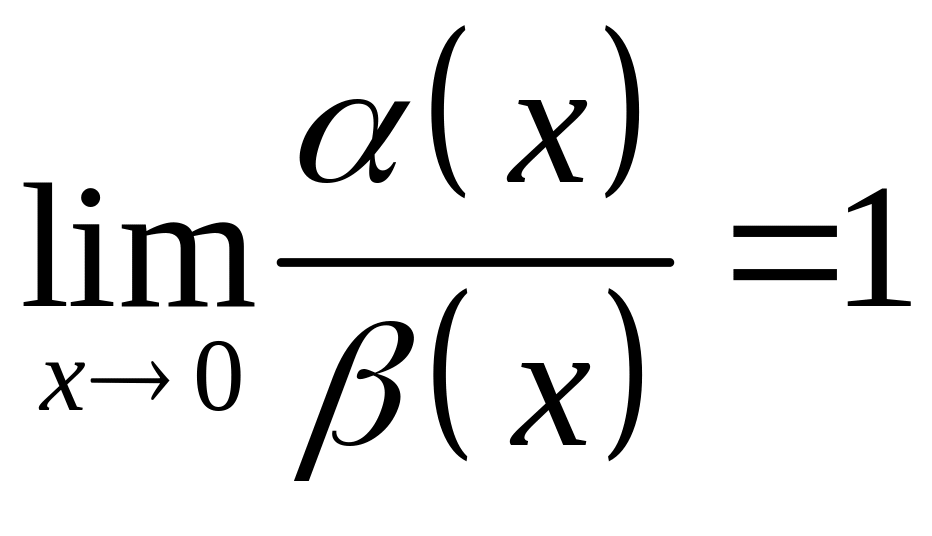 .
Запись
.
Запись
![]() ,
.т.е.
− бесконечно малая величина.
,
.т.е.
− бесконечно малая величина.
Свойства бесконечно малых величин:
1) если ![]() , то
, то ![]() ;
2)
;
2) ![]() ,
если
,
если
![]() (символ “
(символ “![]() ”
означает, что
левую часть равенства можно заменить на правую);
3)
”
означает, что
левую часть равенства можно заменить на правую);
3) ![]() ;
4)
;
4) ![]() ;
5) если
;
5) если ![]() , то
, то 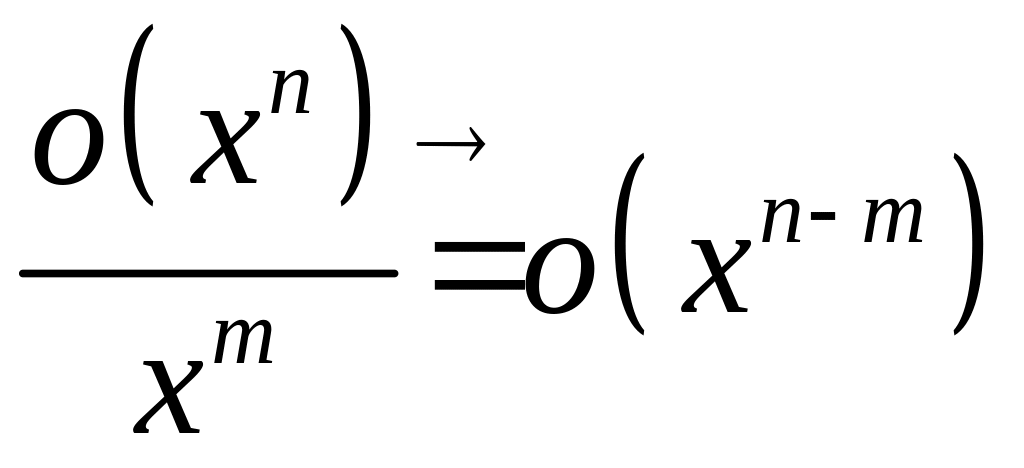 ;
6)
;
6) ![]() ;
7)
;
7) ![]() .
Доказательство.
Докажем два первых свойства. Доказательство
остальных предлагаем сделать самостоятельно.
1) Пусть
.
Доказательство.
Докажем два первых свойства. Доказательство
остальных предлагаем сделать самостоятельно.
1) Пусть
![]() .
Тогда по определению о-малого:
.
Тогда по определению о-малого:
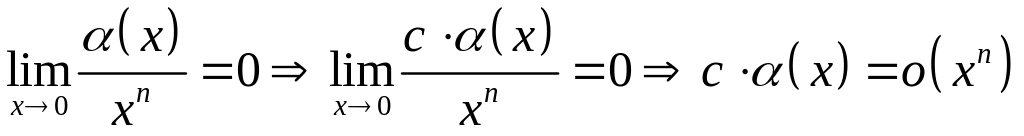 .
Свойство 1 доказано.
2)
Пусть
и
.
Свойство 1 доказано.
2)
Пусть
и
![]() ,
,
,
,
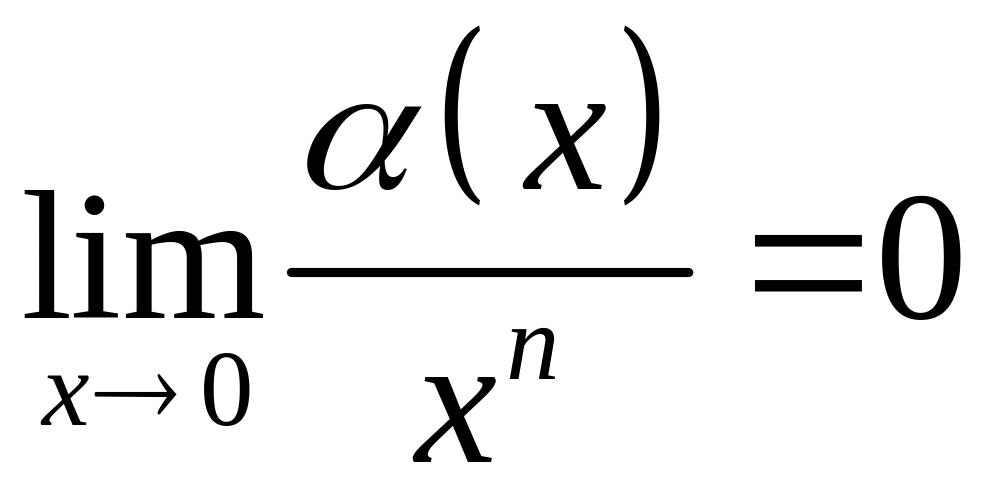 и
и
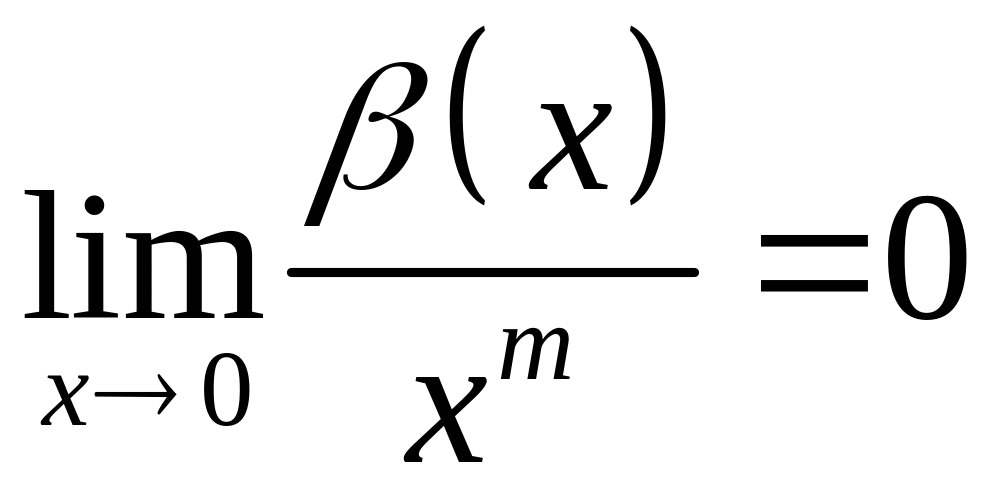 ,
тогда
,
тогда
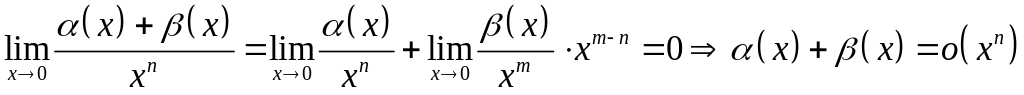 ,
что и требовалось доказать.
,
что и требовалось доказать.
Примеры:
1) ![]() ;
2)
;
2)  ;
3)
;
3) 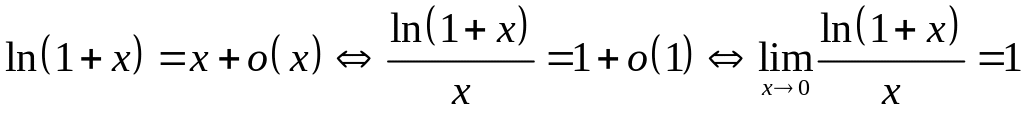 ;
4)
;
4) 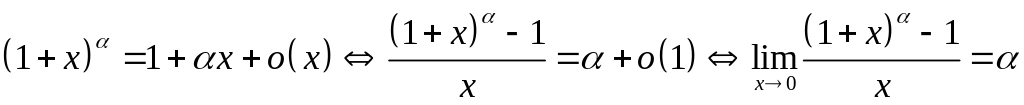 .
.
Свойства бесконечно малых величин удобно применять при вычислении пределов.
§ 11. Непрерывность функции в точке
Пусть
функция
определена в
![]() ,
окрестности точки
.
,
окрестности точки
.
Определение.
Функция
непрерывна в точке
(краткая запись:
![]() ),
если
),
если
![]() .
.
Свойства непрерывных в точке функций:
1)
Если
![]() ,
то
,
то
![]() и
и
![]() ;
кроме того, если
;
кроме того, если ![]() , то
, то 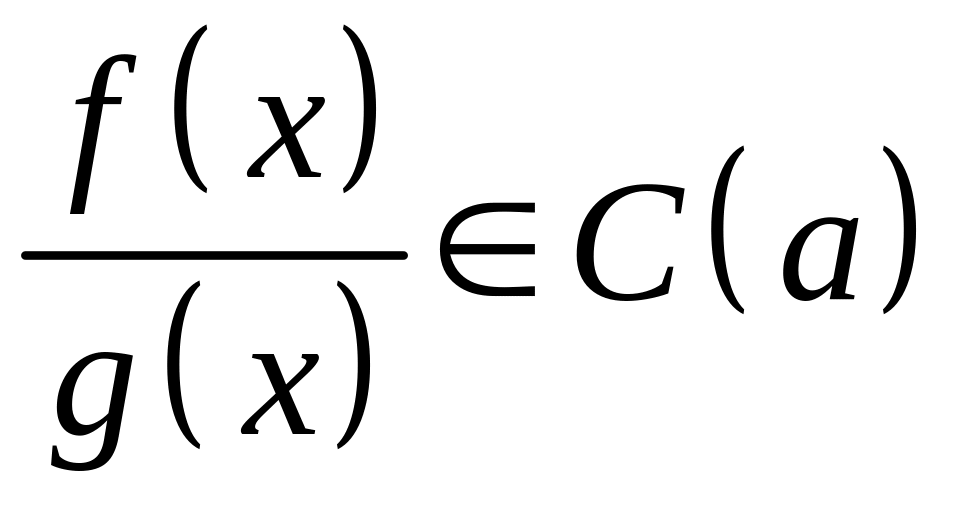 .
2) Если
.
2) Если ![]() , то
, то ![]() .
Доказательство
свойства 1 получается, если воспользоваться
соответствующими свойствами пределов функции.
Для
доказательства свойства 2 нужно применить
теорему о пределе сложной функции.
.
Доказательство
свойства 1 получается, если воспользоваться
соответствующими свойствами пределов функции.
Для
доказательства свойства 2 нужно применить
теорему о пределе сложной функции.
§ 12. Типы разрывов функции в точке
Определение.
Функция
имеет в точке
устранимый разрыв, если
и
![]() или значение
не определено.
или значение
не определено.
Пример.
![]() .
Значение
.
Значение
![]() не определено. Если мы определим
не определено. Если мы определим
![]() ,
то функция
станет непрерывной в точке
,
то функция
станет непрерывной в точке
![]() .
.
Определение.
Функция
имеет в точке
разрыв первого рода, или скачок, если
![]() ,
,
![]() и
и
![]() .
.
Пример.
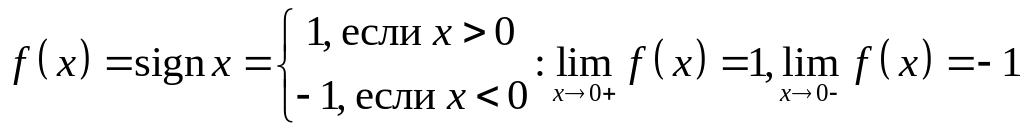 .
.
Определение.
Функция
имеет в точке
разрыв второго рода, если не существует
хотя бы один из односторонних пределов
![]() или
или
![]() .
.
Примеры:
1) ![]() при
;
2)
при
;
2) ![]() при
;
3)
при
;
3) 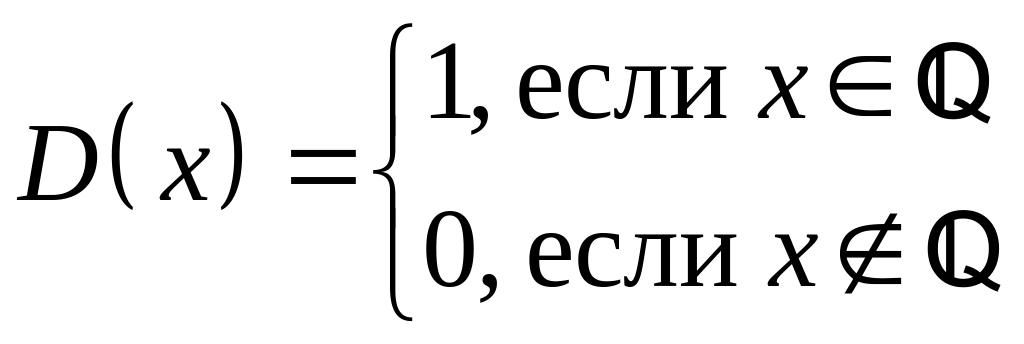 − функция Дирихле.
В
первых двух примерах точка
является точкой разрыва второго рода.
В третьем примере функция
− функция Дирихле.
В
первых двух примерах точка
является точкой разрыва второго рода.
В третьем примере функция
![]() имеет разрыв второго рода в любой точке
(доказать самостоятельно).
имеет разрыв второго рода в любой точке
(доказать самостоятельно).
§ 13. Непрерывность монотонной функции.
Определение.
Функция
непрерывна справа (слева) в точке
,
если
![]() (соответственно
(соответственно
![]() ).
).
Определение.
Функция
непрерывна на отрезке
![]() ,
если
,
,
если
,
![]() ,
кроме того
непрерывна справа в точке
и непрерывна в точке
.
,
кроме того
непрерывна справа в точке
и непрерывна в точке
.
Теорема.
Пусть функция
определена на отрезке
и монотонна, т.е. не убывает или не
возрастает на
.
Кроме того функция
принимает все промежуточные значения
между
и
![]() .
Тогда
.
Тогда
![]() .
Доказательство.
По теореме о пределе монотонной функции
и
.
Пусть для определённости функция
не убывает, тогда:
.
Доказательство.
По теореме о пределе монотонной функции
и
.
Пусть для определённости функция
не убывает, тогда:
![]() ,
,
![]() .
Переходя к пределу в неравенстве
получаем:
.
Переходя к пределу в неравенстве
получаем:
![]() .
Если
.
Если
![]() ,
то выберем число
так, чтобы
,
то выберем число
так, чтобы
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
что противоречит предположению теоремы.
Следовательно,
,
что противоречит предположению теоремы.
Следовательно,
![]() и
и
![]() .
Аналогично доказывается, что
непрерывна слева в точке
и
непрерывна справа в точке
(доказать самостоятельно). Теорема
доказана.
.
Аналогично доказывается, что
непрерывна слева в точке
и
непрерывна справа в точке
(доказать самостоятельно). Теорема
доказана.
Следствие. Из доказательства теоремы следует, что, если монотонна на , то либо , либо имеет в точке разрыв первого рода (скачок).
