§ 5. Односторонние пределы. Предел монотонной и ограниченной функции

Определение. Число называется пределом справа функции в точке , или , если такое, что .

Аналогично определяется предел слева. Число называется пределом слева функции в точке , или , если такое, что .

Из определений пределов следует

утверждение.  .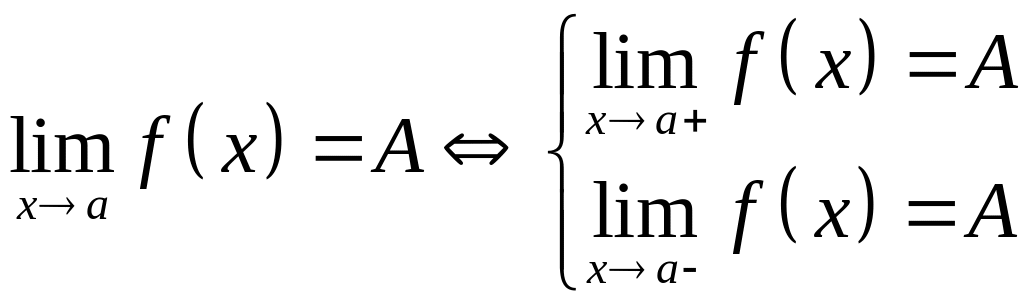

В качестве примера рассмотрим функцию: .

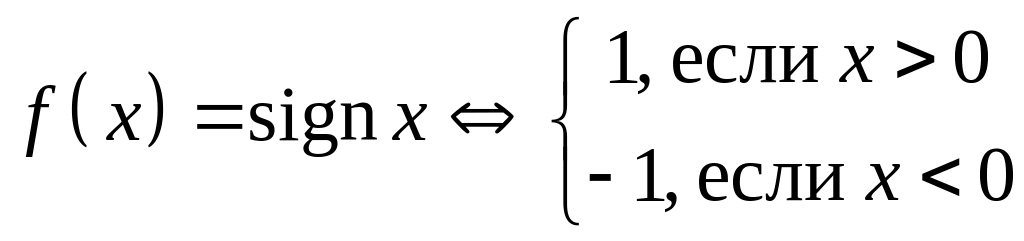Справедливы равенства , .

Определения:

Функцию будем называть неубывающей (невозрастающей) на интервале , если (или ).

Функцию будем называть возрастающей (невозрастающей) на интервале , если (или ).

Функцию будем называть монотонной на , если она неубывающая или невозрастающая на .

Функцию будем называть строго монотонной на , если она возрастает или убывает на .

Функцию будем называть ограниченной на , если множество её значений ограничено.

Утверждение. Пусть функция монотонна и ограничена на , тогда и . Кроме того, и . Доказательство. Пусть функция неубывающая, точка . Докажем, что . Рассмотрим множество . По условию ограничено, следовательно, по аксиоме 1 полноты . Обозначим и докажем, что . Действительно, из того, что следует: . Обозначим , тогда ввиду неубывания функции  :  . Мы доказали, что . Аналогично доказывается , , . Доказательство этих утверждений предлагаем сделать самостоятельно, а также рассмотреть случай невозрастающей функции.

§ 6. Предел сложной функции

Теорема о пределе сложной функции. Пусть функция определена в , а функция в ; кроме того , , , тогда  . Доказательство. Пусть задано число . По определению предела такое, что . Заметим, что при . Далее, так как , то такое, что . Пусть , тогда , что и доказывает теорему.

Замечание. Условие теоремы нельзя отбросить, как показывает следующий пример: при , где можно показать, что , , а не существует. Предлагаем доказать это самостоятельно.

§ 7. Переход к пределу в неравенстве

Утверждение 1. Пусть функции и определены в , , , , , тогда . Доказательство. Пусть . Выберем число , тогда, по определению предела функции такое, что 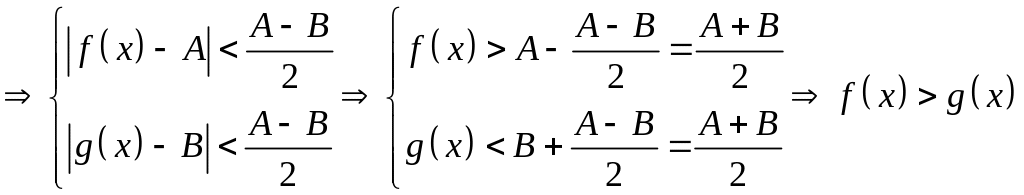, что противоречит условию . Следовательно . Утверждение 1 доказано.

Утверждение 2 (лемма о двух милиционерах). Пусть функции , и определены в , , , , тогда  . Доказательство. Рассмотрим 2 случая: 1) Пусть , тогда по определению предела функции такое, что: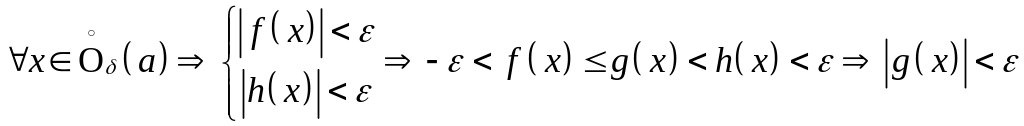 . Следовательно,  . 2) Пусть , тогда обозначим , , . Функции удовлетворяют неравенствам и . Следовательно по доказанному выше , что и требовалось доказать.

§ 8. Предел

У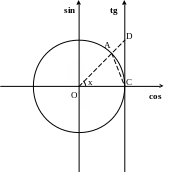 тверждение.  . Доказательство. Пусть 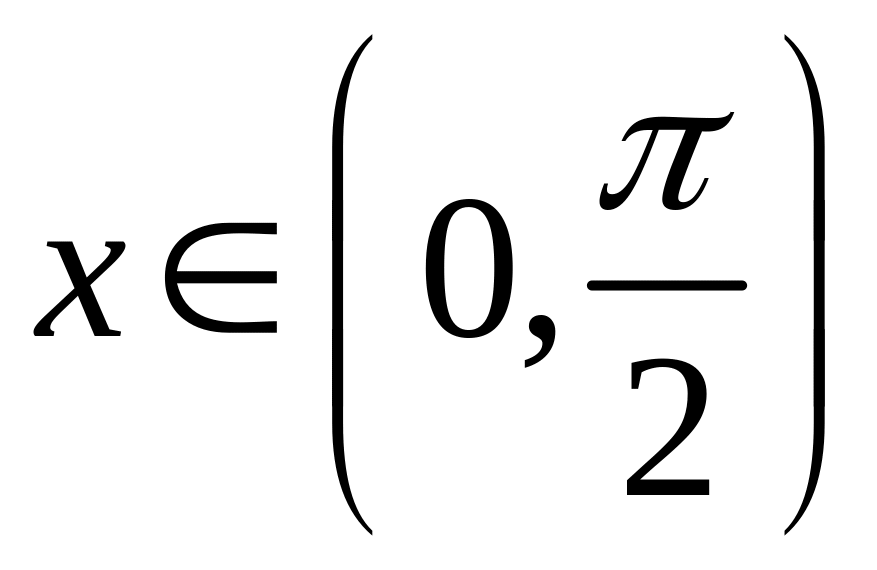 . Рассмотрим окружность единичного радиуса с центром . Луч, выходящий из центра под углом радиан к оси пересекает окружность в точке , а ось в точке . Площадь треугольника не превосходит площади сектора , которая в свою очередь не превосходит площади треугольника  , т.е.  . Последнее неравенство, ввиду чётности функций и справедливо для всех . Заметим, что , т.к. . Следовательно, переходя к пределу в неравенстве , получим требуемое утверждение.