§ 4. Предел функции

Определения: Окрестностью точки будем называть произвольный открытый интервал, содержащий точку , и обозначать . Проколотой окрестностью точки будем называть окрестность точки , из которой исключена сама точка , и обозначать . δ-окрестностью точки будем называть такую окрестность точки , что , т.е. множество точек расположенных на действительной прямой на расстоянии от точки меньшем, чем . Проколотой δ-окрестностью точки будем называть множество , т.е. – δ-окрестность точки , из которой исключена сама точка .

Пусть функция определена в некоторой .

Определение предела функции. Число называется пределом функции при стремящемся к , или , если выполнено следующее условие: такое, что .

Замечание. В определении предела функции в точке не учитывается значение функции в самой точке . В частности, значение может отличаться от или быть вовсе не определено.

Определение бесконечно малой величины (б.м.в.). Функция называется бесконечно малой величиной (сокращенно б.м.в.) в точке , если .

Утверждение. , где есть б.м.в. в точке .

Это утверждение следует из определений предела функции и б.м.в., ввиду эквивалентности неравенств: .

Определение. Функцию будем называть локально ограниченной в точке , если такие, что или (эквивалентное условие) если такая, что .

Утверждение. Если , то локально ограничена в точке . Доказательство. Так как в определении предела функции число может быть выбрано произвольно, то положим , тогда такое, что . Следовательно, функция локально ограничена. Утверждение доказано.

Свойства бесконечно малых величин.

Утверждение. Пусть и − б.м.в., а локально ограничена в точке . Тогда , и − б.м.в. Доказательство. Докажем, что − б.м.в. в точке .По определению б.м.в. и . Пусть выбрано число . Тогда и такие, что ,  . Пусть  , тогда 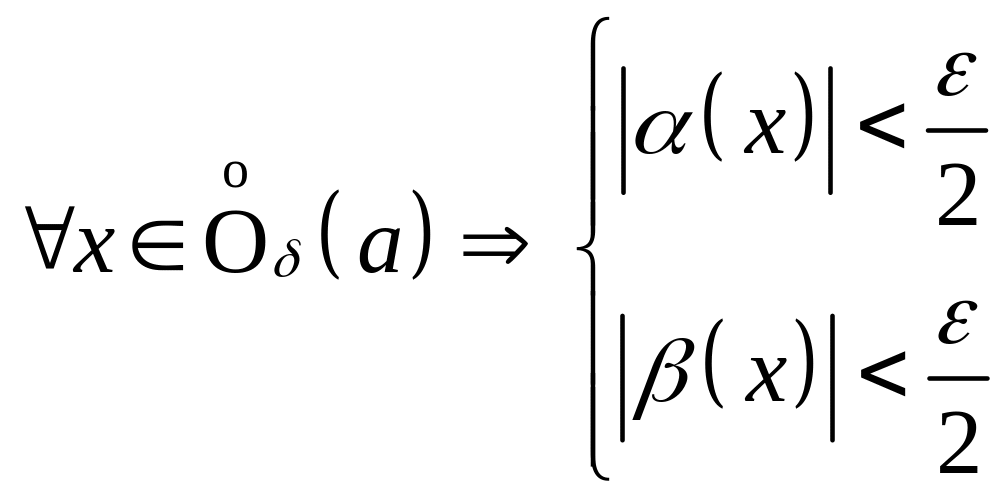 . Следовательно , т.е. , по определению предела это означает, что  − б.м.в. в точке  . Далее докажем, что − б.м.в. в точке . Пусть задано число . Так как локально ограничена в точке , то такая, что . Далее, по определению предела функции такое, что . Следовательно, , т.е. , и тем самым доказано, что   − б.м.в. в точке  . Осталось доказать, что − б.м.в. в точке . Так как , то локально ограничена в точке по доказанному выше утверждению. Следовательно, − б.м.в. в точке .

Арифметические свойства предела функции. Пусть в некоторой заданы функции и такие, что и , тогда выполняются следующие равенства: 1)  2)  3) если  , то  . Доказательство. Так как по доказанному выше: , где и − б.м.в. в точке , то:

.

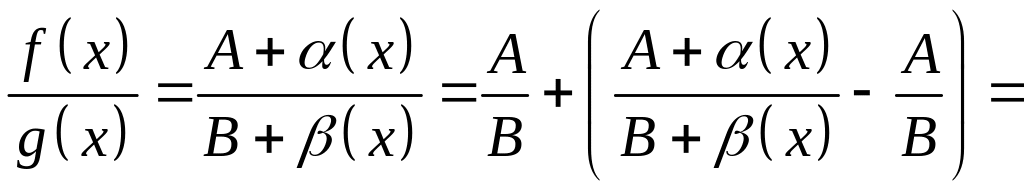
По свойствам б.м.в. и есть б.м.в. в точке . Следовательно, справедливы свойства 1) и 2). Для доказательства свойства 3) заметим, что при функция локально ограничена (доказать самостоятельно). Далее представим частное функций   и   в следующем виде: По свойствам б.м.в. есть б.м.в., следовательно свойство 3) также доказано.