§ 27. Исследование функций Нахождение локального экстремума функции

Доказанная ранее теорема Ферма устанавливает необходимое условие локального экстремума функции в точке , если .

Теорема 1 (достаточное условие локального экстремума). Пусть и . Кроме того, , а . Тогда в точке функция имеет строгий локальный экстремум, причем если , то – точка строгого локального максимума.

Доказательство. Запишем формулу Тейлора для :

, или .

Т.к. по условию теоремы , знак правой части последнего равенства в достаточно малой окрестности определяется знаком числа . Поэтому, если , то , т.е. – точка строгого локального минимума, а если , то аналогично – точка строгого локального максимума. Теорема 1 доказана.

Замечание. Если , то теорема 1 не позволяет установить является ли точка точкой локального экстремума.

Следующая теорема обобщает результат теоремы 1.

Теорема 2. Пусть и . Кроме того, , а . Тогда если четно, то – точка строгого локального экстремума, причем, если , то – точка строгого локального минимума, а если , то – точка строгого локального максимума. Если же нечетно, то в точке функция не имеет локального экстремума. Доказательство. Представим по формуле Тейлора:

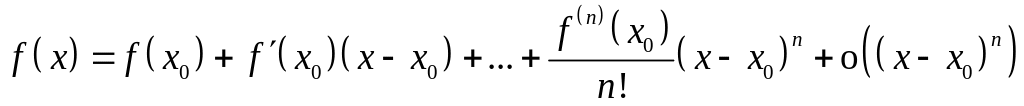, или

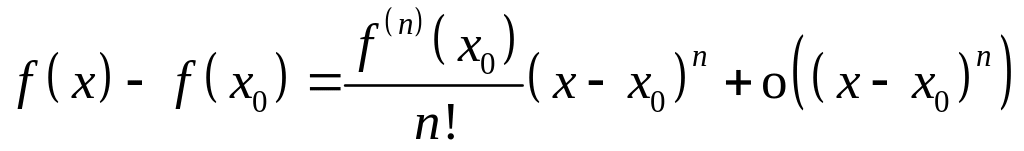. (1)

Если четно, то знак правой части равенства (1) в достаточно малой окрестности определяется знаком . Следовательно, если ,то , т.е. – точка строгого локального минимума; если , то , т.е. – точка строгого локального максимума. Если же число нечетно, то значения правой части равенства (1) имеет разные знаки в правой и левой полуокрестностях точки. Следовательно, точка не является точкой локального экстремума. Теорема 2 доказана.

Условия выпуклости функции

Пусть .

Определение. Функция выпукла вверх в точке , если:

,

и выпукла вниз, если:

.

Геометрически условия выпуклости означает, что если выпукла вверх в точке , то график функции лежит ниже графика касательной к этой функции в точке , когда ; и если выпукла вниз в точке , то график функции лежит выше графика касательной к этой функции в точке , когда .

Теорема 1. Пусть , и . Тогда, если , то выпукла вниз в точке ; если , то выпукла вверх в точке  . Доказательство. Воспользуемся формулой Тейлора для :

, или .

Знак правой части последнего равенства в достаточно малой окрестности определяется знаком числа . Поэтому, если , то: или т.е. – точка выпуклости вниз . Аналогично, если , то аналогично – точка выпуклости вверх . Теорема 1 доказана.

Определение. Точка есть точка перегиба функции , если знак выражения разный для точек, принадлежащих левой и правой полуокрестностям точки . Геометрически это означает, что график функции в левой и правой полуокрестностях точки лежит по разные стороны от касательной в точке .

Теорема 2. Пусть и . Кроме того, , а . Тогда если нечетно, то – точка перегиба; если число четное, то при функция выпукла вниз в точке , а при функция выпукла вверх в точке  . Доказательство. Воспользуемся формулой Тейлора для :

, или .

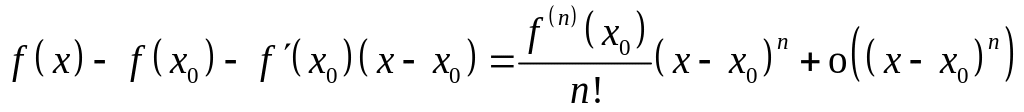Если нечетное, то знак выражения в правой части последнего равенства различный в левой и правой полуокрестностях точки – точка перегиба. Если число четное, знак правой части этого равенства в достаточно малой окрестности точки определяется знаком . Поэтому, если  ,то: , т.е. функция выпукла вниз в точке  , а если  , то: , т.е. функция выпукла вверх в точке . Теорема 2 доказана.

Cin

A

56