Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем

Целочисленное деление 3 7 1

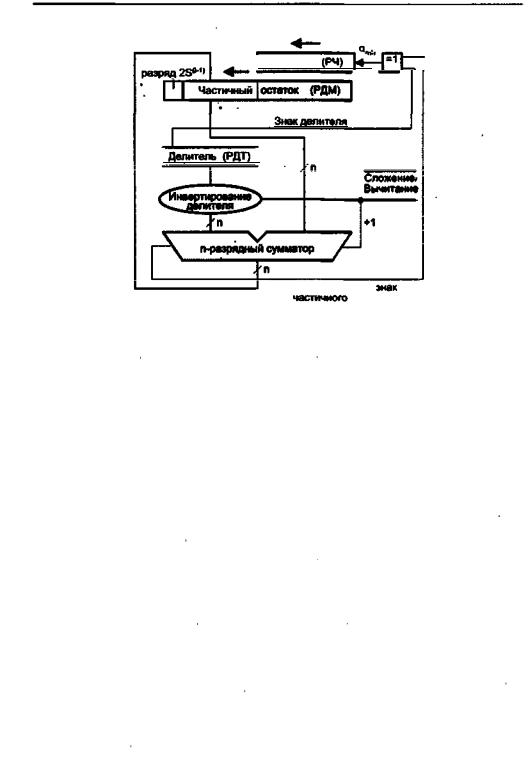
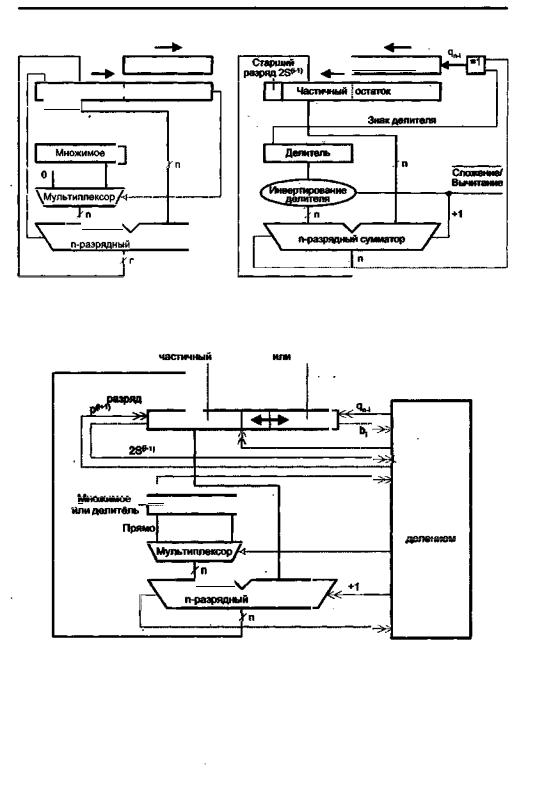
тель с сумматором одинарной длины. Неподвижный делитель D хранится в регис­ тре одинарной длины, а делимое Z, сдвигаемое относительно D, находится в двух таких же регистрах. Образующиеся цифры частного Q заносятся в освобождаю­ щиеся при сдвиге Z разряды одного из регистров Z

Ниже на. примере чисел без знака рассматриваются два основных алгоритма целочисленного деления.

Деление с восстановлением остатка

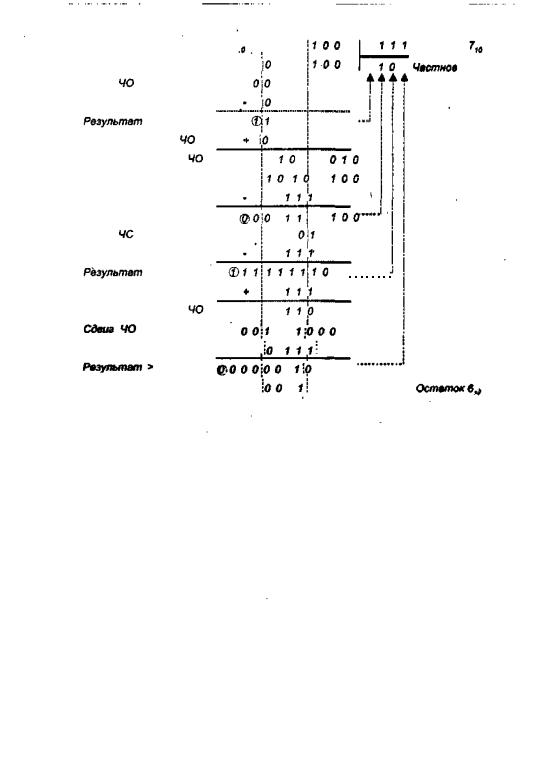
Наиболее очевидный алгоритм носит название алгоритма деления с неподвижным делителем и восстановлением остатка. В учебнике он представлен в силу того, что очень похож на общепринятый способ деления столбиком. Данный алгоритм мо­ жет быть описан следующим образом:

1. Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2.Частичный остаток удваивается путем сдвига на один разряд влево. При этом

восвобождающийся при сдвиге младший разряд 40 заносится очередная цифра частного.

3.Из сдвинутого Ч0 вычитается делитель и анализируется знак результата вы­ читания.

4.Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и нулю, если отрицателен. В последнем случае значение остатка восстанавливается до того значения, которое было до вычитания.

5.Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

На рис. 7,48 показан процесс деления с восстановлением остатка, здесь число 41 делится на 8.

Деление без восстановления остатка

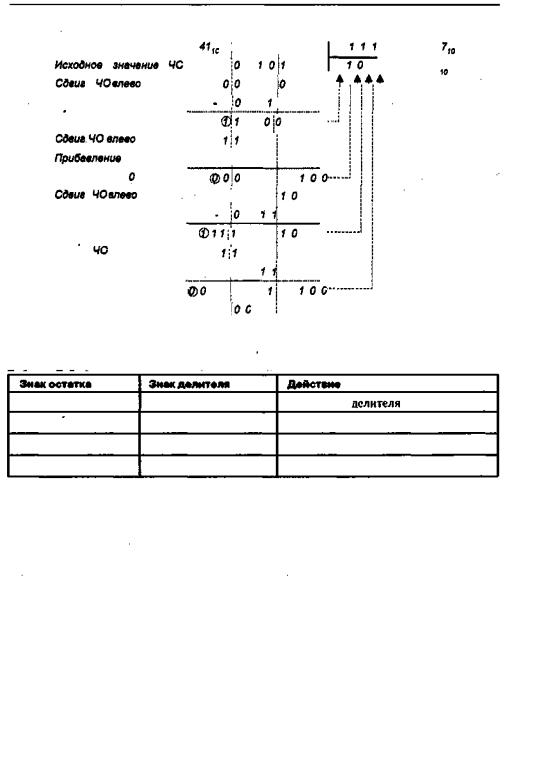
Недостаток затронутого алгоритма заключается в необходимости выполнения на отдельных шагах дополнительных операций сложения для восстановления час­ тичного остатка. Это увеличивает время выполнения деления, которое в этом слу­ чае может меняться в зависимости от конкретного сочетания кодов операндов. В силу указанных причин реальные делители строятся на основе алгоритма деле­ ния с неподвижным делителем без восстановления остатка. Приведем описание этого алгоритма.

1, Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2, Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разрядЧ0 заносится очередная цифра частного.

3, Из сдвинутого частичного остатка вычитается делитель, если остаток положи­ телен, и к сдвинутому частичному остатку прибавляется делитель, если оста­ ток отрицательный.