Дифференцируя это выражение, найдем

Подставляя сюда (7,5) и приводя подобные члены, получим дифференциальное уравнение

(7.7)

Здесь следует полагать _m=₀ = 0.

Применим полученное уравнение для решения следующей задачи [5]. Производственная информация накапливается и хранится в базе данных ЭВМ. Интенсивность пуассоновского потока поступления единиц информации в базу данных равна (t) и не зависит от того, сколько их уже накоплено. Принятая на хранение, единица информации, хранится некоторое время, после чего по определенному признаку исключается. Поток исключений для каждой единицы информации - пуассоновский с интенсивностью (t).

Дифференциальное уравнение (7,7) для математического ожидания числа единиц информации, находящихся в базе данных, принимает вид

Учитывая, что , получаем

Если интенсивности пополнения и исключения информации постоянны, то при начальном условии m_x (0) = m₀, решение уравнения имеет вид

В стационарном режиме

Сведения о дисперсии численности популяции можно найти в [5].

7.4. Циклический процесс

Рассмотрим процесс в системе, граф состояний которой изображен на рис. 7.4. Соответствующие дифференциальные уравнения таковы

Финальные вероятности состояний в стационарном режиме найдутся из системы:

Отсюда

Рис. 7.4.

Из условия нормировки определяется p₀

Примером циклического процесса может служить регулярно повторяемая транспортная или технологическая операция.

 

Глава 8 Метод динамики средних

 

8.1. Дифференциальные уравнения динамики средних

Рассмотрим систему S, состоящую из N однотипных элементов E, например, танковую роту. Пусть каждый из элементов может находиться в n различных состояниях. Ясно, что общее число различных состояний системы S равно n^N, и если N или n велико, то граф состояний системы будет необычайно громоздким, а решение уравнений Колмогорова затруднено даже на ЭВМ. Кроме того, результаты решения будут трудно обозримыми. Поэтому поставим задачу по-иному. Будем анализировать состояния отдельного элемента E, а также средние характеристики системы S.

Обозначим возможные состояния элемента E символами ₁, ₂,...,_n. Состояние системы в целом в момент времени t будем характеризовать числом элементов X_k(t), находящихся в состоянии _k. Ясно, что X_k(t), k=1,2,...,n - случайные функции времени. Их математические ожидания и дисперсии равны

(8.1)

 

где p_k (t) - вероятность того, что в момент времени t отдельный элемент системы будет находится в состоянии  _k.

Дифференциальные уравнения Колмогорова для вероятностей состояний элементов имеют вид

 

( 8.2)

 

Умножая эту систему на число элементов N и принимая во внимание (8,1), получим дифференциальные уравнения динамики средних:

 

(8.3)

 

Для однозначного решения этой системы одно из ее уравнений должно быть заменено нормирующим условием

 

 

В общем случае интенсивности потоков событий _jk, переводящих элементы системы их одного состояния в другие, зависят от того, сколько элементов в данном состоянии имеется в системе. Численности X_j(t) и X_k (t) случайны, поэтому случайными оказываются и интенсивности переходов. Это затруднение преодолевается за счет допущения, носящего название принципа квазирегулярности. Принимается, что интенсивность потоков событий зависит не от самих численностей состояний, а от их средних значений (математических ожиданий):

 

 

Уравнения динамики средних (8,3) могут быть обобщены на случай, когда в ходе моделируемого процесса происходит пополнение системы S извне элементами, находящимися в том или ином состоянии. Если интенсивность пополнения системы элементами k-ого состояния обозначить  _k(t), то уравнения (8,3) следует переписать в виде

 

 

Общее число элементов в системе в этом случае переменно

 

 

Нормирующее соотношение остается, конечно, в силе.

В качестве примера рассмотрим цех, оборудованный большим числом N однотипных станков. На каждый из них действует поток неисправностей с интенсивностью , не зависящий от числа неисправных станков. Ремонтом станков занимается бригада рабочих. Ее производительность , выраженная числом станков, восстанавливаемых в единицу времени, также постоянна. Каждый станок может находиться в одном из двух состояний: ₁ - исправен, ₂- ремонтируется. Граф состояний станка показан на рис. 8.1. Средняя интенсивность потока ремонтов в расчете на один станок /X₂. В соответствии с принципом квазирегулярности ее следует положить равной /m₂. Уравнения динамики средних численностей исправных и ремонтируемых станков имеют вид

 

 

При начальных условиях: t = 0, m₁=N, m₂=0 решением системы будет

 

Рис. 8.1.

 

В стационарном режиме математическое ожидание и дисперсия числа исправных станков в соответствии с (8,1) равны

 

 

8.2. Модель высоко организованного боя

Так называется модель боя, который ведется по следующим правилам [6]:

1) стрельба противниками ведется только по непораженным целям; перенос огня на новую цель производится мгновенно;

2) одним выстрелом может быть поражена только одна цель;

3) огонь равномерно распределен по всем непораженным целям.

Рассматриваем две противоборствующие группировки А и В. Каждая из них состоит из однотипных боевых единиц (БЕ) числом N_a и N_b соответственно. БЕ группировок могут находится только в двух состояниях либо в боеспособном ( _a1,  _b1), либо нет ( _a2,  _b2). Графы состояний БЕ изображены на рис. 8.2. Обозначим

 

 

 

 

Рис. 8.2.

X_a1 , X_a2, X_b1, X_b2 - случайные численности БЕ;

m _a1, m _a2, m _b1, m _b2 - ответствующие математические ожидания;

s _a, s _b- скорострельности БЕ;

p _a, p _b- вероятности поражения цели на выстрел.

Интенсивность потока поражающих выстрелов группировки В,

приходящихся на одну БЕ группировки А, равна

 

(8.4)

Аналогично

Воспользуемся принципом квазирегулярности, тогда

Уравнения динамики средних, включая нормирующие соотношения, имеют вид

(8.5)

В качестве начальных условий используем:

m_a1(0) = N_a; m_b1(0) = N_b; m_a2(0) = m_b2 (0) = 0.

Дифференцируя первое уравнение системы и подставляя в него третье, найдем

где k² = s_as_bp_ap_b > 0.

Решение этого дифференциального уравнения таково

Поскольку при t>0 решение должно оставаться конечным, следует положить C₂= 0, тогда

Аналогично

 

Из полученных соотношений видно, что бой выигрывает та группировка, начальная численность которой больше, вне зависимости от скорострельности и эффективности огня. Этот заведомо неверный вывод обусловлен погрешностями принципа квазирегулярности. Его применение допустимо тогда, когда вариации случайных численностей БЕ невелики. В рассматриваемом случае это условие выполняется только в начальной стадии боя и, безусловно, не выполняется в его конце.

 

8.3. Другие модели боев

В модели боя без переноса огня в отличие от рассмотренного в предыдущем параграфе случая принимается, что информация о состоянии противника не поступает и, следовательно, огонь равномерно распределен по всем БЕ противника вне зависимости от их состояния. Поэтому вместо (8,4) следует принять для интенсивностей перехода

Уравнения динамики средних становятся нелинейными и принимают вид.

(8.6)

Нормирующие соотношения остаются без изменений.

Модели (8,5) и (8,6) - два крайних случая. Более реален случай когда перенос огня присутствует, но выполняется с задержкой. Пусть на передачу информации требуются промежутки времени _a и _b. Кроме того, перераспределение целей невозможно после производства выстрела. Обозначим времена полета снарядов _a и _b. Теперь дифференциальные уравнения динамики средних принимают вид

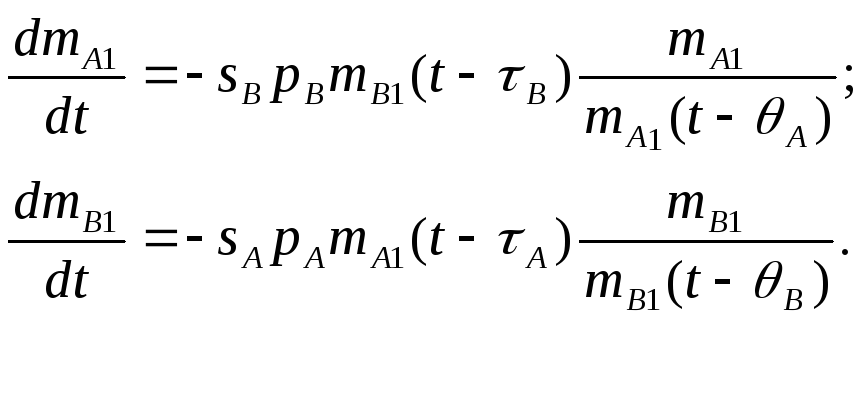
Аналитическое решение этих уравнений, вероятно, уже невозможно, но для имитационного моделирования препятствий нет.

 

Упражнения.

1. Решите методами динамики средних задачу из лабораторной работы о противоборстве танков и вертолетов. При расхождении результатов расчета с результатами лабораторной работы найдите этому объяснение.

2. Сопоставьте метод динамики средних с изложенным в п.7.3.