Глава 3 Моделирование непрерывных случайных величин

Толщина листового проката, ошибка любого измерения, стартовая масса ракеты - все это примеры непрерывных случайных величин. Их однозначное и полное определение дается законом распределения в виде функции или плотности распределения. В некоторых случаях закон распределения может быть получен теоретически (пример приведен в 6.2.), в других случаях закон распределения устанавливается экспериментально. Так на рис. 3.1 приведен полигон распределения толщины полки прессованного профиля из сплава Д16Т и выравнивающая кривая нормального закона. Данные получены автором [2] по результатам обмеров более 1000 образцов.

Рис. 3.1.

Прежде чем рассматривать моделирование непрерывных случайных величин на ЭВМ, напомним некоторые положения теории вероятностей.

3.1. Функции случайных аргументов

Рассмотрим функцию. Если аргумент функции - случайная величина, то и функция тоже величина случайная. Задача состоит в том, чтобы по известному закону распределения аргумента найти закон распределения функции.

Рассмотрим случай монотонно возрастающей функции . Рис. 3.2 иллюстрирует существо задачи и ее решение, основанное на равенстве площадей. Введем в рассмотрение функцию , обратную функции . Теперь функцию распределения случайной величины найдем при помощи следующей цепочки очевидных равенств:

Рис. 3.2.

Для определения плотности распределения f(y) необходимо определенный

интеграл в полученном выражении продифференцировать по параметру y:

Этот результат легко обобщить на случай монотонно убывающей функции:

Напомним, что для вычисления математического ожидания Y закон ее распределения определять не нужно.

3.2. Метод обращения функции распределения

Рассмотрим алгоритм генерирования непрерывной случайной величины с заданным законом распределения, основанный на материале предыдущего параграфа.

Пусть случайная величина задана плотностью распределения . Функция ее распределения . Обозначим Введем также обратную функцию . Отметим, что вероятность неравенства < x, совпадает с функцией распределения

Теперь найдем функцию распределения случайной величины Y, учитывая, что функция неубывающая (см. рис. 3.3)

Рис. 3.3.

Соответствующая плотность распределения

при 0 < y <1 и 0 при других значениях.

Итак, если случайная величина распределена с плотностью, то случайная величина распределена равновероятно в интервале (0,1). Поскольку функции и монотонны, справедливо и обратное утверждение: если случайная величина распределена равновероятно в интервале (0,1) и есть функция обратная функции распределения случайной величины , то распределена с плотностью. Действительно

Следовательно, алгоритм моделирования непрерывной случайной величины с произвольным законом распределения, для которого известна функция обратная функции распределения , состоит в следующем:

1) генерируется реализация r базовой случайной величины R, распределенной равномерно в интервале (0,1);

2) определяется реализация случайной величины X из соотношения

Рассмотрим несколько примеров.

1. Известно, что длительность нормальной работы электронной аппаратуры между двумя ремонтами имеет экспоненциальное распределение

Здесь - среднее число отказов в единицу времени. Соответствующая функция распределения

Положим , отсюда . Следовательно, генератор экспоненциально распределенной случайной величины должен использовать следующее соотношение между случайной величиной X и базовой случайной величиной R

2. Рассеивание точек падения по дальности Y и боку Z при стрельбе снарядами распределены нормально. Если средние квадратичные отклонения по дальности и боку одинаковы и равныто расстояние от центра группирования до точки падения распределен по закону Рэлея

Соответствующая функция распределения

Следовательно, генератор случайной величины, распределенной по закону Рэлея, должен использовать соотношение

соответствующая программа на Фортране может иметь вид

Subroutine Ralay (S, Ix, Iy)

call Randu(Ix, Iy, R)

X= S*sqrt(-2.0*alog(R))

return

end

3.3. Нормальное распределение

Нормально распределенные случайные величины встречаются чаще других из-за того, что случайность - это обычно проявление многих одновременно действующих причин, и, следовательно, характер закона распределения подчиняется центральной предельной теореме. Пример нормального распределения толщины проката приведен на рис 3.1.

Плотность вероятности нормального распределения описывается выражением

Здесь - математическое ожидание и среднее квадратическое отклонение случайной величины.

К сожалению, функция распределения и обратная ей функция не могут быть выражены аналитически, поэтому метод, рассмотренный в 3.2, оказывается непригодным. Задача, тем не менее, может быть решена приближенно, если использовать подходящую аппроксимацию обратной функции. Например, случайная величина

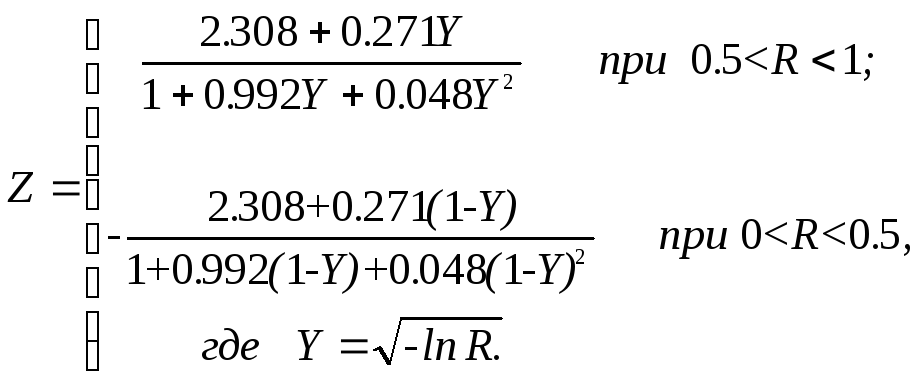
распределена приблизительно нормально с нулевым математическим ожиданием и дисперсией, равной единице. Как и раньше R равновероятна в интервале (0, 1). Следовательно, для Х имеем

Другой способ моделирования нормального распределения основан на применении центральной предельной теоремы. Если n случайных величин независимы и распределены равновероятно в интервале (0,1), то распределение случайной величины

тем ближе к нормальному, чем больше n, а математическое ожидание и дисперсия соответственно равны 0 и 1. Часто достаточно положить n=12, тогда Соответствующая программа на Фортране имеет вид.

Subroutine Gauss(Ix, S, E, X)

A=0.0

do i = 1, 12

call Randu(Ix, Iy, R)

A= A + R

end do

X = E + S*(A - 6.0)

return

end

Входные параметры подпрограммы E и S - математическое ожидание и среднее квадратическое отклонение случайной величины X.

Этот вариант имеет малую точность за пределами . Пределы могут быть расширены до , если “хвосты” распределения подкорректировать следующим образом

3.4. Метод Неймана

Метод Неймана или иначе метод исключения относится к числу

M

Да

Нет

Рис. 3.4 Рис. 3.5

универсальных, не накладывающий на моделируемый закон распределения

жестких ограничений, как, например, первый из рассмотренных. Для применения этого метода достаточно двух условий:

1) интервал (a, b) , на котором распределена случайная величина - конечен;

2) плотность распределения ограничена сверху

На плоскости (рис. 3.4) выделим прямоугольник с основанием (ab) и высотой c. Пусть точка М случайна и имеет равномерное распределение внутри этого прямоугольника. Для этого координаты точки должны быть независимы и

иметь равномерное распределение в интервалах (a,b) и (0, c). Алгоритм моделирования (см. блок-схему на рис. 3.5) состоит в следующем.

1. Генерируются две реализации базовой случайной величины .

2. Выполняются преобразования:

3. Вычисляется значение плотности вероятности моделируемого распределения

4. Выполняется сравнение Если , осуществляется возврат к п.1, иначе значение принимается в качестве реализации случайной величины X.

Несложное доказательство справедливости алгоритма состоит в следующем. Рассмотрим событие А, состоящее в том, что в одиночном испытании точка М окажется под кривой плотности распределения, т.е. Вероятность события A равна отношению площадей:

Условная вероятность события А, вычисленная при определенном значении , равна отношению отрезков: Следовательно, плотность условного распределения при условии, что точка М находится под кривой плотности распределения совпадает с плотностью моделируемого распределения:

Здесь - плотность распределения .

3.5. Точность косвенных измерений

В этом и следующем параграфе рассматриваются две имитационные модели, предполагающие использование генераторов независимых случайных величин.

Измерение физической величины - это не только оценка ее числового значения, но и определение точности полученной оценки. Результат измерения обычно представляется в виде доверительного интервала, накрывающего истинное значение с наперед заданной вероятностью. В метрологии различают прямые, косвенные, совместные и совокупные измерения. Эти виды измерений отличаются друг от друга методами их статистической обработки.

Уравнение косвенных измерений физической величины y имеет вид В этом уравнении непосредственно в опыте измеряются прямо или косвенно аргументы , искомая же величина y находится путем вычислений. Например, косвенно измеряются

- электрическая мощность W по разности потенциалов U и току I или сопротивлению R

- удельный импульс тяги ЖРД I по тяге P и расходам горючего и окислителя m_г и m_о

- коэффициент подъемной силы по подъемной силе Y, плотности воздуха , скорости полета V и характерной площади S

Для построения доверительного интервала необходим закон распределения результата измерения Y. Если законы распределения погрешностей измерения аргументов уравнения косвенного измерения известны, а сами погрешности независимы то функция распределения случайной величины Y определяется m- кратным интегралом

где область интегрирования определяется неравенством

Практически воспользоваться приведенным соотношением удается крайне редко из-за непреодолимых математических сложностей. С другой стороны закон распределения можно установить методом имитационного моделирования. Если, например, погрешности прямых измерений аргументов уравнения косвенных измерений распределены нормально, то имитация большой серии косвенных измерений объемом N, может быть осуществлена при помощи следующей программы.

dimension X(M), E(M), S(M), Y(N)

. . .

do j = 1, N

do i = 1, M

call Gauss(Ix, S(I), E(I), X(I))

Y(J) = Func(X)

end do

end do

. . .

Здесь E и S - массивы математических ожиданий ( или их оценок) и средних квадратических ошибок аргументов уравнения косвенного измерения, а Func - подпрограмма- функция, содержащая это уравнение.

Соответствие выборочных данных, содержащихся в массиве Y, некоторому теоретическому распределению проверяется при помощи критериев Пирсона или Колмогорова-Смирнова [3]. Рассмотрим вкратце второй критерий. Прежде всего высказывается гипотеза H₀ о том, что различие между эмпирической и теоретической F(y) функциями распределения вызвано только случайными причинами и альтернативную ей гипотезу H₁. Затем выборочные данные перестраиваются в вариационный ряд, то есть в упорядочный в порядке возрастанмя ряд значений Y:

и строится эмпирическая функция распределения

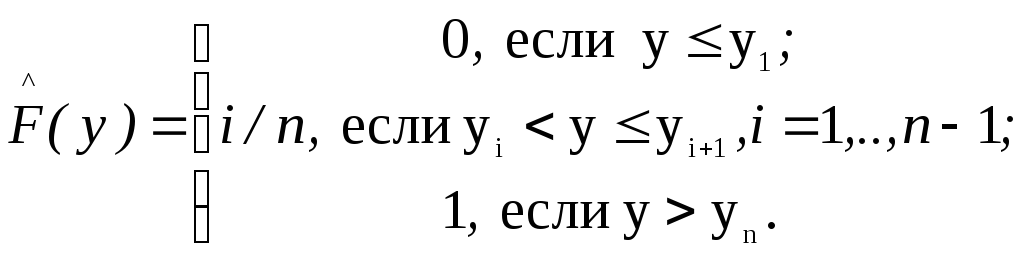
Расстояние Колмогорова между эмпирической и теоретической функциями распределения равно

Если верна гипотеза H₀ и n > 20, то случайная величина имеет распределение Колмогорова [14].

Вероятности , уровни значимости  = 1 -  и соответствующие критические значения z_кр приведены ниже.

 0.995 0.99 0.975 0.95 0.90 0.85 0.8 0.75

 0.005 0.01 0.025 0.05 0.10 0.15 0.20 0.25

z_кр 1.73 1.63 1.48 1.36 1.22 1.14 1.07 1.02

Решающее правило критерия Колмогорова:

3.6. Простая стохастическая модель баллистической ракеты

В качестве второго примера стохастической модели, содержащей ряд независимых случайных величин, рассмотрим сильно упрощенную модель одноступенчатой жидкостной баллистической ракеты. Модель предназначена для определения гарантированной дальности и гарантийных остатков топлива.

Система уравнений движения ракеты в проекциях на оси скоростной системы координат имеет вид

В этих уравнениях

m - масса ракеты;

V - скорость ее полета;

P - тяга;

X - сила лобового сопротивления;

g - ускорение свободного падения;

- угол наклона траектории к местному горизонту;

h и l - высота и дальность полета.

При постоянном во времени массовом расходе топлива масса

Угол наклона траектории изменяется по программе практически одинаковой для всех ракет:

Здесь - относительная масса израсходованного запаса топлива, изменяющаяся в пределах , где -масса рабочего запаса топлива. _к- конечное значение угла наклона траектории.

Для интегрирования уравнений движения ускорение тяги ЖРД преобразуют следующим образом

где - стартовая тяговооруженность,

- коэффициент пустотного приращения тяги;

- удельные импульсы тяги в пустоте и на земле;

- атмосферное давление на высоте h и на уровне моря.

Ускорение силы лобового сопротивления преобразуют аналогично:

,

где - коэффициент лобового сопротивления “эталонной” ракеты, имеющей “карандашную” форму и удлинение 10:1;

i - коэффициент формы ракеты;

- стартовая нагрузка на мидель ракеты;

- плотность воздуха на высоте h.

Начальными условиями при решении приведенной системы уравнений служат равенства

Как видно из изложенного траектория полета однозначно определяется следующим набором характеристик ракеты:

С другой стороны можно считать, что облик ракеты и параметры ее траектории определяют следующие независимые случайные величины:

m_г - заправленная в бак масса горючего;

m_ок - масса окислителя;

m_л - суммарная масса деталей ракеты, изготовленных из листового проката;

m_пр - суммарная масса остальных деталей;

m_т- массовый расход топлива;

k_m- соотношение между массовыми расходами топливных компонентов в полете;

- удельный импульс тяги в пустоте;

- площадь миделя;

S_а - площадь выходного сечения сопла;

- коэффициент формы ракеты;

- атмосферное давление на уровне моря;

- угол наклона вектора скорости в момент выключения двигателя.

Одна часть входящих в этот перечень величин случайна в связи с погрешностями измерений при заправке ракеты топливом (m_г, m_ок) при настройке двигателя на режим (m_т,k_m), при измерении параметров траектории в полете (). Случайность других величин обязана своим происхождением производственным погрешностям (,,,m_л,m_пр). Наконец, пустотный удельный импульс случаен в связи со случайным характером примесей в топливе.

Для того чтобы связать характеристики ракеты, определяющие траекторию полета, с перечисленными случайными величинами в модель ракеты включены следующие соотношения:

- для стартовой тяги -

- для удельного импульса на земле -

- для массового расхода горючего -

- для массового расхода окислителя -

- для времени расходования горючего -

- то же окислителя -

- для максимального времени работы двигателя -

- для рабочего запаса топлива -

- для стартовой массы ракеты -

- для относительной массы рабочего запаса топлива -

- для стартовой тяговооруженности -

- для стартовой нагрузки на мидель -

Все приведенные соотношения совместно с уравнениями движения образуют стохастическую модель одноступенчатой жидкостной баллистической ракеты. Образуем массив с 12 элементами

.

Запишем алгоритм вычисления дальности полета ракеты в подпрограмме Func. Тогда имитационное моделирование N пусков ракеты при условии полного расходования одного из компонентов топлива станет возможным по программе, аналогичной той, что приведена в предыдущем параграфе.

Для определения гарантированной дальности должна быть определена функция распределения дальности . Корень уравнения

есть гарантированная дальность, если - близкая к единице вероятность того, что любая дальность, не превышающая гарантированную, может быть достигнута при выключении двигателя по команде системы управления полетом, а не из-за нехватки какого-либо топливного компонента.

В зависимости от того известен или нет закон распределения F(l) применяются разные способы оценки гарантированной дальности.

Если известно, что закон распределения нормальный ,то эмпирические данные используются для оценки параметров распределения: математического ожидания и дисперсии

Гарантированная дальность находится из соотношения:

гдеквантиль уровня 1- распределения Стьюдента с n-1 степенями свободы. Если n > 30, то распределение Стьюдента можно заменить нормальным.

Если распределение F(l) неизвестно, то следует использовать эмпирическую функцию распределения (см. п. 3.5).

На графике рис. 3.6 это сплошная ступенчатая линия. Такая оценка функции распределения является состоятельной и несмещенной. Доверительный интервал (точнее коридор) для функции распределения строится с использованием распределения Колмогорова (см. п. 3.5), а именно с вероятностью  справедливы неравенства

где =z_кр из табл. п. 3.5. На графике рис 3.6 левая граница изображена пунктирными линиями. Она и определяет гарантированную дальность.

Рис. 3.6

Упражнения.

1. Составьте программу-генератор случайной величины, распределенной равновероятно в интервале(a, b).

2. Предложите алгоритм моделирования случайной величины, закон распределения которой задан не аналитически, а в виде гистограммы.

3. Повторите анализ п.3.1 для случаев

- монотонно убывающей функции;

- произвольной функции.

4. Эффективность генератора значений случайной величины характеризуется, в том числе и тем, сколько раз необходимо обращаться к генератору базовой случайной величины. Метод обращения функции распределения требует однократного обращения, процедура GAUSS - 12-ти кратного. Как следует модернизировать алгоритм Неймана, с тем, чтобы сделать его более “экономным”?

5. Как следует видоизменить перечень случайных величин п. 3.6, если вместо жидкостной ракеты рассматривать твердотопливную?