
Лекции по моделированию систем / лекция 5
.docМетод Неймана (метод исключения).
Этот метод заключается:
-
вызвать 2 случайных равномерно распределенных величины
 и
и
 в диапазоне [0,1].
в диапазоне [0,1].
![]()
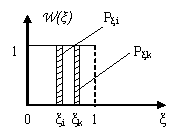 и
и
![]() - независимые равномерно распределенные
случайные величины.
- независимые равномерно распределенные
случайные величины.
![]() ,
F(x)
– интегральный
закон распределения.
,
F(x)
– интегральный
закон распределения.
Хотим получить случайную величину, которая имеет такой закон плотности вероятности ограничиваемся отрезком [a,b].
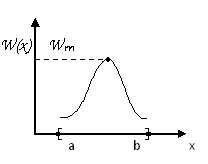
-
формируется величина
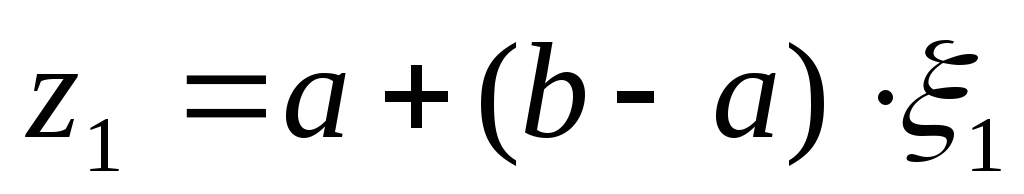 .
Это такая величина, которая появляется
между числами a
и b
с равновероятным исходом. Для данной
величины плотность вероятности будет
такова:
.
Это такая величина, которая появляется
между числами a
и b
с равновероятным исходом. Для данной
величины плотность вероятности будет
такова:
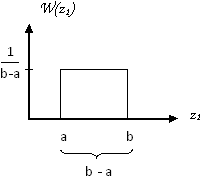
-
 .
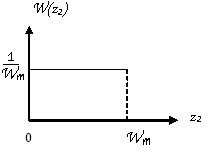
Здесь закон плотности вероятности:
.
Здесь закон плотности вероятности:
-
анализируем
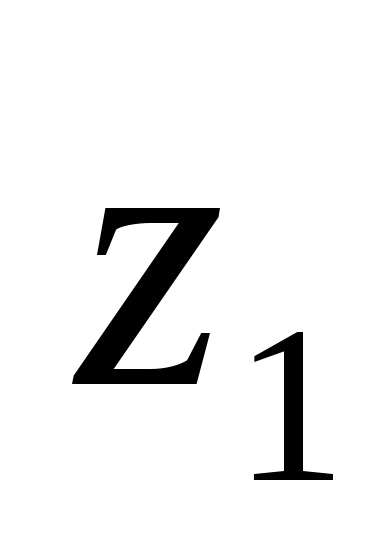 и
и
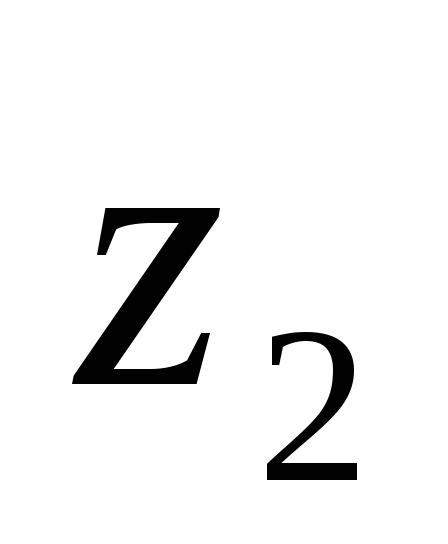 :
:
![]()
![]() переход к новой
паре
переход к новой
паре
![]() ,
,
![]() .
.
Пример: w(x) – нормальный (гауссовский) закон распределения:
 ,
,
σ – среднеквадратическое значение,
m – математическое ожидание (среднее значение).
![]()
-
Выбрать пару
Q :=
m
← 1.5 - среднее значение
:=
m
← 1.5 - среднее значение
σ ← 0.2 - СКО
N ← 1000 - число экспериментов (N +1)
a ← 1 - левый порог х
b ← 2 - правый порог х
![]() -
-
![]() (равномерно распределенное между [a,b]
число)
(равномерно распределенное между [a,b]
число)
![]() - max
w(x)
- max
w(x)
![]() -
-
![]() (равномерный на [0,
(равномерный на [0,
![]() ]
датчик)
]
датчик)
j ← -1 - индекс управляемый
for
i![]() 0..N
-
проводим (N+1)
экспериментов
0..N
-
проводим (N+1)
экспериментов

![]() - нормальный закон в точке
- нормальный закон в точке
![]()
if
(![]() )
- проверка неравенства
)
- проверка неравенства
 j
← j
+ 1 - переиндексация
j
← j
+ 1 - переиндексация
![]() - запись
- запись
![]()
![]()
Метод Неймана графически:
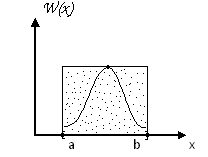
![]() - массив х
- массив х
k:=
0..![]()
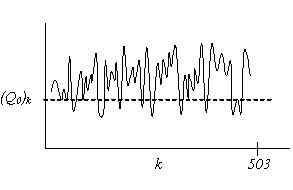
Проверка математического ожидания и СКО:
![]()
![]()
Построение гистограммы:
![]()
lower:= floor(min(x)), floor – округляет сверху
upper:= ceil(max(x)), ceil – округляет снизу
![]() - ширина интервала
суммирования.
- ширина интервала
суммирования.

j:= 0..29
![]() - ось х
(дискретная)
- ось х
(дискретная)
w:= hist(int,x)
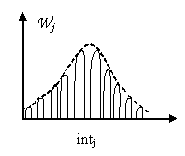
Частные методы.
-
метод формирования нормально распределенной случайной величины, использующий центральную предельную теорему теории вероятности.
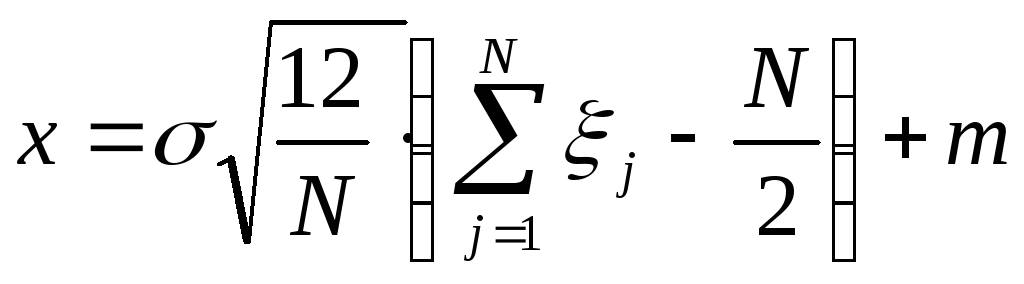 ,
,
![]()
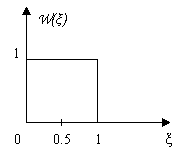
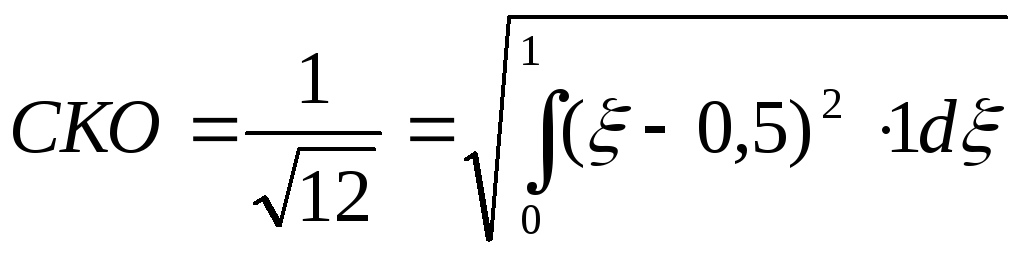
-
релеевское распределение (метод нелинейного преобразования).
![]() ,
,
![]()
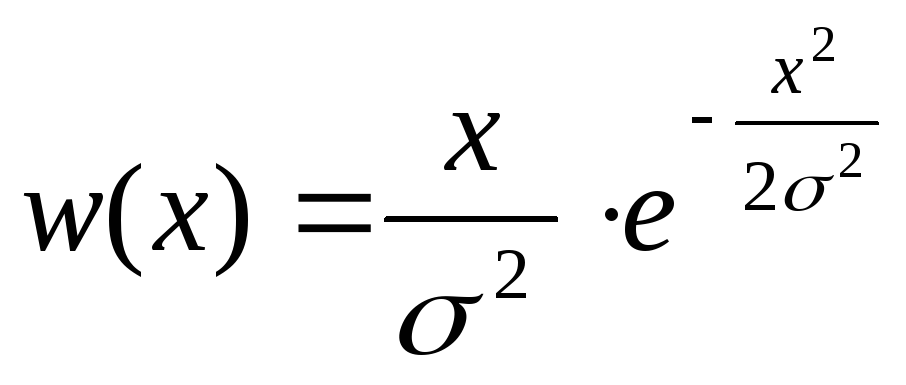
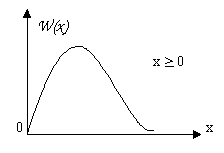
-
релеевское распределение (использование двух датчиков с нормальным).
![]() ,
,
![]() - независимое нормальное распределение.
- независимое нормальное распределение.
![]()
х – релеевское распределение.
