37.Цепь с активным сопротивлением и ёмкостью.

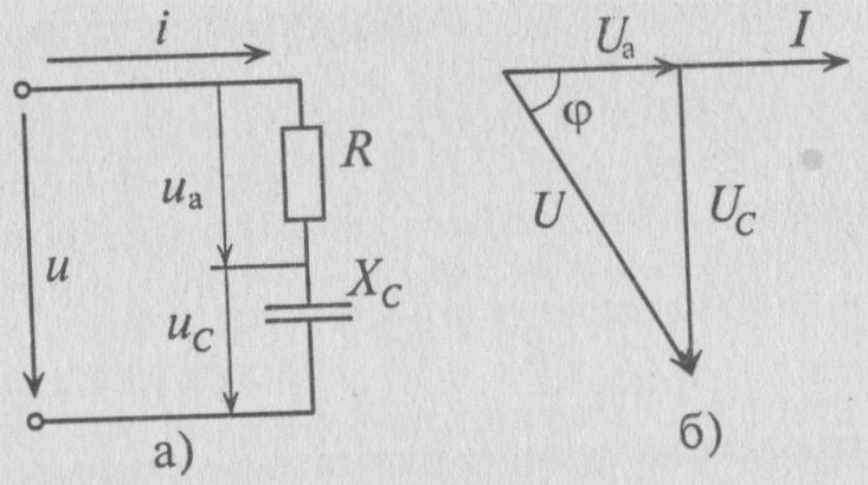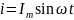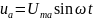Е сли в цепи с последовательно включенными активным со­противлением Rи емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении , и на емкостном сопротивлений .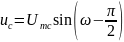

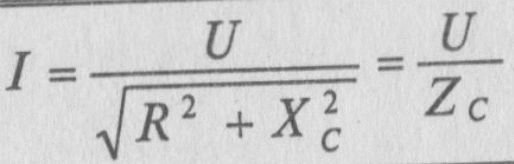
Напряжение цепи изменяется как и ток по синусоидальному закону и отстаёт по фазе от тока на угол .

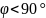38. Неразветвлённая цепь с активным сопротивлением, индуктивностью и мощностью.

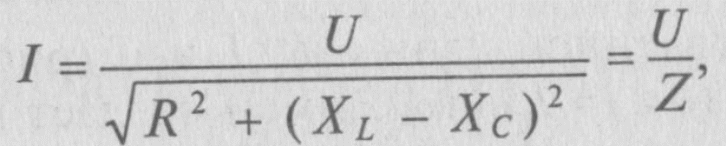
Резонанс напряжений.

Е сли в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R и индуктивностью L равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

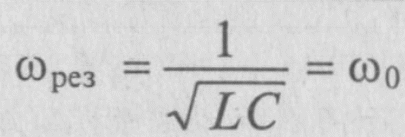
Следовательно:

Из этой формулы следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 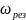будет равна частоте собственных колебаний резонансного контура ω₀. Следовательно, добиться резонанса напряжений можно изменением частоты источника или изменением параметров колебательного контура L или С, т. е. изменением частоты собственных колебаний ω₀.

Полное сопротивление цепи находится по формуле:

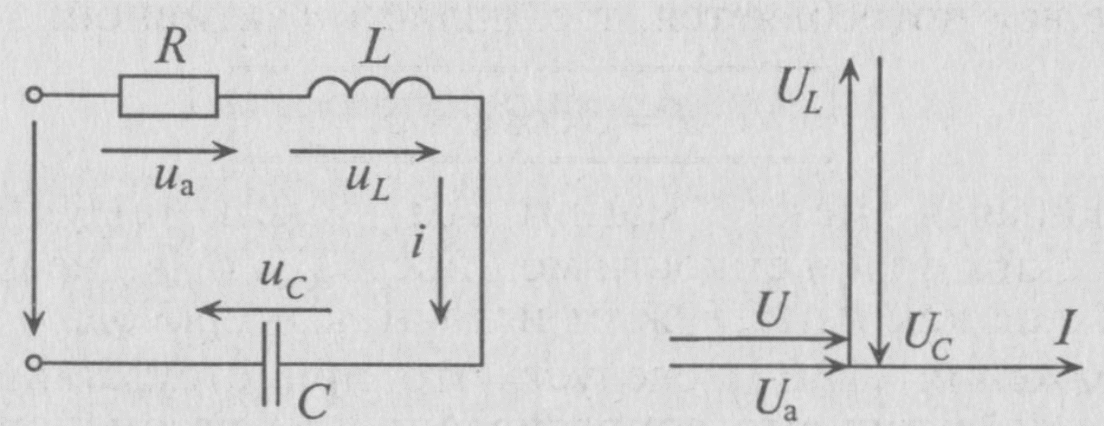
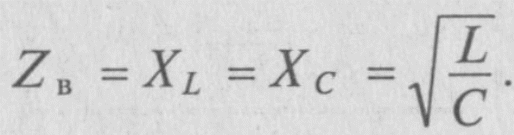
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению Z_в которое называют характеристическим сопротивлением:

Напряжения на индуктивности U_L и на емкости U_c при резонансе напряжений равны между собой, так как равны сопротивления

38. Треугольник напряжений, сопротивлений мощностей.

38. Активные и реактивные токи. Проводимости цепей.

Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.

Если к цепи, содержащей активное сопротивление R и индуктивное Х_Lприложено синусоидальное напряжение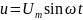 ,то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол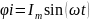

Векторные диаграммы примут вид:

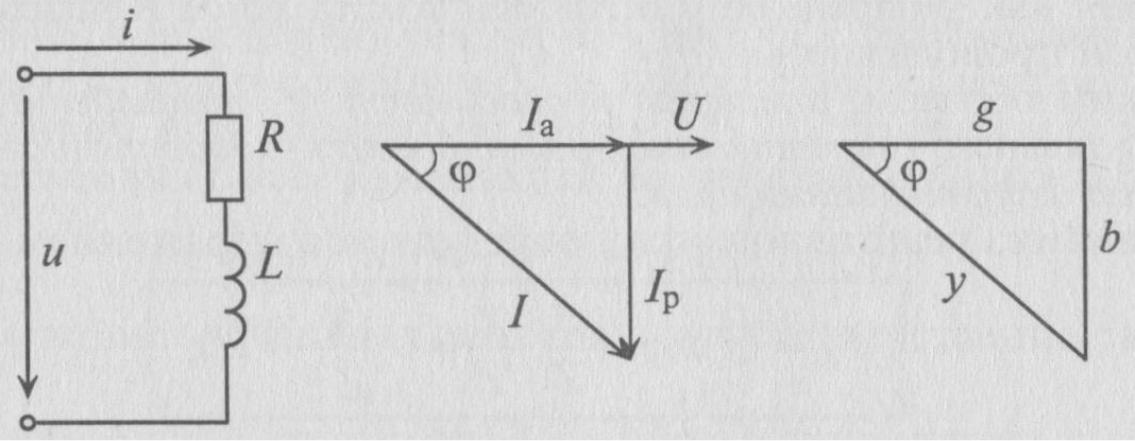
Ток цепи I раскладывается на две составляющие, одна из которых I_а совпадает по фазе с напряжением, другая I_р— сдвинута на 90°. Составляющая тока I_а, совпадающая по фазе с на­пряжением, называется активной составляющей, или активным током. Составляющая тока I_р, имеющая относительно напряже­ния сдвиг по фазе на угол 90°, называется реактивной составляю­щей, или реактивным током.

Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи ток на всех участках имеет одинаковое зна­чение. Однако понятия активный I_а и реактивный I_Ртоки значительно облегчают расчет разветвленных цепей синусоидаль­ного тока. Соотношения между токами определяются из треугольника токов.

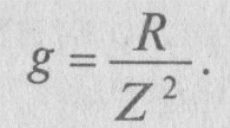
Проводимости цепей.

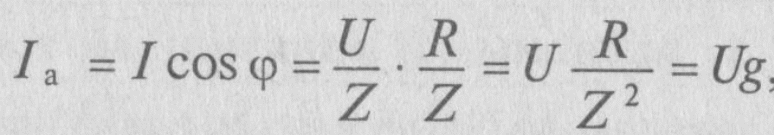
Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.

А так как g определяет активный ток I_A, то ее и называют активной проводимостью.

Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.

Величина реактивного тока определяется выражением

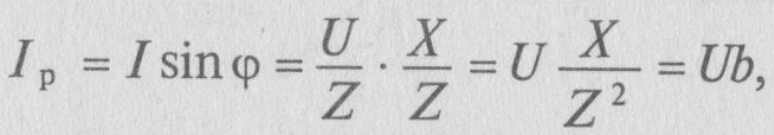
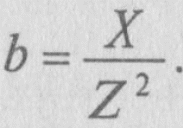
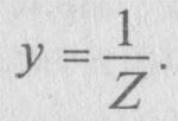-полная проводимость цепи.

41. Параллельное соединение катушки и конденсатора. Резонанс тока. Если к источнику синусоидального напряжения u=U_msinωt подключить параллельно катушку с активным сопротивлением R₁ и индуктивным X_L и конденсатор с активным сопротивлением R₂ и емкостным X_C , то действительные токи в ветвях будут соответственно равны 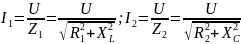. Ток в неразветвленной цепи 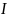будет равен: 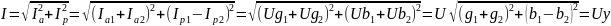, где 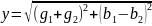-полная проводимость цепи. Реактивная проводимость со знаком минус, т.к. сопротивление в ветвях разного характера.

Резонанс токов в цепи наступает при параллельном соединении катушки и конденсатора с учетом, что b_L=b_C. Полная проводимость при этом условии 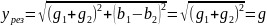. Полная проводимость в цепи минимальна по величине и равна активной, а следовательно ток в цепи будет иметь минимальную величину. Реактивные токи в ветвях при резонансе токов равны между собой 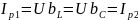. Это равенство и определяет название «резонанс токов».

42.Символический метод расчета эл. цепей переменного тока. Он основан на использовании комплексных чисел. Комплексное числоА состоит из вещественной А’ и мнимой А‘‘ частей, т.е. А=А’+jА’’, где j-поворотный множитель.

Существует 3 формы записи комплексного числа:

1. Алгебраическая: А=А’+jА’’

2. Тригонометрическая: А=IАIcosϕ+jIАIsinϕ, где IАI= , ϕ=arctg

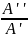
3. Показательная: А=IАIe^jϕ

Комплексные числа можно складывать, вычитать, умножать и делить. Сложение и вычитание производится только в алгебраической форме. Умножение и деление производится в показательной форме.

Ток, напряжение и сопротивление в комплексном виде: ; .

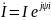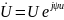Пусть комплекс тока 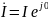, комплекс напряжения 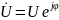. Определим комплекс сопротивления Z= .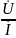

Z=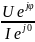 = =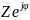Zcosϕ+jZsinϕ=R+jX; Z=R+jX.

Мощность в комплексном виде:

Пусть комплекс тока 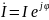, а комплекс напряжения 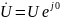, тогда комплекс мощности S=I*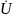 , где I*-сопряженный комплекс тока.

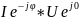S= =S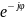 =Scos(-ϕ)+jSsin(-ϕ)=P-jQ.