5. Процессы размножения и гибели.

Процессы размножения и гибели являются частным случаем марковских случайных процессов, которые тем не менее находят весьма широкое применение при исследовании дискретных систем со стохастическим характером функционирования. Процесс размножения и гибели представляет собой марковский случайный процесс, в котором переходы из состояния E_iдопустимы только в соседние состоянияE_i-1,E_iиE_i+1. Процесс размножения и гибели является адекватной моделью для описания изменений, происходящих в объеме биологических популяций. Следуя этой модели, говорят, что процесс находится в состоянииE_i, если объем популяции равенiчленам. При это переход из состоянияE_iв состояниеE_i+1соответствует рождению, а переход изE_iвE_i-1- гибели, предполагая, что объем популяции может изменяться не более чем на единицу; это означает, что для процессов размножения и гибели не допускаются многократные одновременные рождения и/или гибели.

Дискретные процессы размножения и гибели менее интересны, чем непрерывные, поэтому в дальнейшем они подробно не рассматриваются и основное внимание уделяется непрерывным процессам. Однако следует отметить, что для дискретных процессов проходят почти параллельные выкладки. Переход процесса размножения и гибели из состояния E_iобратно в состояниеE_iпредставляет непосредственный интерес только для дискретных цепей Маркова; в непрерывном случае интенсивность, с которой процесс возвращается в текущее состояние, равна бесконечности, и эта бесконечность была исключена согласно определению (13).

В случае процесса размножения и гибели с дискретным временем вероятности переходов между состояниями

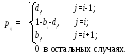
Здесь d_i- вероятность того, что на следующем шаге (в терминах биологической популяции) произойдет одна гибель, уменьшающая объем популяции доi-1 при условии, что на данном шаге объем популяции равенi. Аналогично,b_i- вероятность рождения на следующем шаге, приводящего к увеличению объема популяции доi+1; 1-d_i-b_iпредставляет собой вероятность того, что ни одно из этих событий не произойдет и на следующем шаге объем популяции не изменится. Допускаются только эти три возможности. Ясно, чтоd₀=0, так как гибель не может наступить, если некому погибать.

Однако в противовес интуиции допускается, что b₀>0, что соответствует возможности рождения, когда в популяции нет ни одного члена. Хотя это можно расценивать как спонтанное рождение или божественное творение, но в теории дискретных систем такая модель представляет собой вполне осмысленное допущение. А именно, модель такова: популяция представляет собой поток требований, находящихся в системе, гибель означает уход требования из системы, а рождение соответствует поступлению в систему нового требования. Ясно, что в такой модели вполне возможно поступление нового требования (рождение) в свободную систему. Матрица вероятностей переходов для общего процесса размножения и гибели имеет следующий вид:

Т=

Если цепь Маркова является конечной, то последняя строка матрицы записывается в виде [0 0… 0d_n1-d_n]; это соответствует тому, что не допускаются никакие размножения после того, как популяция достигает максимального объемаn.

Матрица Tсодержит нулевые члены только на главной и двух ближайших к ней диагоналях. Из-за такого частного вида матрицыTестественно ожидать, что анализ процесса размножения и гибели не должен вызывать трудностей.

Далее будем рассматривать только непрерывные процессы размножения и гибели, в которых переходы из состояния E_iвозможны только в соседние состоянияE_i-1 (гибель) иE_i+1(рождение). Обозначим через_iинтенсивность размножения; она описывает скорость, с которой происходит размножение в популяции объемаi. Аналогично, через_iобозначим интенсивность гибели, задающую скорость с которой происходит гибель в популяции объемаi. Заметим, что введенные интенсивности размножения и гибели не зависят от времени, а зависят только от состоянияE_i, следовательно, получаем непрерывную однородную цепь Маркова типа размножения и гибели. Эти специальные обозначения введены потому, что они непосредственно приводят к обозначениям, принятым в теории дискретных систем. В зависимости от ранее введенных обозначений имеем:

_i= q_i,i+1и_i= q_i,i-1.

Требование о допустимости переходов только в ближайшие соседние состояния означает, что исходя из (14), q_ii=-(_i+_i). Таким образом, матрица интенсивностей переходов общего однородного процесса размножения и гибели принимает вид

Q

.

=

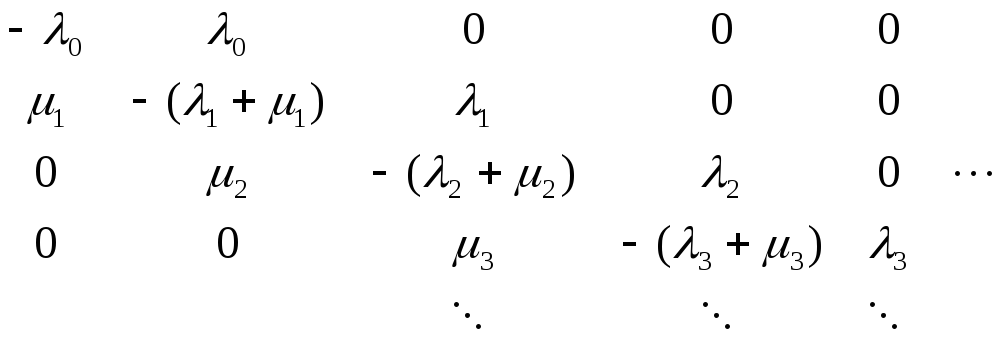
Заметим, что за исключением главной и соседних с ней снизу и сверху диагоналей все элементы матрицы равны нулю. Соответствующий граф интенсивностей переходов представлен на рис. 4.

Более точное определение непрерывного процесса размножения и гибели состоит в следующем: некоторый процесс представляет собой процесс размножения и гибели, если он является однородной цепью Маркова с множеством состояний {E₀,E₁,E₂, …}, если рождение и гибель являются независимыми событиями (это вытекает непосредственно из марковского свойства) и если выполняют следующие условия:

1. Pr[точно 1 рождение в промежутке времени (t,t+Δt)| объем популяции равенi]= ;

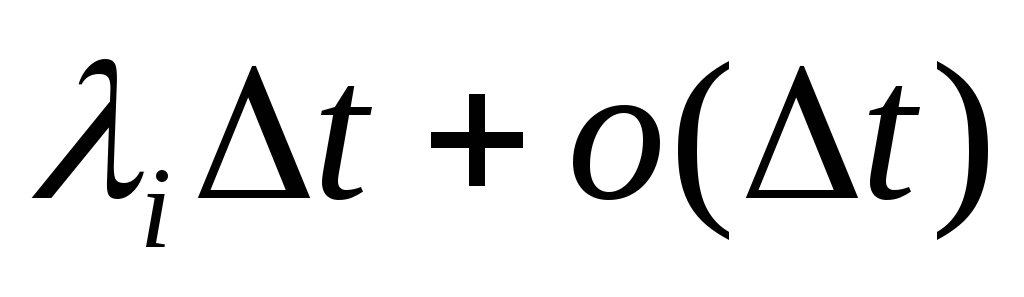2. Pr[точно 1 гибель в промежутке времени (t,t+Δt)| объем популяции равенi]= ;

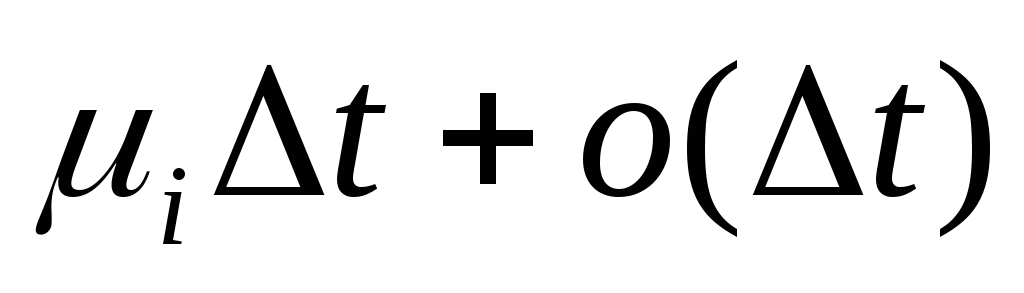3. Pr[точно 0 рождений в промежутке времени (t,t+Δt)| объем популяции равенi]= ;

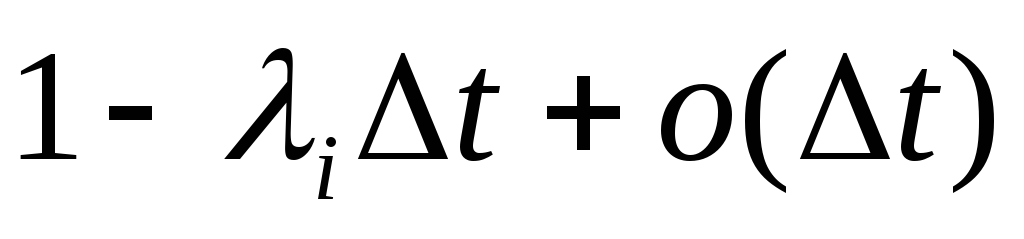4. Pr[точно 0 гибелей в промежутке времени (t,t+Δt)| объем популяции равенi]= .

Согласно этим предположениям кратные рождения, кратные гибели и одновременные рождения и гибели в течение малого промежутка времени (t,t+Δt) запрещены в том смысле, что вероятность таких кратких событий имеет порядоко(Δt).

Вероятность того, что непрерывный процесс размножения и гибели в момент времени tнаходится в состоянииE_i(объем популяции равенi) определяется напрямую из (16) в виде

(18)

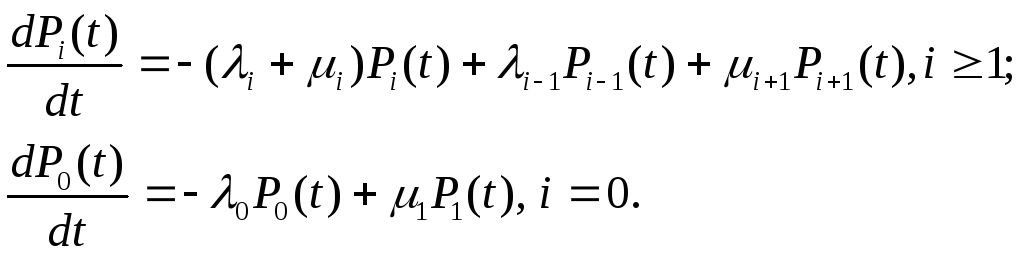
Для решения полученной системы дифференциальных уравнений в нестационарном случае, когда вероятности P_i(t),i=0,1,2,…, зависят от времени, необходимо задать распределение начальных вероятностейP_i(0),i=0,1,2,…, приt=0. Кроме того, должно удовлетворяться нормировочное условие.

Рис.4. Граф интенсивностей переходов для процесса размножения и гибели.

Рассмотрим теперь простейший процесс чистого размножения, который определяется как процесс, для которого _i= 0 при всехi. Кроме того, для еще большего упрощения задачи предположим, что_i=для всехi=0,1,2,... . Подставляя эти значения в уравнения (18) получим

(19)

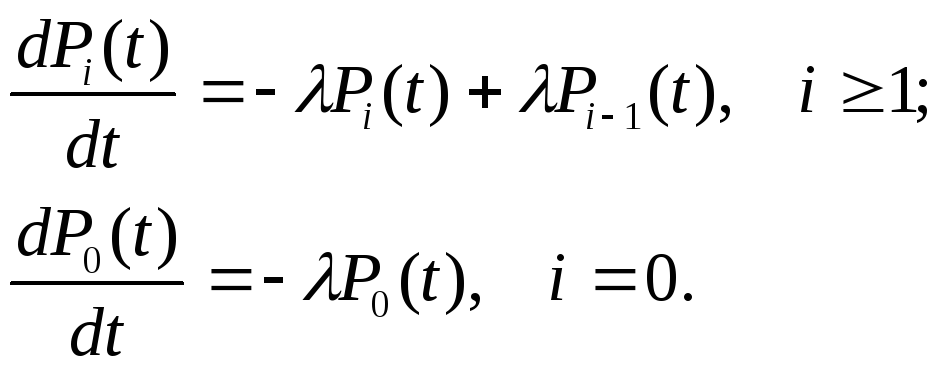
Для простоты предположим также, что процесс начинается в нулевой момент при нуле членов, то есть:

(20)

Отсюда для P₀(t) получаем решение

P₀(t)=e^-t.

Подставляя это решение в уравнение (19) при i= 1, приходим к уравнению

.

Решение этого дифференциального уравнения, очевидно, имеет вид

P₁(t)= te^-t.

Далее по индукции в качестве решения уравнения (19) находим

.

Это знакомое нам распределение Пуассона. Таким образом, процесс чистого размножения с постоянной интенсивностью приводит к последовательности рождений, образующей пуассоновский процесс.

Наибольший интерес в практическом плане представляют вероятности состояний процесса размножения и гибели в установившемся режиме. Предполагая, что процесс обладает эргодическим свойством, т.е. существуют пределы перейдем к определению предельных вероятностейP_i.

Уравнения для определения вероятностей стационарного режима можно получить непосредственно из (18), учитывая, что dP_i(t)/dt= 0 при :

(21)

Полученная система уравнений решается с учетом нормировочного условия

(22)

Систему уравнений (21) для установившегося режима процесса размножения и гибели можно составить непосредственно по графу интенсивностей переходов на рис.4, применяя принцип равенства потоков вероятностей к отдельным состоянием процесса. Например, если рассмотреть состояние E_iв установившемся режиме, то:

интенсивность потока вероятностей в и

интенсивность потока вероятностей из .

В состоянии равновесия эти два потока должны быть равны, и поэтому непосредственно получаем

Но это как раз и есть первое равенство в системе (21). Аналогично можно получить и второе равенство системы. Те же самые рассуждения о сохранении потока, которые были приведены ранее, могут быть применены к потоку вероятностей через любую замкнутую границу. Например, вместо того, чтобы выделять каждое состояние и составлять для него уравнение, можно выбрать последовательность контуров, первый из которых охватывает состояние E₀, второй - состояниеE₀иE₁, и т.д., включая каждый раз в новую границу очередное состояние. Тогда дляi-го контура (окружающего состоянияE₀,E₁, ...,E_i-1) условие сохранения потока вероятностей можно записать в следующем простом виде:

(23)

.

Полученная система уравнений эквивалентна выведенной ранее. Для составления последней системы уравнений нужно провести вертикальную линию, разделяющую соседние состояния, и приравнять потоки через образовавшуюся границу.

Решение системы (23) можно найти методом математической индукции.

При i=1 имеем:

при i=2:

при i=3:

и т.д.

Вид полученных равенств показывает, что общее решение системы уравнений (23) имеет вид

или, учитывая, что, по определению, произведение по пустому множеству равно единице

Таким образом, все вероятности P_iдля установившегося режима выражаются через единственную неизвестную константуP₀. Равенство (22) дает дополнительное условие, позволяющее определитьP₀. Тогда, суммируя по всемi, дляP₀получим:

Обратимся к вопросу о существовании стационарных вероятностей P_i. Для того, чтобы полученные выражения задавали вероятности, обычно накладывается требование, чтобыP₀> 0. Это, очевидно, налагает ограничение на коэффициенты размножения и гибели в соответствующих уравнениях. По существу требуется, чтобы система иногда опустошалась; это условие стабильности представляется весьма резонным, если обратиться к примерам реальной жизни. Определим следующие две суммы:

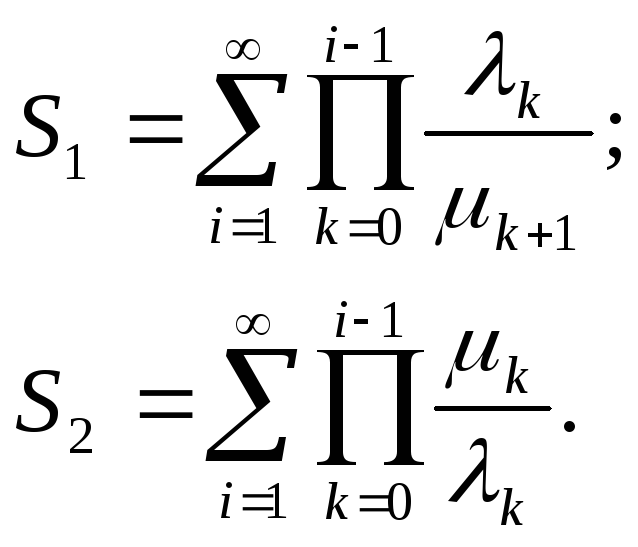
Все состояния E_iрассматриваемого процесса размножения и гибели будут эргодическими тогда и только тогда, когдаS₁<иS₂=. Только эргодический случай приводит к установившимся вероятностямP_i,i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются только тогда, когда, начиная с некоторогоi, все члены последовательности {} ограничены единицей, т.е. тогда, когда существует некотороеi₀(и некотороеС<1) такое, что для всехii₀выполняется неравенство:

1Символo(t) ("o" малое отt) означает произвольную функцию, которая приt0,стремится к нулю быстрее, чемt, т.е..

14