4. Марковские процессы с непрерывным временем.

Для марковских процессов с непрерывным временем, когда переходы из одного состояния в другое возможны в любой момент времени, вероятность перехода из состояния E_i в состояние E_j точно в момент времени t не может быть задана, поскольку такая вероятность равна нулю. Вместо этого можно определить вероятность соответствующего перехода на интервале времени (t, t+t), определяемая как

p_ij (t, t +t)=Pr {g (t+t)=E_j | g (t)=E_i}, i, j=0,n.

При этом,i,j=0,n.

В случае марковской цепи с непрерывным временем для описания переходов используются не вероятности переходов, а интенсивности переходов. Интенсивность перехода из состоянияE_iв состояниеE_jв момент времениt, обозначаемая черезq_ij(t), определяется следующим образом:

q_ij(t)=, ij; (12)

q_ii(t)=. (13)

Эти пределы имеют следующую интерпретацию. Если в момент времени tпроцесс находится в состоянииE_i, то вероятность перехода в течение промежутка времени (t,t+t) в произвольное (отличное отE_i) состояние задается величиной -q_ii(t)t+o(t)¹. Таким образом, величину -q_ii(t) можно интерпретировать как интенсивность, с которой процесс уходит из состоянияE_i. Аналогично, вероятность перехода процесса в течение времени (t,t+t) из состоянияE_iв состояниеE_jзадается величиной +q_ij(t)t+o(t) и величинуq_ij(t) можно интерпретировать как интенсивность, с которой процесс переходит из состоянияE_iв состояниеE_j, при условии, чтоE_i- текущее состояние процесса. Так как всегда(t,t+t)=1, то из равенств (12) и (13) следует, что

(14)

(t)=0,i=0,n.

Если вероятности переходов p_ij(t,t+t), а, значит, и интенсивности переходовq_ij(t), не зависят от времениt (p_ij(t,t+t)p_ij(t) иq_ij(t)q_ij), т.е. от того, в какой момент начинается промежутокt, то марковский процесс называетсяоднородным, в противном случае -неоднородным.

Далее, рассматривая марковские случайные процессы с непрерывным временем, будем считать их однородными.

Интенсивности переходовq_ij, i,j=0,n, можно задать в виде квадратной матрицыQразмерности (n+1)(n+1):

называемая матрицей интенсивностей переходов. Элементы матрицы переходов Qудовлетворяют условию (14) (сумма элементов строки равна нулю), и такая матрица называется дифференциальной.

Рассмотрим теперь задачу определения вероятностей (2) марковского случайного процесса с непрерывным временем.

Вероятность того, что марковский процесс в момент времени t+tокажется в состоянииE_i, определяется как

P

(15)

_i(t+t) = (t)p_ji(t), i=0,n.

Действительно, марковский процесс в момент времени t+tокажется в состоянииE_i, если он в момент времениtнаходится в состоянииE_j(с вероятностьюP_j(t)) и за промежуток времениtперейдет с вероятностьюp_ji(t) из состоянияE_jв состояниеE_i. Суммируя произведения вероятностей этих двух независимых событий по всем возможным состояниям процесса в момент времениt, получим равенство (15).

Если вычесть P_i(t) от обоих сторон равенства (15), а затем разделить наtи определить соответствующие пределы приt0, то получим:

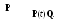,i=0,n

или в векторном виде: (16)

Решая данную систему дифференциальных уравнений при заданном распределенииP(0)={P₀(0),P₁(0), ...,P_n(0)} начальных вероятностей с учетом нормировочного условия (3), можно определить вероятностиP_i(t),i=0,n,состояний марковского случайного процесса в любой момент времени.

Вслучае эргодичности марковского случайного процесса существуют предельные (приt) вероятности состоянийP_i,i=0,n,и они не зависят от начальных условий и временного параметра. Тогда производныеdP_i(t)/dt=0,i=0,n, и система дифференциальных уравнений (16) для стационарного режима превращается в систему линейных алгебраических уравнений:

,i=0,n

или в векторном виде (17)

PQ=0.

Система (17) совместно с нормировочным условием дает единственное решение для стационарных вероятностейP_i,i=0,n.

Систему уравнений для вероятностей состояний равновесия марковского процесса с непрерывным временем можно составить непосредственно по графу переходов, используя принцип равенства потоков вероятностей, который состоит в следующем: в состоянии равновесия марковского процесса поток вероятностей в любое состояние равен потоку вероятностей из этого состояния. При этом под потоком вероятностей, например, в данное состояние, понимается сумма произведений интенсивностей переходов в это состояние на вероятности тех состояний, откуда происходят эти переходы. Принцип равенства применим не только к потоку вероятностей для отдельных состояний, но и к потоку через любую замкнутую границу.

Пример. Определим вероятности состояний равновесия марковского случайного процесса с четырьмя возможными состояниямиE₀, E₁, E₂, E₃и матрицей интенсивностей переходов

Г

λ

λ

раф переходов для этого процесса приведен на рис. 3. В диаграмму переходов не включены петли, ведущие из состоянияE_i,i=0,3, обратно в это же состояние, так как, согласно (14), члены на главной диагонали матрицыQ не содержат никакой новой информации: они равны сумме элементов соответствующей строки, взятой со знаком минус.

λ

P₀

P₁

P₂

P₃

μ

μ

μ

Рис. 3. Граф переходов примера.

Система (17) вместе с нормировочным условием для этого примера имеет вид:

-P₀+P₁=0

P₀-(+)P₁+P₂=0

-(+)P₂+P₃=0

P₁+P₂-P₃=0

P₀+P₁+P₂+P₃=1

Первые четыре уравнения полученной системы являются линейно зависимыми, и любое из них можно исключить из системы, а остальные три уравнения и нормировочное условие определяют единственное решение для вероятностей состояний равновесия. Если  = 2 и = 1, тоP₀=1/19,P₁=2/19,P₂=4/19 иP₃=12/19.

Применение принципа равенства потоков вероятностей к отдельным состояниям дает такую же систему уравнений. Так, например, для состояния E₃P₁+P₂=P₃, что соответствует четвертому уравнению приведенной выше системы.