- •Дифференциальные уравнения
- •Образцы решения заданий
- •2. Найти общее решение уравнения и частное решение, удовлетворяющее начальным условиям .
- •Варианты контрольных заданий
- •В задачах 291 – 300 найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
- •Контрольная работа № 8
- •В задачах 321 – 330 исследовать на сходимость ряд.
Варианты контрольных заданий
КОНТРОЛЬНАЯ РАБОТА № 7
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В задачах 271 – 280 найти общее решение дифференциального уравнения первого порядка.
271.
![]() .
272.
.
272.
![]() .
.
273.
![]() .
274.
.
274.
![]() .
.
275.
![]() .
276.
.
276.
![]() .
.
277.
![]() .
278.
.
278.
![]() .
.
279.
![]() .
280.
.
280.
![]() .
.
В задачах 281 – 290 найти общее решение дифференциального уравнения второго порядка.
281.
![]() .
282.
.
282.
![]() .
.
283.
![]() .
284.
.
284.
![]() .
.
285.
![]() .
286.
.
286.
![]() .
.
287.
![]() .
288.
.
288.
![]() .
.
289.
![]() .
290.
.
290.
![]() .
.
В задачах 291 – 300 найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
291.
![]()
292.
![]()
293.
![]()
294.
![]()
295.
![]()
296.
![]()
297.
![]()
298.
![]()
299.
![]()
300.
![]()
301. Тяжелое тело без начальной скорости
скользит по наклонной плоскости. Найти
путь, пройденный телом за время
![]() ,
если угол наклона равен
,
если угол наклона равен
![]() ,
а коэффициент трения равен
,
а коэффициент трения равен
![]() .
.
302. Найти зависимость давления воздуха
![]() от высоты
от высоты
![]() ,
если известно, что это давление равно
1
,
если известно, что это давление равно
1
![]() на 1
на 1
![]() на уровне моря
на уровне моря
![]() и 0,92
на 1
на высоте 500
и 0,92
на 1
на высоте 500
![]() .
.
303. Материальная точка массы
![]() 2
2![]() без начальной скорости медленно
погружается в жидкость. Найти путь,
пройденный точкой за время
без начальной скорости медленно
погружается в жидкость. Найти путь,
пройденный точкой за время
![]() 1
1![]() ,
считая, что при медленном погружении
сила сопротивления жидкости пропорциональна
скорости погружения (коэффициент
пропорциональности
,
считая, что при медленном погружении
сила сопротивления жидкости пропорциональна
скорости погружения (коэффициент
пропорциональности
![]() 2).
2).
304. В резервуаре находится 100
![]() раствора, содержащего 10
раствора, содержащего 10
![]() растворенной соли. В резервуар втекает
вода со скоростью 3
растворенной соли. В резервуар втекает
вода со скоростью 3
![]() ,
а смесь вытекает со скоростью 2,5
,
причем концентрация поддерживается
равномерной путем перемешивания. Сколько
соли останется в резервуаре по истечении
часа.
,
а смесь вытекает со скоростью 2,5
,
причем концентрация поддерживается
равномерной путем перемешивания. Сколько
соли останется в резервуаре по истечении
часа.
305. Катер движется в спокойной воде со
скоростью
![]() .
На полном ходу его двигатель был выключен,
и через 2
.
На полном ходу его двигатель был выключен,
и через 2
![]() скорость катера уменьшилась до
скорость катера уменьшилась до
![]() .
Определить скорость, с которой двигался
катер через 40
после выключения двигателя, считая
сопротивление воды пропорционально
скорости движения катера.
.
Определить скорость, с которой двигался
катер через 40
после выключения двигателя, считая
сопротивление воды пропорционально
скорости движения катера.
306. Найти уравнение кривой, если длина
отрезка касательной от точки касания
до пересечения ее с осью
![]() имеет постоянную длину
имеет постоянную длину
![]() .
.
307. Найти уравнение кривой, проходящей
через точку
![]() и обладающей тем свойством, что отрезок
любой ее касательной, заключенный между
осями координат, делится в точке касания
в отношении 2:3, считая от оси ординат.
и обладающей тем свойством, что отрезок
любой ее касательной, заключенный между
осями координат, делится в точке касания
в отношении 2:3, считая от оси ординат.
308. Найти уравнение кривой, радиус кривизны которой равен постоянной величине
309. Найти уравнение кривой, проходящей
через точку
![]() и обладающей тем свойством, что касательная
к ней в точке с координатами
и обладающей тем свойством, что касательная
к ней в точке с координатами
![]() проходит через точку с координатами
проходит через точку с координатами
![]() .
.
310. Найти уравнение кривой, проходящей
через точку
![]() и обладающей тем свойством, что касательная
к ней в любой точке пересекает прямую
в точке, ордината которой в три раза
больше ординаты точки касания.
и обладающей тем свойством, что касательная
к ней в любой точке пересекает прямую
в точке, ордината которой в три раза
больше ординаты точки касания.
В задачах 311 – 320 найти общее решение системы дифференциальных уравнений.
311.
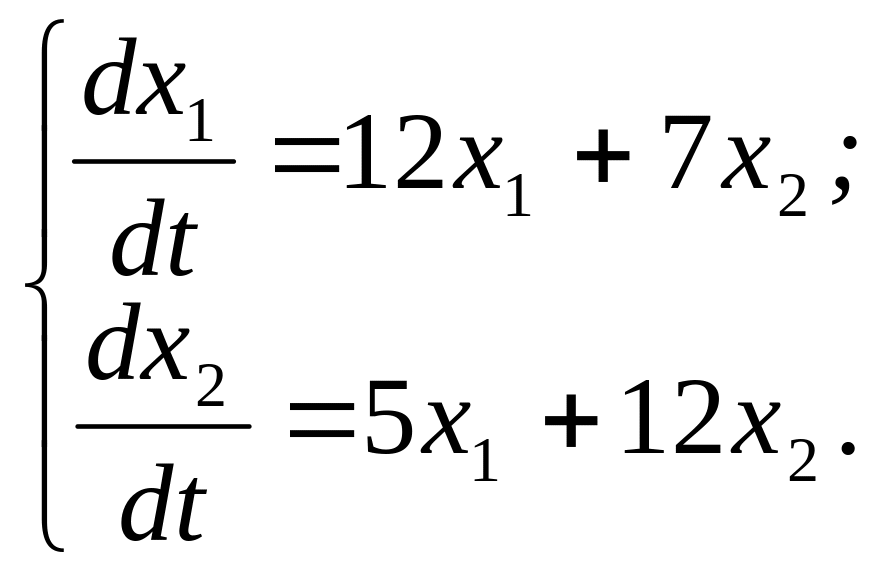 312.
312.
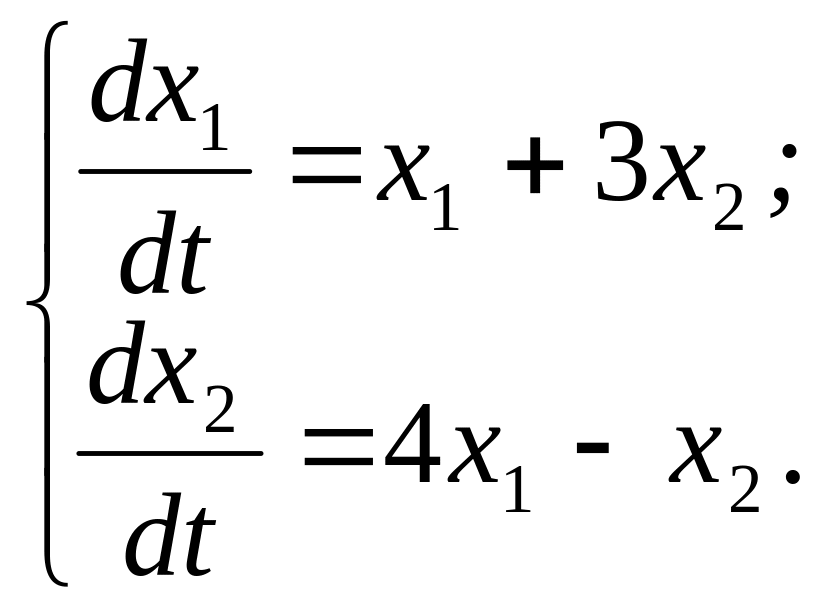
313.
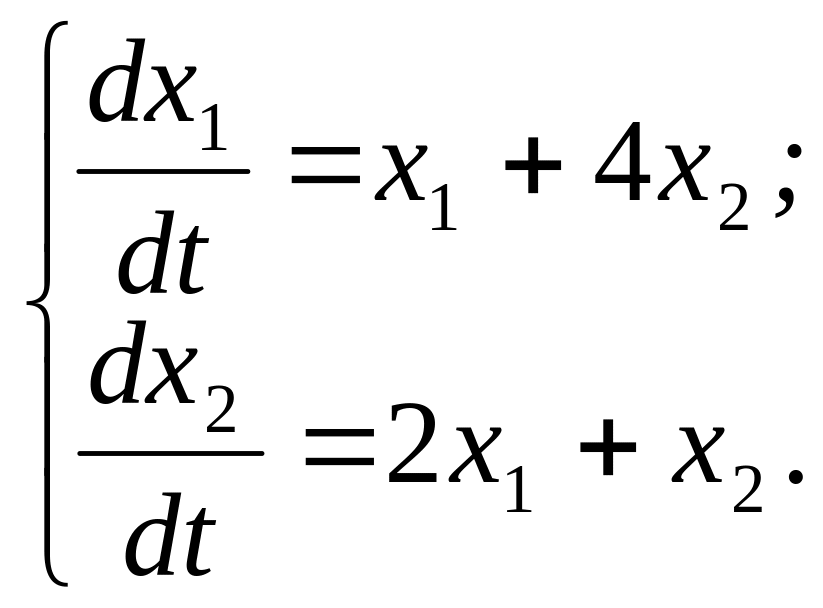 314.
314.
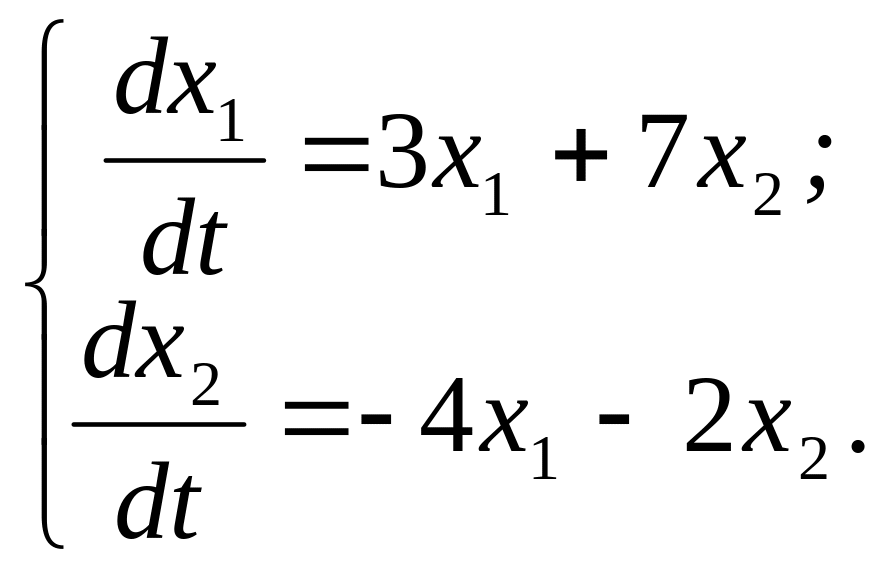
315.
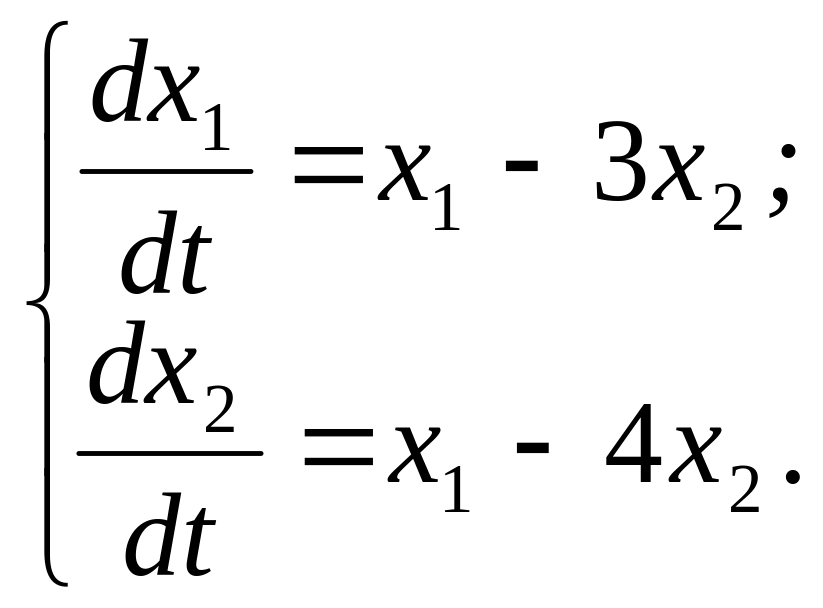 316.
316.
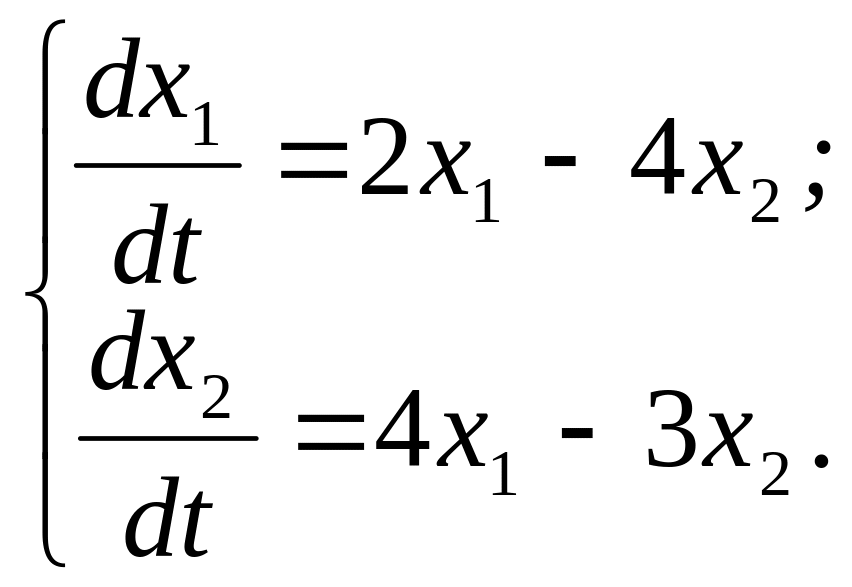
317.
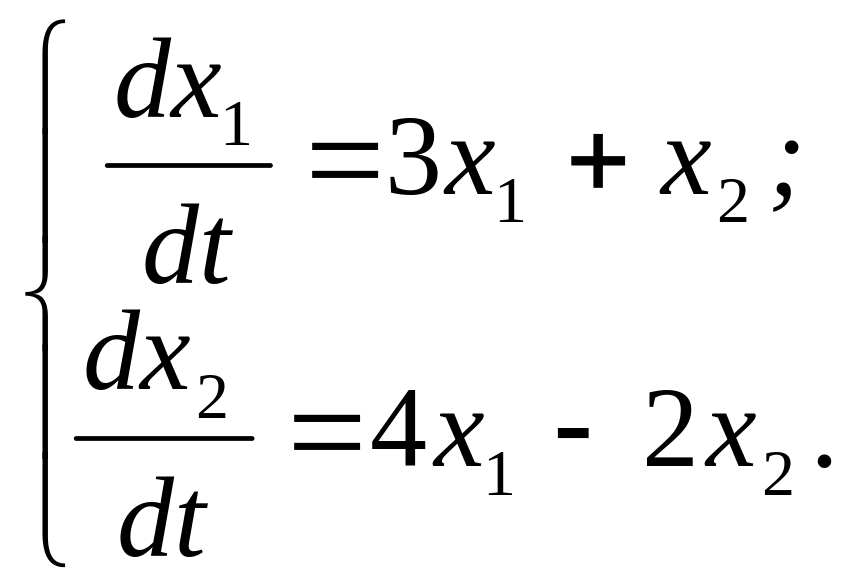 318.
318.
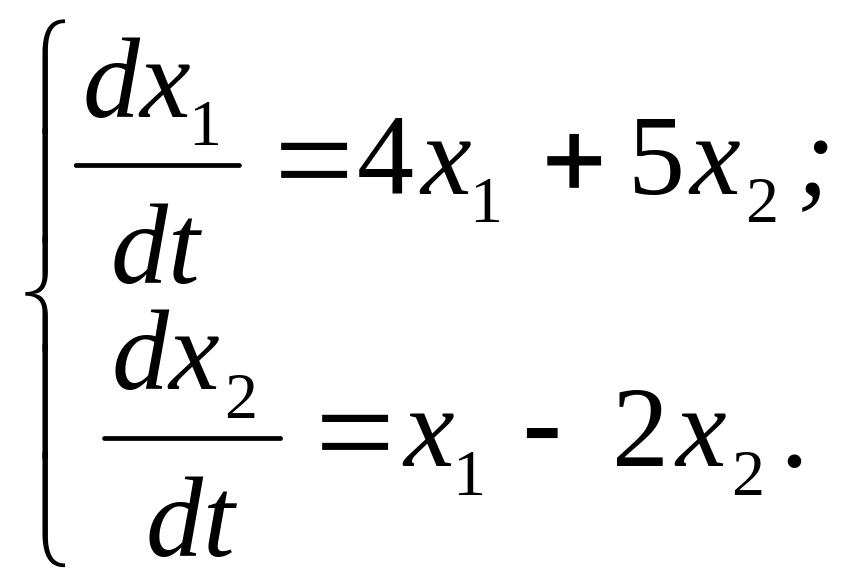
319.
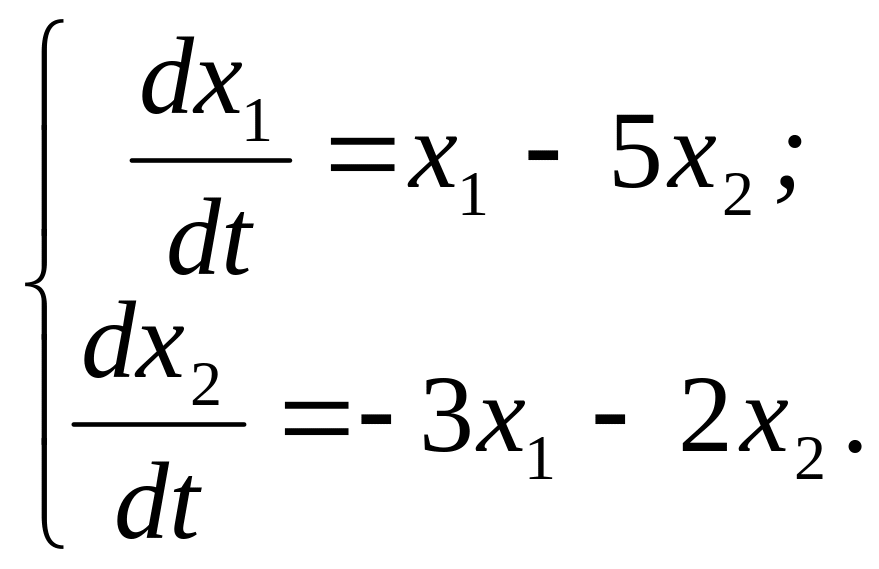 320.
320.