Содержание

Формулировка задачи

Метод решения задачи

Описание программ для расчётов

Результаты расчётов с таблицами и графиками

Выводы

Список используемых источников

Формулировка задачи

Построить контур в комплексной плоскости ζ и рассчитать распределение коэффициентов давления, а также коэффициенты аэродинамических сил и момента действующих на контур. Контур С в плоскости ζ получается с помощью отображения окружности в плоскости z с помощью функции конформного отображения

Etta=1/2*(z+r0^2/z). Окружность в плоскости Z имеет радиус R=1, и смещена относительно начала координат на d=0.1*r и f=0.1*r по оси x и y соответственно. Хорда контура в плоскости ζ b=1,5 м.

Углы атаки alpha=0,10,20 градусов. Течение плоское, среда невязкая, несжимаемая, Обтекание контура С установившееся и безотрывное.

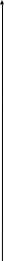y

R

O1

f

O

d

x

Метод решения задачи

1. Построение контура.

Для того чтобы построить контур дана функция ζ=1/2(z+r0^2/z)

ζ=1/2*(z+r0^2/z), и параметры окружности в плоскости z. Однако в функции ζ неизвестной величиной является r0. Для того чтобы ее вычислить надо воспользоваться условием, что хорда контура b=1.5м.

В плоскости Z окружность делится осью Ox на 2 части. Та часть которая находится выше оси Оx отобразится в верхнюю поверхность контура C, а та часть которая находится ниже оси Ох отобразится соответственно в нижнюю поверхность контура С. Из уравнения окружности найдем точки, которые принадлежат окружности, и в которых y=0. пусть эти точки будут z1 и z2.

При помощи функции ζ эти точки отобразятся на плоскость ζ и будут иметь новые координаты ζ1 и ζ2. Так как ζ1=ξ1+i0, ζ2=ξ2+i0, получаем b=|ξ1-ξ2|, а так как z1=x1+i0,z2=x2+i0

и ζ=1/2*(z-r0^2/z) получим b*2=(x1+r0^2/x1)-(x2+r0^2/x2) выражая из этого уравнения r0 получим

r0^2=(2*b-x1+x2)/(1/x1-1/x2), (x1>x2).

r0=0.7052699

Зная значение R0 с помощью функции ζ строится контур С. Верхняя и нижняя часть окружности делятся на 180 точек, и каждая такая точка Z отображается в точку ζ. В результате мы имеем точки верхней и нижней поверхности контура С. Значения Re(ζ) и Im(ζ) для верхней и нижней поверхности приведены в табл.1, контур С изображен на Рис.1

2 Вычисление циркуляции Г.

Несмотря на то что контур С не имеет острых углов, чтобы точкой торможения была передняя точка контура необходимо чтобы выполнялось условие dw/dz |_{z=zпередн или задн} =0.Для этого запишем характеристическую функцию W(z) и найдем ее производную.

W(z)=6.79

dw/dz=-v*e^(i*alpha)*(1-(e^-2ialpha)/z^2)+Г/2/3.14/i/z.

откуда Г= v*e^(i*alpha)*(1-e^(-2ialpha)/z^2)*2*3.14*z

Передней точке контура C соответствует z=x1+i0, задней точке контура С соответствует z=x2+i0

Подставляя координаты этих точек в dw/dz вычисляется циркуляция Г. Значения циркуляций Г в зависимости от углов атаки приведены в табл.2

3 Нахождение поля скоростей.

Чтобы найти скорость на верхней и нижней поверхности контура С необходимо знать Dw/dz и функцию ζ. Обе эти функции известны, так как dw/dζ=dw/dz*dz/dζ получаем

dw/dζ=dw/dz/f'(z) где dζ/dz=f'(z).

f'(z)=1/2*(1-r0^2/z)

dw/dζ=u-i*v. так как вдоль линий тока нормальная составляющая скорости равна нулю, получаем что модуль касательной скорости |Vт|=Sqrt(u^2+v^2).

Значения Vт приведены в табл.3 для различных углов атаки

4 Нахождение Ср.

Так среда несжимаемая и известна касательная скорость, наиболее просто Ср вычислить с помощью формулы

Ср=1-v^2/Uбеск^2. Uбеск=2*Vбеск

Значения приведены в табл.4, зависимости отображены на рис.2, рис.3, рис.4

если распределение давления по контуру профиля известно, то главный вектор аэродинамических сил и главный момент вычисляются по формулам

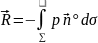
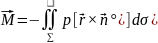
Полагая, что контур профили задан уравнениями

y1н=fн(x1); y1в=fв(x1)

(индексы "н" - нижняя часть, "в"-верхняя) в связанной системе координат, и, вводя коэффициент давления и коэффициенты сил и момента, после несложных преобразований

Cy=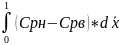

Cx=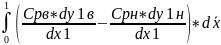

Mz=

между коэффициентами аэродинамических сил в связанной и скоростной системах координат имеет место связь

Cya=Cy*cos(alpha)-Cx*sin(alpha)

Cxa=Cx*cos(alpha)+Cy*sin(alpha)

Значения и зависимости приведены в табл.5, и рис 5,6,7.