Свойства дифференциала. Инвариантность формы дифференциала

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

 (С – постоянная величина)  (8)

                                (9)                              (10)

                                      (11)

                            (12)

Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на  .

Рассмотрим дифференциал сложной функции. Пусть  - сложная функция  :

Дифференциал

этой функции, используя формулу для производной сложной функции, можно записать в виде

Но   есть дифференциал функции  , поэтому

,

т.е.

                                      (13)

Здесь дифференциал записан в том же виде, как и в формуле (7), хотя аргумент  является не независимой переменной, а функцией  . Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называютинвариантностью (неизменностью) формы дифференциала.

Подчеркнём, что в формуле (13) нельзя заменить  на  , так как

для любой функции  , кроме линейной.

51Производные основных элементарных функций

Билет 52. Производная обратной и сложной функций.

Производная сложной функции.

Пусть - функция, дифференцируемая в точке , - функция, дифференцируемая в точке , причем . Тогда - сложная функция независимого переменного , дифференцируема в точке и ее производная в этой точке вычисляется по формуле .

Обычно называют внешней функцией, а - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке определена дифференцируемая функция , которую называют обратной к , а ее производная вычисляется по формуле

.

53 Вопрос. Логарифмическая производная. Производная функции u(X)V(X).

Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции:

Используя формулу производной сложной функции, найдем, что .Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.

Вывод формулы логарифмической производной. Для примера найдем производную показательно степенной функции x в степени x. Логарифмирование дает . По свойствам логарифма . Дифференцирование обеих частей равенства приводит к результату: 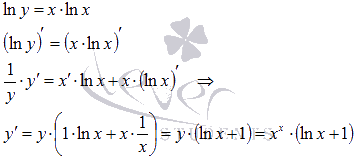Ответ: .

При дифференцировании показательно степенной функции или громоздких дробных выражений удобно пользоваться логарифмической производной.

Билет 54. Основные теоремы дифференциального исчисления.

Теорема Ролля, теорема о корнях производных.

Доказательство:

Пусть гладкая на , .

Тогда :

Любая гладкая функция, имеющая на концах отрезка одинаковые значения имеет, внутри этого отрезка, хотя бы один корень производной.

при

при

Билет 55. Экстремум функции одной переменной.

Говорят, что в точке x₀ функция имеет максимум, если для любых точек взятых из окрестности точки x₀ выполняется неравенство f(x)<f(x₀) x(x₀-, x₀+ f(x)<f(x₀) в точке х₀ достигается максимум. F (x)=0 – стационарные точки.

Пусть x₀ – критическая точка.

Если при переходе через точку х₀ у  меняет знак с «+» на «-», то х₀-максимум, наоборот – минимум.

+ (a, x₀) y >0 f(x) – возрастает.

– (x₀, d) y <0 f(x) – убывает.