Формула конечных приращений

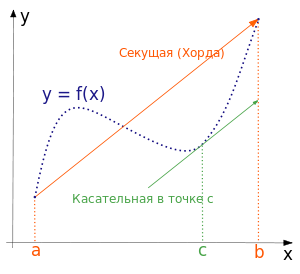
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция  непрерывна на отрезке   и дифференцируема в интервале  , то найдётся такая точка  , что

.

Геометрически это можно переформулировать так: на отрезке   найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть   — расстояние точки в момент   от начального положения. Тогда   есть путь, пройденный с момента   до момента  , отношение   — средняя скорость за этот промежуток.

Для функции одной переменной:

Введем функцию  . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны  . Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции   равна нулю:

Правила дифференцирования функций

Если скалярные величины u и v дифференцируемы, то:

а)  ;

б)  ;

в)  ;

г)  ;

Если вектор-функции u и v дифференцируемы, то

а) d(u ± v) = du ± dv;

б) d(u, v) = (du, v) + (u, dv);

в) d(λu) = udλ + λdu (λ - скалярная функция).

Если u и v - скалярные дифференцируемые функции, то

d(u ± iv) = du ± i dv,     i² = -1.

Если A, B - дифференцируемые матричные функции, u - дифференцируемая вектор-функция, то

а) d(A ± B) = dA ± dB;

б) d(Au) = (dA)u + A du;

в) d(AB) = (dA)B + A dB.

Инвариантность формы и геометрический смысл первого дифференциала

Понятие дифференциала

Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следовательно, в точке xсуществует конечная производная

Тогда по определению предела функции разность

                            (1)

является бесконечно малой величиной при  . Выразив из равенства (1) приращение функции, получим

                    (2)

(величина   не зависит от  , т. е. остаётся постоянной при  ).

Если  , то в правой части равенства (2) первое слагаемое  линейно относительно  . Поэтому при

оно является бесконечно малой того же порядка малости, что и  . Второе слагаемое  - бесконечно малая более высокого порядка малости, чем первое, так как их отношение   стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно  частью приращения функции; чем меньше  , тем большую долю приращения составляет эта часть. Поэтому при малых значениях  (и при  ) приращение функции можно приближенно заменить его главной частью  , т.е.

                (3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

или

Следовательно,

                   (4)

или

             (5)

Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (5) это видно из записи, в формуле (4) – нет.

Дифференциал функции можно записать в другой форме:

                      (6) или

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении xна величину  .