Геометрический смысл предела числовой последовательности

Число a – предел последовательности x_n, если в любую окрестность числа а, начиная с некоторого номера попадают все члены последовательности  .

 

Пример 17.4.

Показать, что последовательность   не имеет предела. Действительно, пусть а – предел x_n..

Выберем интервал   с длиной  . Расстояние между -1 и 1  равно 2 и, следовательно, они оба не могут попадать в этот интервал.

 

Основные свойства сходящихся последовательностей

 

Теорема 17.2.

Если последовательность {x_n} имеет предел, то он единственный.

 

Доказательство

Пусть {x_n} имеет два предела a и b. Накроем их интервалами(c,d) и  (e,f) (т.е.  ) Т.к. a=lim x_n , то все элементы {x_n} начиная с некоторого номера лежат в (c,d)  и значит это противоречит тому, что b – предел.

 

Теорема 17.3.

Если последовательность {x_n} сходится, то она ограничена.

 

Доказательство

Пусть  . Зададим  . Тогда  :  .

Известно, что                                    ,

 

поэтому <1

.

Пусть  ,

тогда очевидно, что  .

Арифметические действия над последовательностями, имеющими предел

Замечание 1.

Пусть  , тогда   - бесконечно малая последовательность.

Действительно,  .

Это значит, что любой элемент последовательности {x_n}, имеющей пределом число  , можно представить в виде:

 (17.1).

 

Замечание 2.

Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Замечание 3.

Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Замечание 4.

Так как  , то  .

 

Теорема 17.4.

Если существуют конечные пределы последовательностей   и  , то справедливы равенства:

1)       (17.2)

2)         (17.3)        

3) 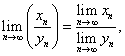  если   (17.4).

 

Доказательство

Идея доказательства построена на неравенстве:

.

Пусть  ,  . Тогда согласно равенству (17.1):

1)  - бесконечно малая последовательность (согласно 17.1);

2)   (бесконечно малая последовательность);

3) 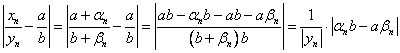  (бесконечно малая последовательность).

 

Предел функции на бесконечности

Понятие предела функции на бесконечности является в определенном смысле обобщением понятия предела последовательности, поэтому настоящий пара­граф мы построим по аналогии с параграфом о пределе последовательности.

1. Бесконечно малые функции при х

Рассмотрим на луче [1, + ] функции f(x)=1/х и g(х) = — 2/х². Их графики обладают общей особенностью: неограниченно (в математике говорят «асим­птотически») приближаются к положительному направлению оси х. Ось х называется горизонтальной асимптотой графика той и другой функции. Такие функции называют бесконечно малыми при x . Более строгое определе­ние почти дословно повторяет определение бесконечно малой последова­тельности.

Определение 1. Функцию  (х), определенную на некотором луче [Q,+  ), называют бесконечно малой при х , если для любого   > 0 существует число  М>0 такое, что при всех х>М вы­полняется неравенство |  (х)| < в. Короче:

( >0)( M>0)( )|  (x)|<  .

Свойства бесконечно малых при х  функций аналогичны свойствам бесконечно малых последовательностей.

Теорема 1. Постоянная функция у=с является бесконечно малой при х  тогда и только тогда, когда с=0.

Теорема 2. Если  (х) — бесконечно малая функция при х  и для всех х из некоторого луча [Q,+  ),  выполняется неравенство | (x)| |  (x)|, то и  (х) есть бесконечно малая функция при х  .

Теорема 3. Если  (х) — бесконечно малая функция при x , то она является ограниченной на некотором луче [М, + ).

Эти теоремы мы приводим без доказательств, так как они легко следуют из определения 1.

Теорема 4. Сумма двух бесконечно малых при х  функций также является бесконечно малой при х  функцией.

Теорема 5. Если  (х) — бесконечно малая при х  функция, а у=f(х) — ограниченная функция на некотором луче [а, + ), то их произведение является бесконечно малой при х   функцией.

Следствие 1. Если  (х) — бесконечно малая при х  функция, то и с (х), где с — любое действительное число, также является бесконечно малой при х  функцией.

Следствие 2. Произведение двух (и вообще любого конечного числа) бесконечно малых при х  функций есть бесконечно малая при х  функция.

Следствие 3. Если  ₁(х),  ₂(х), ...,  _n(х)—бесконечно малые при х   функции, то и c_{1 1}(х) + c_{2 2}(х) + ••• + c_{n n}(x) (где С₁, ..., С_n — действительные числа) также является бесконечно малой при х  функцией.

Например, функция у=  есть бесконечно малая при x .