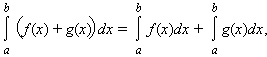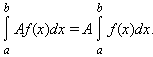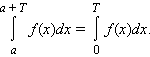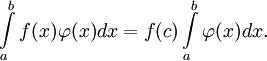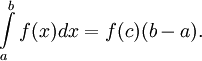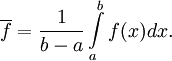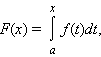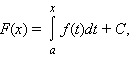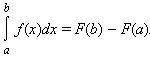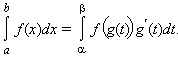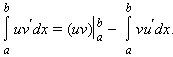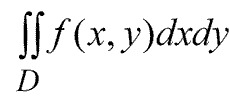- •9. Вырожденные и невырожденные матрицы. Ранг матрицы. Теорема о ранге матрицы.
- •Уравнение плоскости по трем точкам:
- •4. Уравнение плоскости по точке и двум неколлинеарным векторам
- •Геометрический смысл предела числовой последовательности
- •Основные свойства сходящихся последовательностей
- •Арифметические действия над последовательностями, имеющими предел
- •1. Бесконечно малые функции при х
- •2. Предел функции при х и его свойства.
- •1. Бесконечно малые функции при х а
- •2. Предел функции в точке
- •3. Односторонние пределы
- •44 Вопрос. Глобальные свойства непрерывных функций.
- •Формула конечных приращений
- •Понятие дифференциала
- •Свойства дифференциала. Инвариантность формы дифференциала
- •51Производные основных элементарных функций
- •53 Вопрос. Логарифмическая производная. Производная функции u(X)V(X).
- •56 Вопрос. Направление вогнутости. Точки перегиба.
- •64 Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.
- •66 Экстремум функции нескольких переменных
- •Билет 70. Неопределенный интеграл. Простейшие свойства.
- •Для неопределённого интеграла
- •Для определённого
- •Метод замены переменной (метод подстановки)
- •72Интегрирование дробно-рациональных функций
Билет 70. Неопределенный интеграл. Простейшие свойства.
![]()
![]() Совокупность
всех первообразных функции f (x)
на промежутке D
называют неопределенным
интегралом
функции f (x)
и обозначают символом :
Совокупность
всех первообразных функции f (x)
на промежутке D
называют неопределенным
интегралом
функции f (x)
и обозначают символом :
![]()
(знак ∫ – модифицированная буква S в латинском слове Summa – сумма).
Неопределенный интеграл обладает свойством линейности: интеграл от линейной комбинации функций равен линейной комбинации от интегралов этих функций.
Основные свойства
1.
![]()
![]()
2.
![]()
![]()
![]() 3. Если
то
3. Если
то
![]()
4.
71. Интегрирование подстановкой и по частям.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы формулы
для
неопределённого
интеграла:![]()
для
определённого:![]()
Предполагается,
что нахождение интеграла
![]() проще,
чем
проще,
чем
![]() .
В противном случае применение метода
не оправдано.
.
В противном случае применение метода
не оправдано.
Для неопределённого интеграла
Функции
![]() и
и
![]() гладкие,
следовательно, возможно дифференцирование:
гладкие,
следовательно, возможно дифференцирование:![]()
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
![]()
Операция
интегрирования обратна
дифференцированию:![]()
После перестановок:
Для определённого
В целом аналогично случаю неопределённого интеграла:
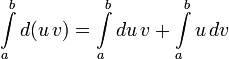 ,
,
Метод замены переменной (метод подстановки)
Метод
интегрирования подстановкой заключается
во введении новой переменной интегрирования
(то есть подстановки). При этом заданный
интеграл приводится к новому интегралу,
который является табличным
или к нему сводящимся. Общих методов
подбора подстановок не существует.
Умение правильно определить подстановку
приобретается практикой.Пусть требуется
вычислить интеграл
![]() .
Сделаем подстановку
.
Сделаем подстановку
![]() ,
где
,
где
![]() —
функция, имеющая непрерывную
производную.Тогда
—
функция, имеющая непрерывную
производную.Тогда
![]() и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
![]()
72Интегрирование дробно-рациональных функций
Пусть ![]() и
и ![]() некоторые
полиномы степени m и n
некоторые
полиномы степени m и n
![]()
![]()
Функция вида
![]()
называется дробно-рациональной функцией , или коротко-рациональной дробью.
При m<n эта рациональная дробь называется правильной.
Интегралы от дрбно –рациональных функций всегда вычисляются. Однако в данном курсе мы не будем рассматривать полную теорию интегрирования таких функций , а рассмотрим только два наиболее важных частных случая
Случай 1 Подинтегральная функция имеет вид
![]() ,
,
где
все ![]() различны
и m<n , т.е. рациональная дробь
является правильной .
различны
и m<n , т.е. рациональная дробь
является правильной .
Основной результат который мы приведём без доказательства , утверждает , что f(x) в этом случае можно представить в виде:
![]()
Слагаемые
вида ![]() называются
простейшими , а само приведённое
разложение называется “разложением
рациональной дроби на простейшие”.
называются
простейшими , а само приведённое
разложение называется “разложением
рациональной дроби на простейшие”.
Рассмотрим
вопрос о нахождении коэффициентов ![]() .
Рассмотрим , например , вычисления
.
Рассмотрим , например , вычисления ![]() .
Для этого
.
Для этого
а)
Умножим обе части разложения на простейшие
на ![]()
![]()
б) И положим x=b1 . Так как при этом (x-b1)=0 , то получи
![]()
(символ ![]() означает
, что в написанном слева выражении надо
положить
означает
, что в написанном слева выражении надо
положить ![]() )
)
Аналогично можно найти и все остальные . Этот метод получил название “метода вычёркивания “. Он формулируется так : чтобы вычислить коэффициент нужно
а) в
выражении для f(x) вычеркнуть сомножитель ![]()
б) в
оставшемся выражении положить ![]() .
.
Если
все ![]() найдены
, то дальнейшее очень просто
найдены
, то дальнейшее очень просто
![]() и
получившиеся интегралы 1 типа легко
вычисляются
и
получившиеся интегралы 1 типа легко
вычисляются
Случай 2.
Подинтегральная функция имеет вид
![]()
![]() т.е.
сомножитель вида
т.е.
сомножитель вида ![]() даёт
группу слагаемых вида
даёт
группу слагаемых вида
![]()
Если теперь найти все коэффициенты Bi j , то метод разложения приведёт к интегралам 1 и 2 типов которые легко вычисляются.
Для нахождения коэффициентов Bi j можно использовать так называемый метод неопределённых коэффициентов .
Его алгоритм следующий.
а) пишут разложение рациональной дроби на простейшие с неопределёнными коэффициентами ;
б) написанное разложение на простейшие приводят к общему знаменателю и вновь сворачивают в правильную рациональную дробь ;
в) приравнивают коэффициенты при одинаковых степенях y x в числителях исходной дроби и получившейся дроби ;
г) решают полученную систему линейных уравнений и определяют Bi j .
Продемонстрируем этот метод на примере .
Комбинированный метод
Метод
неопределённых коэффициентов достаточно
трудоёмок .Однако заметим что коэффициенты
при старших степенях ![]() ,
т.е. при
,
т.е. при ![]() можно
определять методом вычёркивания.
можно
определять методом вычёркивания.
Поэтому реально комбинируют оба этих метода :коэффициенты при определяют метдом вычёркивания , а оставшиеся – методом неопределённых коэффициентов.
Случай 3. Подынтегральная функция имеет вид
![]() ,
,
где ![]() - неразложимые трёхчлены
. Разложение этой функции на простейшие
имеет вид.
- неразложимые трёхчлены
. Разложение этой функции на простейшие
имеет вид.
![]()
![]()
т.е.
от сомножителя ![]() идёт
слагаемое вида
идёт
слагаемое вида ![]() .
Оно при интегрировании даст интеграл
третьего типа.
.
Оно при интегрировании даст интеграл
третьего типа.
Коэффициенты
при старших степенях ![]() ,
т.е. при
,
т.е. при ![]() находятся
методом вычёркивания , остальные –
методом неопределённых коэффициентов.
находятся
методом вычёркивания , остальные –
методом неопределённых коэффициентов.
В заключение отметим , что есть рациональная дробь неправильная , т. е. Степень полинома , стоящего в числителе , выше степени полинома, стоящего в знаменателе , то следует поделить эти полиномы друг на друга, выделить целую часть и затем интегрировать отдельно полученную целую часть и оставшуюся правильную рациональную дробь.
73Интегрирование тригонометрических функций |
1.Интегралы
вида
2.Интегралы
вида Например,
3.Интегралы вида , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:
4.Интегралы
5.Интегралы
вида
Следует заметить, что использование универсальной подстановки нередко приводит к громоздким выкладкам. |
§5. Интегрирование простейших иррациональностей |
Рассмотрим методы интегрирования простейших видов иррациональностей. 1.
2.
74Интегрирование иррациональных функций Д Билет 75. Определенный интеграл. Простейшие свойства.
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала). Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
-
Если функция интегрируема на [ a ;
b ], то она интегрируема на любом отрезке
- Интеграл обладает свойством линейности: для любых функций f ( x ) и g ( x ) и любой постоянной A
- Если f ( x ) и g ( x ) интегрируемы на [ a ; b ], то f ( x ) · g ( x ) также интегрируема на этом отрезке. - Если f ( x ) – периодическая функция с периодом T , то для любого a
Билет 76. Теорема о среднем значении функции.
Среднее значение
функции — это некоторое число,
заключённое между наименьшим и
наибольшим её значениями. В
дифференциальном и интегральном
исчислении имеется ряд «теорем о
среднем», устанавливающих существование
таких точек, в которых функция или её
производная получает то или иное
среднее значение. Наиболее важной
теоремой о среднем значении функции
в дифференциальном исчислении является
теорема Лагранжа (теорема о конечном
приращении): если f(x) непрерывна на
отрезке [a,b] и дифференцируема в
интервале (a,b), то существует точка c,
принадлежащая интервалу (a,b), такая,
что f(b) − f(a) = (b − a)f'(c). В интегральном
исчислении наиболее важной теоремой
о среднем значении является следующая:
если f(x) непрерывна на отрезке [a,b], а
В
частности, если
Вследствие этого под средним значением функции f(x) на отрезке [a,b] обычно понимают величину
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
Билет 77. Формула Ньютона – Лейбница.
Если
функция f (x)
интегрируема на [a; b],
то для любого
который называется интегралом с переменным верхним пределом. Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если
функция f
интегрируема на [a; b]
и непрерывна в
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле. Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:
Пусть
функция f (x)
непрерывна на [a; b],
а F (x)
– какая-либо первообразная функции
f
на этом отрезке. Тогда
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть
f (x)
непрерывна на [a; b],
g (t)
имеет непрерывную производную на
[α; β],
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
Билет 78. Экономические приложения определенных интегралов.
Традиционно практическое приложение интеграла иллюстрируется вычислением площадей различных фигур, нахождением объемов геометрических тел и некоторыми приложениями в физике и технике. Однако роль интеграла в моделировании экономических процессов не рассматривается. Зачастую об экономических приложениях интеграла не идет речи и в классах экономического направления. Вместе с тем, интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике. Коэффициент Джини — статистический показатель, свидетельствующий о степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку (к примеру, по уровню годового дохода — наиболее частое применение, особенно при современных экономических расчётах). Рассчитать коэффициент можно как отношение площади фигуры, образованной кривой Лоренца и кривой равенства, к площади треугольника, образованного кривыми равенства и неравенства. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь 2ой. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1. Иногда говорят об индексе Джини как о процентном представлении коэффициента. Коэффициент можно рассчитать по формуле Джини:
где
G — коэффициент Джини, Xk — кумулированная
доля населения (население предварительно
ранжировано по возрастанию доходов),
Yk — доля дохода, которую в совокупности
получает Xk, n — число домохозяйств, yk
— доля дохода домохозяйства в общем
доходе,
Билет 79. Несобственный интеграл.
Несобственным
интегралом
Если предел стремящийся к правой части равенства (1), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся. По
аналогии с (1) определяется несобственный
интеграл на полуинтервале (-
Введем понятие
несобственного интеграла на интервале
(
Несобственным
интегралом
Аналогично
сводится понятие несобственного
интеграла от функции y=f(x)
непрерывной, но неограниченной на
(a;b] :
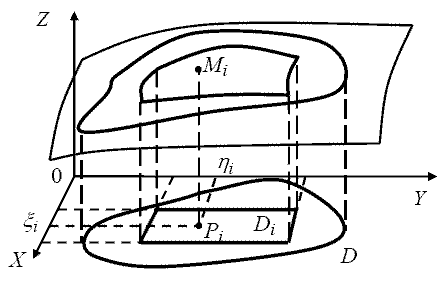
= Билет 80. Понятие двойного интеграла.
Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций.
Обозначение двойного интеграла.
Геометрический смысл двойного интеграла. Для того, чтобы понять, что же представляет из себя двойной интеграл с геометрической точки зрения, давайте посмотрим на рисунок ниже.
Итак, пусть в пространстве мы имеем некоторое тело (криволинейный цилиндр [в отличие от криволинейной трапеции в определенном интеграле]), ограниченное сверху поверхностью f(x,y), по бокам - некоторой цилиндрической поверхностью (образующие которой параллельны оси OZ), а снизу плоскостью X0Y. Не углубляясь особо в теорию, возьмем из нее главное: Геометрический смысл двойного интеграла: при неотрицательной функции f(x,y), двойной интеграл по области D представляет из себя объем криволинейного цилиндра, который построен на области D и ограничен сверху поверхностью z=f(x,y).
|

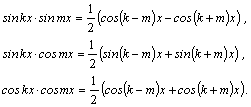

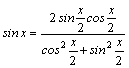 =[после
деления числителя и знаменателя
на
=[после
деления числителя и знаменателя
на 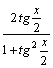 ;
;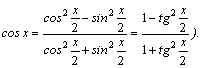
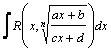 (под
знаком интеграла–рациональная функция
аргументов
(под
знаком интеграла–рациональная функция
аргументов 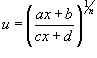 .
Интегрирование
иррациональных функций, содержащих
.
Интегрирование
иррациональных функций, содержащих