
- •Примеры экзаменационных заданий по математике
- •Алгебра и начала математического анализа Степени, корни.
- •Логарифмы
- •Основы тригонометрии
- •Свойства показательных и логарифмических функций
- •Показательные и логарифмические уравнения
- •Показательные и логарифмические неравенства
- •Функции, их свойства и графики
- •Нет правильного ответа.
- •3) 4) Нет правильного ответа.
- •Геометрия
- •4) Нет правильного ответа.
- •Элементы теории вероятностей
3) 4) Нет правильного ответа.
126.
Найдите значение определенного интеграла
![]()
1)
9; 2) 3![]() ;
3)
2;
4) 0.
;
3)
2;
4) 0.
127.Найдите
значение определенного интеграла ![]()
1) 1; 2) 6; 3) 0; 4) 3.
128.
Найдите значение определенного интеграла
![]()
1)
10; 2)
![]() ;
3)
;
3) ![]() ;
4) 4.
;
4) 4.
129.
Найдите значение определенного интеграла
![]()
1)![]() ;
2)
;
2)![]() ;
3)
;
3) ![]() ;
4) 48.
;
4) 48.
130.
Вычислить
определенный интеграл
![]()
1)
0; 2) 1; 3)
![]() ;
4)
;
4)
![]()
131.
Вычислить определенный интеграл
![]()
1) 6; 2) 8; 3) 2; 4) -1
Геометрия
132. Установите соответствие:
А) две прямые в пространстве называются параллельными;
Б) прямая и плоскость называются параллельными;
В) две прямые называются скрещивающимися;
Г) две плоскости называются параллельными;
1) если они не пересекаются;
2) если они не лежат в одной плоскости;
3) если они лежат в одной плоскости и не пересекаются;
4) если они не имеют общих точек.
133. Установите соответствие:
А) часть шара, отсекаемая от него какой-нибудь плоскостью, называется…..; Б) поверхность, полученная вращением полуокружности вокруг ее диаметра, называется …..;
В) тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов, называется……………;
Г) тело, полученное вращением прямоугольника вокруг одной из его сторон, называется……..
конусом; 2) цилиндром; 3) сферой; 4)шаровым слоем.
134. Установите соответствие:
А) боковыми гранями призмы являются….; Б) боковыми гранями пирамиды являются …..;
В) боковыми гранями усеченной пирамиды являются ……………;
Г) боковыми гранями прямоугольного параллелепипеда являются……..
1)трапеции; 2) параллелограммы; 3)прямоугольники; 4) треугольники.
135. Установите соответствие:
А) поверхность, составленная из 4 треугольников, называется…..; Б) поверхность, составленная из 6 параллелограммов, называется…..;
В) поверхность, составленная из многоугольников и ограничивающая геометрическое тело, называется…..;
Г) поверхность, составленная из 6 квадратов, называется …..
параллелепипед; 2) куб; 3) тетраэдр; 4) многогранник.
136. Укажите номера верных утверждений:
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна;
Любые четыре точки лежат в одной плоскости;
Прямая лежит в плоскости данного треугольника, если она пересекает две стороны треугольника;
Две плоскости имеют только 2 общие точки;
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Две прямые в пространстве называются параллельными, если они не имеют общих точек;
Любые четыре точки не лежат в одной плоскости;
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна;
Две плоскости имеют только 1 общую точку;
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Две прямые в пространстве называются скрещивающимися, если они лежат в одной плоскости;
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости;
Прямая лежит в плоскости данного треугольника, если она проходит через одну из вершин треугольника;
Две плоскости имеют только 1 общую прямую;
Любые три точки лежат в одной плоскости.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются;
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости;
Если две плоскости имеют общую точку, то они не пересекаются;
Два вектора равны, если равны их длины.
137. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые…
1) параллельные; 2)пересекающиеся; 3)скрещивающиеся; 4) перпендикулярные.
138. Если две прямые перпендикулярны к плоскости, то эти прямые…
1) перпендикулярные; 2) пересекающиеся; 3) скрещивающиеся; 4) параллельные.
139.
Прямая
а
лежит
в плоскости ![]() и пересекает плоскость β. Каково взаимное
расположение плоскостей
и пересекает плоскость β. Каково взаимное
расположение плоскостей ![]() и
β?
и
β?
1) они совпадают; 2) имеют только одну общую точку;
3) не пересекаются; 4) пересекаются по некоторой прямой.
140. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то ….
1) плоскости совпадают; 2) плоскости пересекаются;
3) плоскости параллельны; 4) плоскости имеют только одну общую точку.
141. Если две прямые параллельны третьей прямой, то они …………
1) равны; 2) параллельны; 3) скрещиваются; 4) пересекаются
142. Сколько общих точек могут иметь две различные плоскости?
1) 2; 2) несколько; 3) бесконечно много; 4) бесконечно много или ни одной.
143. Могут ли две различные плоскости иметь только две общие точки?
1) нет; 2) могут, но при дополнительных условиях; 3) всегда имеют; 4) нельзя ответить на вопрос.
144. Прямая называется перпендикулярной к плоскости....
Если она перпендикулярна к какой-нибудь прямой, лежащей в этой плоскости.
Если она перпендикулярна двум прямым, лежащим в этой плоскости.
Если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Если угол между ними равен 900.
145. Что можно сказать о взаимном расположении плоскостей, которые имеют три общие точки, не лежащие на одной прямой?
пересекаются; 2) параллельны; 3)ничего нельзя сказать; 4)совпадают.
146. Две параллельные плоскости пересечены третьей. Что можно сказать о линиях их пересечения?
пересекаются; 2) параллельны; 3) ничего нельзя сказать; 4) совпадают.
147. Через каждую из двух скрещивающихся прямых проходит плоскость…..
параллельная другой прямой;
пересекающая другую прямую;
параллельная другой прямой, и притом только одна;
скрещивающаяся с другой прямой, и только одна.
148. Двугранный угол – это….
фигура, образованная двумя плоскостями;
фигура, образованная прямой и двумя полуплоскостями;
фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости;
фигура, образованная гранями пирамиды.
149. Диагональ многогранника – это….
отрезок, соединяющий две вершины;
отрезок, соединяющий две противоположные вершины основания;
отрезок, соединяющий две вершины одной грани;
отрезок, соединяющий две вершины, не принадлежащие одной грани.
150. Апофема – это….
отрезок, соединяющий две вершины;
перпендикуляр, проведенный из вершины пирамиды к ее основанию;
высота пирамиды;
высота боковой грани правильной пирамиды, проведенная из ее вершины.
151. Высота пирамиды – это….
отрезок, соединяющий вершину пирамиды и ее основание;
перпендикуляр, проведенный из вершины пирамиды к ее основанию;
перпендикуляр, проведенный из вершины пирамиды к плоскости боковой грани;
перпендикуляр, проведенный из вершины основания к плоскости боковой грани.
152. Многогранник состоит из …
1) граней; 2) прямых; 3) точек; 4) другой ответ.
153. Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов А1А2В2В1, А2А3В3В2, …, АnА1В1Вn , называется …
1) пирамидой; 2) призмой; 3) усеченной пирамидой; 4) другой ответ.
154. Многогранник, составленный из n-угольника А1А2…Аn и n треугольников PА1А2, PА2А3, …, PАnА1 называется…
1) пирамидой; 2) призмой; 3) усеченной пирамидой; 4) цилиндром.
155. Боковыми гранями пятиугольной пирамиды являются:
1) пятиугольники; 2) параллелограммы; 3) трапеции; 4) треугольники.
156. Гранями правильного многогранника не могут быть:
1) треугольники; 2) четырехугольники; 3) пятиугольники; 4)шестиугольники.
157. Цилиндром называется …
1) тело, ограниченное цилиндрической поверхностью и кругом с границей L;
2) тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1;
3) тело, ограниченное конической поверхностью и кругом с границей L;
4) другой ответ.
158. Конусом называется …
1) тело, ограниченное конической поверхностью и кругом с границей L;
2) тело, ограниченное цилиндрической поверхностью и кругом с границей L;
3) тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1;
4) другой ответ.
159. Поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки, называется …
1) конусом; 2) цилиндром; 3) сферой; 4) шаром.
160. Осевым сечением цилиндра является:
1) треугольник; 2) параллелограмм; 3) трапеция; 4)прямоугольник.
161. Осевым сечением конуса является:
1) прямоугольный треугольник; 2) круг;
3) равнобедренный треугольник; 4) прямоугольник.
162. Часть шара, отсекаемая от него какой-нибудь плоскостью, называется …
1) шаровым сегментом; 2) шаровым слоем; 3) шаровым сектором; 4) другой ответ.
163. Часть шара, заключенная между двумя параллельными секущими плоскостями, называется …
1) шаровым сегментом; 2) шаровым сектором; 3) шаровым слоем; 4) другой ответ.
164. Тело, полученное вращением кругового сектора с углом, меньшим 900, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов, называется …
1) конусом; 2) шаровым сектором; 3) шаровым слоем; 4) другой ответ.
165.
Из тел, представленных на рисунке,
выбрать тела вращения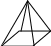
А .
Б.
В. Г.
.
Б.
В. Г.


1) А, Б, В; 2) Б, В; 3) А, Г; 4) Б, В, Г.
166. Из тел, представленных на рисунке, выбрать многогранники
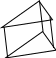

А .
Б.
В. Г.
.
Б.
В. Г.

1) А, Б, В; 2) Б, В; 3) А, Г; 4) А, В.
167.
Из тел, представленных на рисунке,
выбрать призмы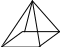

А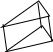

 .
Б.
В. Г.
.
Б.
В. Г.

1) А, Б; 2) А, Б, В; 3) Б, В; 4) В.
168. Площадь основания прямой треугольной призмы равна 30 см2, а высота призмы 10 см. Найдите площадь полной поверхности призмы, если периметр основания 40 см.
1) 400 см2; 2) 430 см2; 3) 460 см2; 4) 340 см2.
169. Сторона основания правильной треугольной призмы равна 7 см, а высота призмы 10 см. Найдите площадь боковой поверхности призмы.
1) 70 см2; 2) 105 см2; 3) 210 см2; 4) 329 см2.
170. Вычислите площадь полной поверхности правильной четырехугольной пирамиды со стороной 5 см. Высота боковой грани равна 7 см.
1) 140 см2 ; 2) 70 см2; 3) 95 см2; 4) 175 см2.
171. Стороны оснований правильной треугольной усеченной пирамиды равны 4 дм и 2 дм. Высота боковой грани 5 дм. Вычислите площадь боковой поверхности усеченной пирамиды.
1) 30 дм2; 2) 60 дм2; 3) 45 дм2; 4) 90 дм2.
172. Сторона основания правильной треугольной пирамиды равна 8 см. Высота боковой грани 9 см. Вычислите площадь боковой поверхности пирамиды.
1) 72 см2; 2) 108 см2; 3) 216 см2; 4) 230 см2.
173. Образующая конуса равна 5 см, а радиус основания 1 см. Чему равна площадь боковой поверхности конуса?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3) ![]() ;
4)
;
4) ![]() .
.
174.
Найдите площадь сферы, радиус которой
равен ![]() .
.
1)
2π м2;
2) 4π м2;
3)
8π м2;
4) ![]() м2.
м2.
175.
Чему равен объем шара, радиус которого
равен ![]() .
.
1)
36π м3;
2) 108π м3;
3) 9π м3;
4) ![]() м2.
м2.
176.Длины
ребер прямоугольного параллелепипеда,
имеющие общую вершину, равны 1 см, 2см и
![]() см.
Найдите диагональ параллелепипеда.
см.
Найдите диагональ параллелепипеда.
1)
3![]() ;
2)16; 3)
4;
4)
;
2)16; 3)
4;
4)![]() .
.
177.
Длины ребер прямоугольного параллелепипеда,
имеющие общую вершину, равны 2 см, 3 см и
![]() см.
Найдите объем параллелепипеда.
см.
Найдите объем параллелепипеда.
1)
10 см3;
2) 900 см3;
3)
30 см3;
4)![]() см3.
см3.
178. Высота цилиндра 8 дм, а диаметр – 6 дм. Найдите площадь осевого сечения цилиндра.
1) 24 дм2; 2) 48 дм2; 3) 64 дм2; 4) нет правильного ответа.
179. Радиусы оснований усеченного конуса 4 см и 16 см, а образующая - 6 см. Найдите площадь боковой поверхности усеченного конуса.
1) 60 см2; 2) 120π см2; 3) 120 см2; 4) 240π см2.
180. Сечение шара имеет площадь 36 см2. Радиус шара, если сечение удалено от его центра на расстояние 8 см, равен:
1)
![]() см; 2)
10 см;
3) 2 см; 4) 8 см.
см; 2)
10 см;
3) 2 см; 4) 8 см.
181. Объем шара вычисляется по формуле:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)![]() ;
4)
;
4)
![]()
182. Объем конуса вычисляется по формуле:
1)
;
2)
![]() ;
3)
;
4)
;
3)
;
4)
183. Объем призмы вычисляется по формуле:
1)
![]() ;
2)
;
3)
;
2)
;
3)![]() ;
4)
;
4)
184. Объем цилиндра вычисляется по формуле:
1)
;
2)
;
3)![]() ;
4)
.
;
4)
.
185. Объем пирамиды вычисляется по формуле:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
186. Площадь сферы вычисляется по формуле:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
Координаты и векторы в пространстве
187.Расстояние между двумя точками М1(x1; y1; z1) и M2(x2; y2; z2) вычисляется по формуле:
M1M2=(x2 – x1)2 + (y2 – y1)2+(z2 – z1)2;
M1M2=
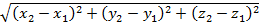 ;
;M1M2=
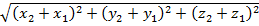 ;
;M1M2=
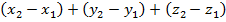 .
.
188.
Длина вектора ![]() вычисляется по формуле:
вычисляется по формуле:
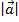 =
=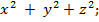
=
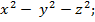
=
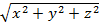 ;
;=
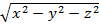 .
.
189.
Скалярное произведение векторов ![]() вычисляется по формуле:
вычисляется по формуле:
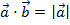 ·
·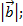
·
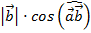 ;
;·
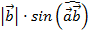 ;
;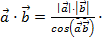
190.
Если вектор ![]() и вектор
и вектор ![]() ,
то разность векторов
,
то разность векторов ![]() имеет координаты:
имеет координаты:
191. Чему равны координаты точки С(x; y; z), которая является серединой отрезка АВ, если А(2; 4; 6) и В(-2; 4; 4)?
1) С(2; 4; 6); 2) С(-2; 4; 4); 3) С(0; 8; 10); 4) С(0; 4; 5).
192. Чему равно расстояние между точками А и В, если А(0; 2; 2) и В(1; 2; 4)?
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4) ![]()
193.
Дан вектор ![]() .
Укажите координаты вектора
.
Укажите координаты вектора ![]() ,
противоположного вектору
,
противоположного вектору ![]() .
.
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4) ![]()
194.
Вычислить косинус угла между векторами
![]() и
и ![]() .
.
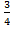 ;
2)
;
2)
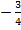 ;
3)
;
3) 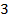 ;
4)
;
4)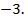
195. Вектором называется …
1) перпендикуляр, проведенный из любой точки пространства к данной прямой;
2) отрезок, для которого указано, какой из его концов считается началом, а какой – концом;
3) отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани;
4) другой ответ.
196. Компланарные векторы - это …
1) векторы, лежащие на одной прямой;
2) векторы, лежащие в параллельных плоскостях;
3) векторы, лежащие в параллельных плоскостях или в одной плоскости;
4) векторы, которые при откладывании их от одной и той же точки, будут лежать в одной плоскости.
197. Если скалярное произведение двух ненулевых векторов отрицательно, то угол между векторами …
1) острый; 2) прямой; 3) тупой; 4) нет правильного ответа.
198. Если скалярное произведение двух ненулевых векторов равно нулю, то угол между векторами …
1) острый; 2) прямой; 3) тупой; 4) нет правильного ответа.
199. Если скалярное произведение двух ненулевых векторов положительно, то угол между векторами …
1) острый; 2) прямой; 3) тупой; 4) нет правильного ответа.
200.Для любых трех точек А, В и С имеет место равенство:
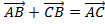 ;
2)
;
2) 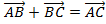 ;
3)
;
3) 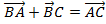 ;
4)
;
4) 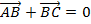 .
.
201.
Сумма векторов ![]() и
и ![]() есть вектор …
есть вектор …
1)![]() ;
2)
;
2)![]() ;
3)
;
3)
![]() ,
если KBCD
- параллелограмм;
4) нет правильного ответа.
,
если KBCD
- параллелограмм;
4) нет правильного ответа.
202. Разность векторов и есть вектор …
1) ; 2) ; 3) , если KBCD - параллелограмм; 4) нет правильного ответа.
203.
Если
![]() ,
то векторы
,
то векторы
![]() и
и
![]() …
…
1) равны; 2) одинаково направлены; 3) противоположны; 4) нет правильного ответа.
204.
Если
![]() и
и
![]() ,
то …
,
то …
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
