
- •Примеры экзаменационных заданий по математике
- •Алгебра и начала математического анализа Степени, корни.
- •Логарифмы
- •Основы тригонометрии
- •Свойства показательных и логарифмических функций
- •Показательные и логарифмические уравнения
- •Показательные и логарифмические неравенства
- •Функции, их свойства и графики
- •Нет правильного ответа.
- •3) 4) Нет правильного ответа.
- •Геометрия
- •4) Нет правильного ответа.
- •Элементы теории вероятностей
Функции, их свойства и графики
67. Числовой функцией называется …
множество всех точек (х; у) координатной плоскости;
подмножество координатной плоскости, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу;
соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х;
Нет правильного ответа.
68. Множество точек на координатной плоскости, абсциссы которых соответствуют значениям аргумента, а ординаты значениям функции, называется
1) функцией; 2) графиком; 3) криволинейной трапецией; 4) переменной.
69. Какая из функций является линейной?
1) у = х5 + 7х; 2) у = 5х; 3) у = 5х + 3; 4) у = 9х2 + 7х
70. Какая из перечисленных функций является линейной?
1) у = 5х + 7; 2) у = х2 + 5х; 3) у = х + 7; 4) у = 1 + х2
71. Графиком какой из функций является прямая?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
72. Графиком какой из функций является прямая?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
73. Графиком какой функции является гипербола?
1)
у = 2х + 5; 2) у = х2
– 7; 3)![]() ;
4)
;
4)
![]()
Область определения и область значения функции
74.
Найдите область определения функции у
=![]()
(-∞; 2]; 2) (-∞; 2); 3) (2; +∞); 4) [2; +∞).
75.
Найдите область определения функции у
=![]()
(-∞; 5]; 2) (-∞; 5); 3) (5; +∞); 4) [5; +∞).
76.
Найдите область определения функции
у
=![]()
1)![]() ;
2)
;
2)![]() ;
3) [-2;1]; 4)
;
3) [-2;1]; 4)![]() 2];
2];
5)
![]() .
.
77.
Найдите область определения функции у
=![]()
1)![]() ;
2)
;
2)![]() ;
3) (1; +
;
3) (1; +![]() ;
4)
;
4)![]() ∞)
∞)
78.
Укажите
область значения функции
![]()
1)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)![]()
79.
Укажите область определения функции
![]()
1)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
80.
Дана функция
![]() укажите область значений этой функции
укажите область значений этой функции
1) (-; +); 2) (0;+); 3) (1;+); 4) (-2;+)
81. Укажите область значений функции :
1) (-; +); 2) (0;+); 3) (1;+); 4) (-1;5)
82. Установите соответствие между названиями функций и формулами, которые их задают.
А) показательная функция;
Б) логарифмическая функция;
В) степенная функция;
Г) тригонометрическая функция.
1) у = 2х5+1;
2)
у =
![]()
3)
у
=
![]() +1;
+1;
4)
y
=
![]() .
.
83. Установите соответствие между следующими функциями и их областями значений.
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]() .
.
1) E(у) = [0; +∞);
2) E(у) = (0; +∞);
3) E(у) = [-1; 1];
4) E(у) = (-∞; +∞).
84. Установите соответствие между следующими функциями и их областью определения.
А)
![]() ;
;
Б)
![]() ;
;
В) ;
Г)
![]() .
.
1) D(x) =[0;+∞);
2) D(x) =(0;+∞)
3)
D(x)
=![]() ;
;
4) D(x) =(-∞;+∞)
Четность, нечетность
85. Какая из функций является четной?
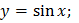 2)
2) 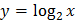 ;
3)
;
3) 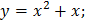 4)
4) 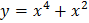 .
.
86. Какая из функций является четной?
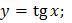 2)
2) 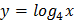 ;
3)
;
3) 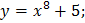 4)
4) 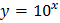 .
.
87. Какая из функций является четной?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
88. Какая из функций является нечетной?
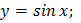 2)
2) 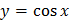 ;
3)
;
3) 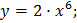 4)
.
4)
.
89. Какая из функций является нечетной?
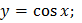 2)
2) 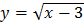 ;
3)
;
3) 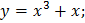 4)
4) 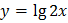 .
.
90. Какая из функций является нечетной?
1)![]() ;
2)
;
2)![]() ;
3)
;
4)
;
3)
;
4)
![]()
91. Какая из функций является нечетной?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
Возрастание и убывание функции
92. Какая из функций является убывающей на всей своей области определения?
1)![]() ;
2)
;
2) ![]() 3)
3)
![]() 4)
.
4)
.
93. Какая из функций является возрастающей на всей своей области определения?
1)![]() ;
2)
;
2)![]() 3)
3)![]() 4)
4)![]() .
.
94. Какая из функций является убывающей на всей своей области определения?
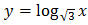 ;
2)
;
2) 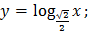 3)
3) 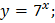 4)
.
4)
.
95. Какая из функций является возрастающей на всей своей области определения?
1)![]() ;
2)
;
2)![]() 3)
3)![]() 4)
4)![]() .
.
96. Какая из представленных функций является убывающей?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
97. Какая из функций является возрастающей?
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)![]() ;
4)
;
4)![]()
Исследование функции по графику
9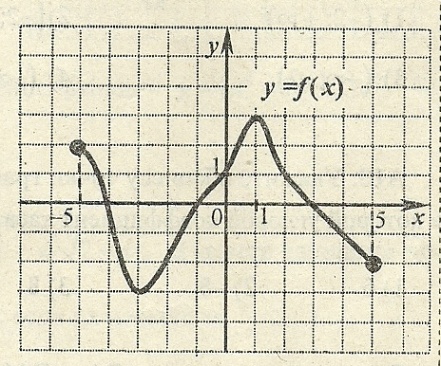 8.
На рисунке изображен график функции
8.
На рисунке изображен график функции
![]() ,
заданной на промежутке [-5; 5]. Каким
из перечисленных ниже свойств функция
не
обладает?
,
заданной на промежутке [-5; 5]. Каким
из перечисленных ниже свойств функция
не
обладает?
1) Наименьшее значение функции равно -3.
2) Функция не является ни четной, ни нечетной.
3) х = 1 – точка максимума функции.
4) Функция убывает на множестве [-5; -1].
9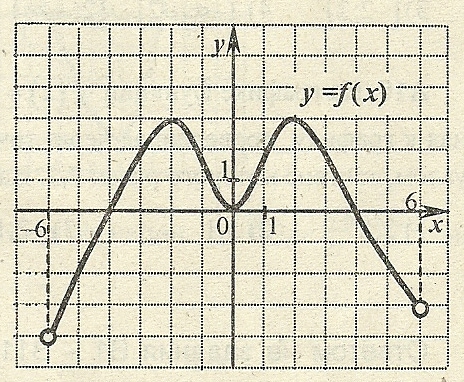 9.
На рисунке изображен график функции
,
заданной на промежутке (-6;6).
Каким из перечисленных ниже свойств
функция не
обладает?
9.
На рисунке изображен график функции
,
заданной на промежутке (-6;6).
Каким из перечисленных ниже свойств
функция не
обладает?
1) Наименьшее значение функции равно -3.
2)
На множестве (-6;-4)![]() функция принимает отрицательные
значения.
функция принимает отрицательные
значения.
3) х = 0 – точка минимума функции.
4) Функция четная.
1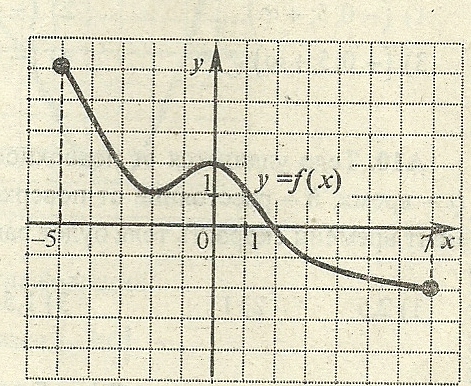 00.
На рисунке изображен график функции
,
заданной на промежутке [-5;
7].Каким из перечисленных ниже свойств
функция не
обладает?
00.
На рисунке изображен график функции
,
заданной на промежутке [-5;
7].Каким из перечисленных ниже свойств
функция не
обладает?
1) Функция не является ни четной, ни нечетной.
2)
Функция убывает на промежутке ![]()
3) Наименьшее значение функции равно .
4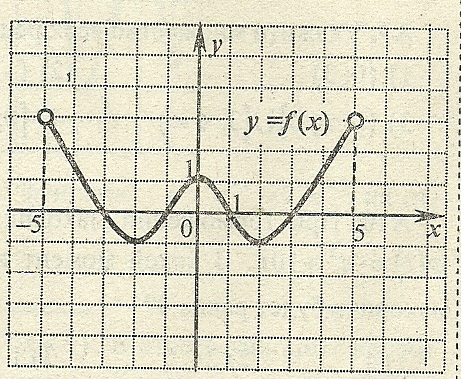 )
)![]() – точка минимума функции.
– точка минимума функции.
101. На рисунке изображен график функции , заданной на промежутке (-5; 5). Каким из перечисленных ниже свойств функция не обладает?
1) Функция четная.
2) Наибольшее значение функции равно 3.
3)
На множестве ![]() функция
принимает отрицательные значения
функция
принимает отрицательные значения![]()
4)![]() – точка максимума функции.
– точка максимума функции.
1 02.
График, изображенный на рисунке, является
графиком одной из перечисленных функций.
Укажите эту функцию.
02.
График, изображенный на рисунке, является
графиком одной из перечисленных функций.
Укажите эту функцию.
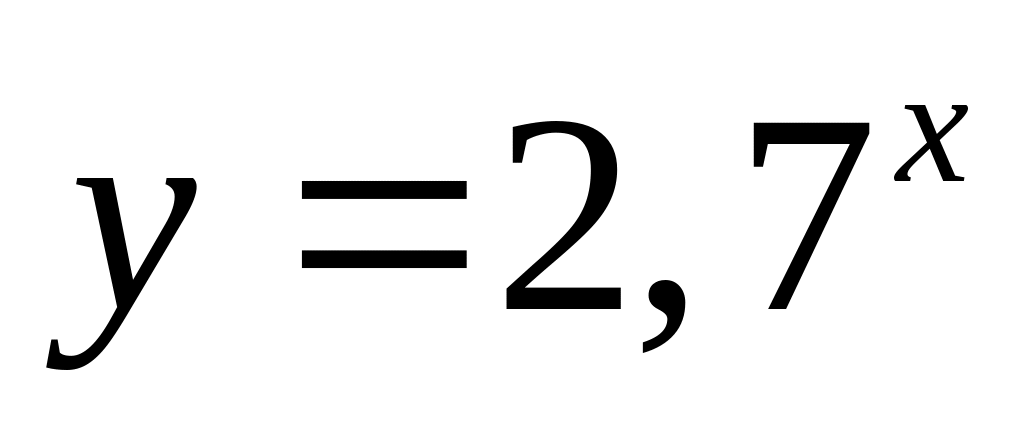 ;
;
 ;
;
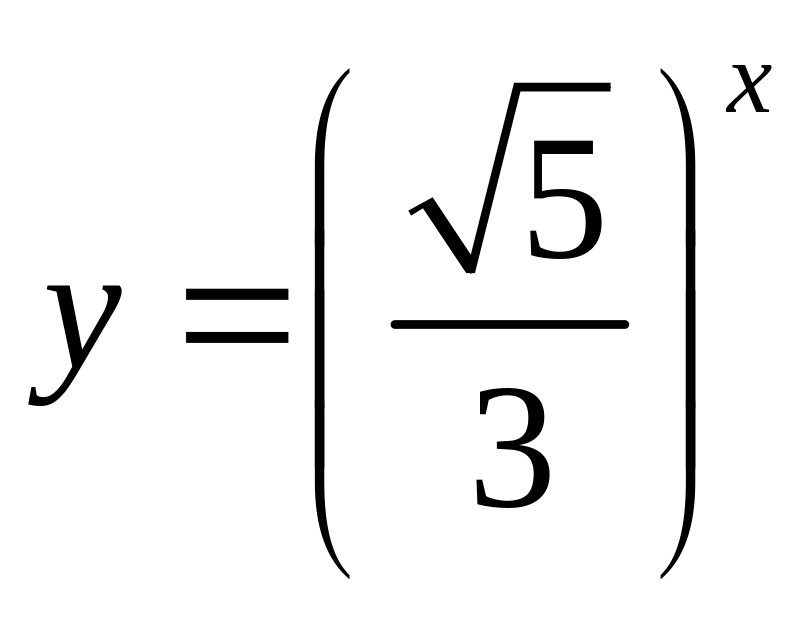 ;
;
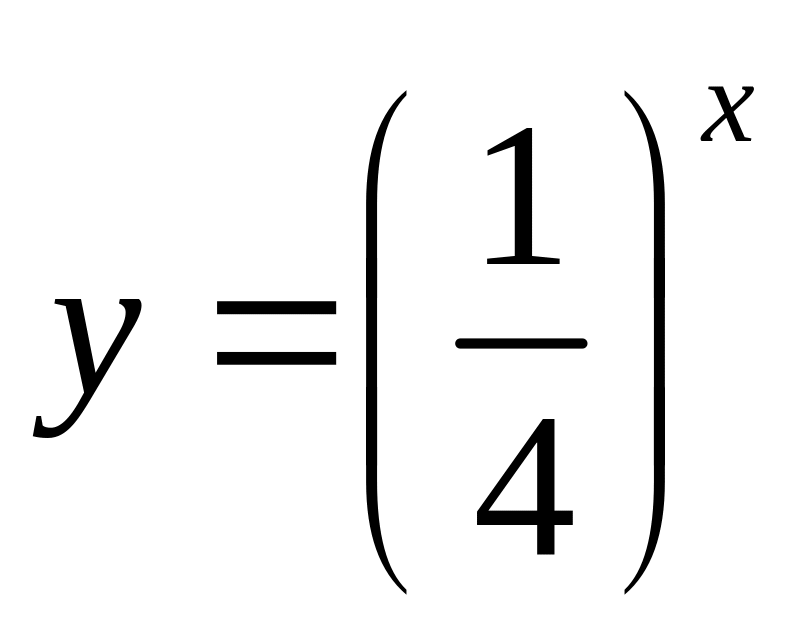 .
.
103.Функция, заданная формулой у = ах (где а>0, а ≠ 1), называется …
1) логарифмической; 2) показательной; 3) степенной; 4)нет правильного ответа.
Производная
104.
Критическими точками функции ![]() называют:
называют:
внутренние точки определения функции, в которых
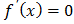 ;
;
внутренние точки определения функции, в которых
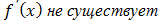 ;
;внутренние точки определения функции, в которых
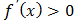 ;
;внутренние точки определения функции, в которых или
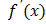 не существует.
не существует.
105.
Точка ![]() является точкой максимума функции
,
если:
является точкой максимума функции
,
если:
в точке производная функции не меняет знак;
в точке производная функции меняет знак с плюса на минус;
в точке производная функции меняет знак с минуса на плюс;
в точке производная функции не существует.
106. При каком условии функция возрастает?
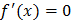 ;
2)
;
2) 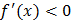 ;
3)
;
3) 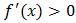 ;
4)
;
4)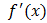 не существует.
не существует.
107. При каком условии функция убывает?
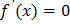 ;
2)
;
2) 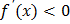 ;
3)
;
3)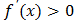 ;
4)
;
4)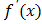 не существует.
не существует.
108.
Найдите производную функции у
=
х2·![]()
1)
у′
= 2х·![]() ;
2) у′
= х2·
;
2) у′
= х2·![]() - 2x·
;
- 2x·
;
3) у′ = 2x· + х2· ; 4) у′ = 2х· - x2·
109.
Найдите производную функции у
=![]()
1)
![]() ;
2)
;
2) ![]() ;
;
3)
![]() ;
4)
;
4) ![]()
![]()
110.
Найдите производную функции ![]()
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4) ![]() .
.
111.
Найдите производную функции
![]()
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
112.
Найдите тангенс угла наклона касательной
к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
1)
![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4) ![]() .
.
113. Найдите угловой коэффициент касательной, проведенный к графику функции у = 1,5х6 -2х2+4х+2 в его точке с абсциссой х0 =1
1) 11; 2) 6; 3) 9; 4) -9.
114.
Найдите тангенс угла наклона касательной
к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]()
1; 2) -π; 3) 3-0,25π2; 4) -5.
115.
Найдите угловой коэффициент касательной,
проведенный к графику функции
![]() в его точке с абсциссой х0
=
π
в его точке с абсциссой х0
=
π
1)
-1;
2) 0; 3) 1; 4)
![]() .
.
116.
Найдите
значение производной функции
![]() при х
= 2
при х
= 2
1) 3; 2) 1; 3) 2; 4) -2
117.
Найдите значение производной функции
![]() при х=
- 3
при х=
- 3
1) 36; 2) -79; 3) 12; 4) -25
118.
Определите производную функции
![]()
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
119.
Определите производную функции
![]()
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)
![]()
Первообразная и интеграл
120.
Укажите одну из первообразных для
функции ![]()
1)
![]() ;
2)
;
2) ![]() ;
;
3)![]() ;
4)
;
4)![]() ;
;
121.
Укажите одну из первообразных для
функции ![]()
1)
![]() ;
2)
;
2) ![]() ;
;
3)![]() ;
4)
;
4)![]() .
.
122.
Укажите одну из первообразных для
функции ![]() :
:
1)
![]() ;
2)
;
2)![]() ;
;
3)![]() ;
4)
;
4)![]() .
.
123.
Для какой функции функция![]() является первообразной?
является первообразной?
1)
![]() 2)
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
124.
Фигуру, ограниченную графиком функции
f,
непрерывной и не меняющей знака на
отрезке
![]() ,
отрезком
и прямыми
,
отрезком
и прямыми
![]() и
и
![]() ,
называют …
,
называют …
1) степенной функцией; 2) логарифмической функцией;
3) криволинейной трапецией; 4) нет правильного ответа.
125. Формула Ньютона – Лейбница имеет вид:
1)
![]() ;
2)
;
2)
![]()
![]()
