
- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
Свойства оператора набла
Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.
Если умножить вектор
на
скаляр
![]() ,
то получится вектор
,
то получится вектор
![]() ,
,
который представляет собой градиент функции .
Если вектор
скалярно
умножить на вектор
![]() ,
получится скаляр
,
получится скаляр
![]() ,
,
то есть дивергенция вектора .
Если умножить на векторно, то получится ротор вектора :
![]()
Замечание: как и для обозначения скалярного и векторного произведения вообще, в случае их применения с оператором набла, наряду с использоваными выше, часто используются эквивалентные им альтернативные обозначения, так, например, вместо
 нередко
пишут
нередко
пишут
 ,
а вместо
,
а вместо
 пишут
пишут
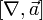 ;
это касается и формул, приводимых ниже.
;
это касается и формул, приводимых ниже.
Соответственно, скалярное произведение
![]() есть
скалярный оператор, называемый оператором
Лапласа. Последний
обозначается также
есть
скалярный оператор, называемый оператором
Лапласа. Последний
обозначается также
![]() .
В декартовых координатах оператор
Лапласа определяется следующим образом:
.
В декартовых координатах оператор
Лапласа определяется следующим образом:
![]()
Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:
![]()
![]()
То есть производная выражения, зависящего от двух полей, есть сумма выражений, в каждом из которых дифференцированию подвергается только одно поле.
Билет 44.2
Для удобства обозначения того, на какие поля действует набла, принято считать, что в произведении полей и операторов каждый оператор действует на выражение, стоящее справа от него, и не действует на всё, что стоит слева. Если требуется, чтобы оператор действовал на поле, стоящее слева, это поле каким-то образом отмечают, например, ставя над буквой стрелочку:
![]()
Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться.
Опера́тор Лапла́са
(лапласиа́н, оператор дельта) —
дифференциальный оператор, действующий
в линейном пространстве гладких функций
и обозначаемый символом
.
Функции
![]() он
ставит в соответствие функцию
он
ставит в соответствие функцию
 .
.
Оператор Лапласа эквивалентен
последовательному взятию операций
градиента
и дивергенции:
![]() ,
таким образом, значение оператора
Лапласа в точке может быть истолковано
как плотность источников (стоков)
потенциального
векторного поля
,
таким образом, значение оператора
Лапласа в точке может быть истолковано
как плотность источников (стоков)
потенциального
векторного поля
![]() в
этой точке. В декартовой системе координат
оператор Лапласа часто обозначается
следующим образом
в
этой точке. В декартовой системе координат
оператор Лапласа часто обозначается
следующим образом
![]() ,
то есть в виде скалярного произведения
оператора
набла на себя. Оператор
Лапласа унитарен.
,
то есть в виде скалярного произведения
оператора
набла на себя. Оператор
Лапласа унитарен.
Билет 45
Специальные виды векторных полей.
Потенциальное векторное поле.
называется потенциальным в области
G, если его можно
представить как градиент некоторого
скалярного поля U(M).
 Функция U(M) – потенциал
векторного поля
.
Функция U(M) – потенциал
векторного поля
.
 ;
;
;
;
 ;
;
 ;
;
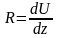 ;
;

Т.о. в потенциальной поверхностно односвязной области G поле обладает следубщими свойствами:
1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.

