
- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
3) Рациональные дроби.
Опр.
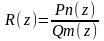 ,
где Pn(z),
Qm(z)
– многочлены,
наз. рациональной дробью.
,
где Pn(z),
Qm(z)
– многочлены,
наз. рациональной дробью.
n>=m – дробь неправильная; n<m – правильная.
Разложение правильной рац. дроби с комплексными коэф. на сумму простейших дробей.
Если
 - правильная дробь, то
- правильная дробь, то
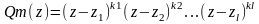 ,
где
,
где
z1, z2,…, zl – разл. компл. корни
k1, k2,…, kl – их кратности
то сущ. Такие компл. числа Aik, где i=1,2,…,l; k=1,2,…,ki, то тогда
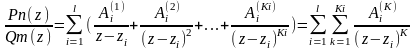
Разложение простой рац. дроби с действ. коэф. на сумму простейших дробей с действ. коэф.
Пусть
- правильная дробь,
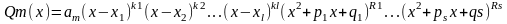
X1, x2,…, xl – разл. Компл. Корни
k1, k2,…, kl – их кратности
Билет 38.2
pi2-4qi<0 для i=1…s
R1, R2,…,Rs – кратности пар корней, тогда

+Метод неопределенных коэффициентов + Метод частных значений
Билет 39.
Условие независимости КРИ-2 от пути. Интегрирование полных дифференциалов.
Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны:
1)
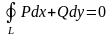 ,
где L – любой
замкнутый контур Д.
,
где L – любой
замкнутый контур Д.
2) Не зависит от пути ab.
3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \
4) dP/dy=dQ/dx в области Д.
Доказательство:

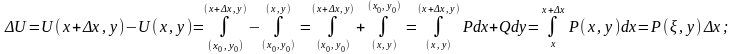
где
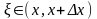 .
.
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.
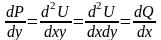
Нахождение ф-ции по ее полному дифференциалу.
Первый способ:
U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy
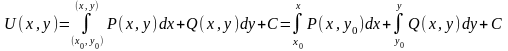
Второй способ:
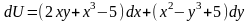 ;
;
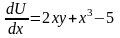

{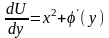 ;
;
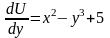 }
;
}
;

не зависит от пути.
Билет 40.
Физический смысл ПОВИ-2 – поток жидкости через пов-ть в единицу времени.
M (x,y,z) – вектор скорости жидкости. a (M) = P(x,y,z)i +Q (x,y,z)j + R(x,y,z)k
1)
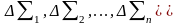 ;
;
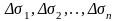 2)
2)
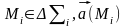
3)
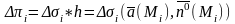 ;
4)
;
4)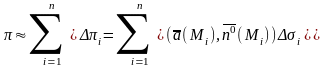
5)
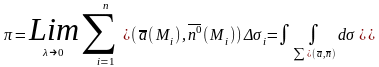
ПОВИ-2 есть поток жидкости (поток
векторного поля a(M))
через ориентированную поверхность .
.
Скалярная форма ПОВИ-2.
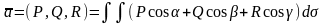 ;
;
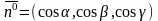 ПОВИ-1 для
ПОВИ-1 для
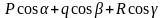 ;
;
ПОВИ-2 для P(x,y,z), Q(x,y,z), R(x,y,z) x,y,z-пректируемое
E, F(x,y,z)=0; x=x(y,z); y=y(x,z): z=z(x,y)
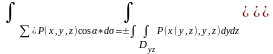
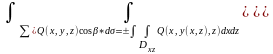

Замечания: если прямая, параллельная к-л из координатных осей пересекает поверхность более чем в одной точке, то пов-ть следует разбить на несколько пов-тей и воспользоваться свойством аддитивности ПОВИ-2.
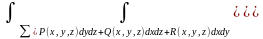 - ПОВИ-2
- ПОВИ-2
Формула Астроградского. Пусть
V-ограниченая
область, граница которой состоит из
конечного числа кусочно-гладких
поверхностей. Пусть ф-ции P,Q,R
и их частные производные dP/dx;
dQ/dy;
dR/dz
непрерывны в замкнутой области V,
тогда справедливо следуещее равенство:
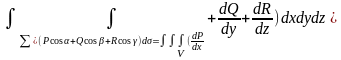
ПОВИ-2 берется по внешней стороне
пов-ти
 ,
ограниченной областью V.
,
ограниченной областью V.
Если пов-ть не замкнутая, но ее можно замкнуть простыми пов-ми, то дополнить, применить формулу Астроградского к замкнутой пов-ти, вычислить ПОВИ-2 по простым дополняющим пов-м и из интеграла по замкнутой пов-ти вычесть результат для дополнительных пов-тей.
Билет 41
Скалярные поля. Производная по направлению. Градиент.
Пусть V – некоторая
область в пространстве. Говорят, что в
этой области задано скалярное поле,
если каждой т.
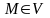 поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
Пусть U(M)
– некоторое скалярное поле.
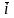 -
единственный фиксированный вектор.
-
единственный фиксированный вектор.
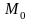 -фиксированая
точка.
-фиксированая
точка.
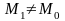 ;
;
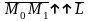 ;
;
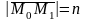
Если
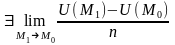 ,
то он называется производной скалярного
поля U(M)
по направлению
,
то он называется производной скалярного
поля U(M)
по направлению
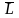 в точке
.
в точке
.

lnH-скорость изменения ф-ции U(m) по направлению в точке .
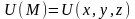 ;
;
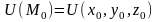 ;
;
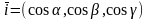 ;
;
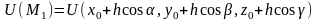 ;
;
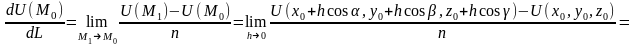
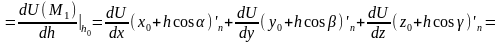
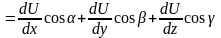
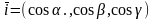 ;
;
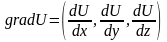 ;
;
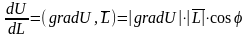 ;
;
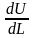 принимает наибольшее значение при
принимает наибольшее значение при
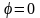 ,
т.е. в направлении вектора gradU
в т.
,
т.е. в направлении вектора gradU
в т.
gradU указывает направление наибольшего роста поля в данной точке. | gradU| - скорость роста ф-ции U в данном направлении. Вектро gradU не зависит от выбора системы координат. Grad направлен по поверхности уровня в данной точке.
Билет 42
Векторные поля и их основные характеристики.
Говорят, что в V
занадо векторное поле, если каждой т.
поставлен
в соответствие некоторый вектор
.
Физ. Векторные поля не зависят от выбора
СК.
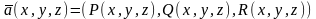
Векторная линия – кривая, в каждой точке M которой направлен по касательной к кривой. Векторная трубка – часть пространства, состоящая из целых векторных линий, каждая ВЛ или целиком лежит внутри этой трубки или находится вне ее.
Поток векторного поля. Дивергенция.
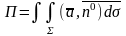
Дивиргенцией векторного поля
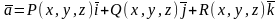 называется
скалярная ф-ция
называется
скалярная ф-ция
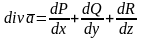 .
.
Формула Остроградского:

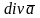 характеризует плотность источников
поля в данной точке. Не зависит от выбора
СК.
характеризует плотность источников
поля в данной точке. Не зависит от выбора
СК.
Формула Остроградского. Пусть V-ограниченая область, граница которой состоит из конечного числа кусочно-гладких поверхностей. Пусть ф-ции P,Q,R и их частные производные dP/dx; dQ/dy; dR/dz непрерывны в замкнутой области V, тогда справедливо следуещее равенство:
ПОВИ-2 берется по внешней стороне пов-ти , ограниченной областью V.
Если пов-ть не замкнутая, но ее можно замкнуть простыми пов-ми, то дополнить, применить формулу Астроградского к замкнутой пов-ти, вычислить ПОВИ-2 по простым дополняющим пов-м и из интеграла по замкнутой пов-ти вычесть результат для дополнительных пов-тей.
Билет 43
Циркуляция и ротор векторного поля.
Ротором (или вихрем) векторного поля
называется вектор-функция
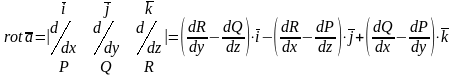
Ротор характеризует завихренность поля в данной точке.
Ротор является постоянным вектором, направленным вдоль оси вращения OZ. Его модуль равен удвоенной угловой скорости вращения тела.
Рассмотрим
.
С- кусочно гладкая пов-ть. КРИ-2
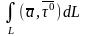 называется циркуляцией
называется циркуляцией
 вдоль кривой L в
направлении
вдоль кривой L в
направлении
 .
Если
-силовое
поле, то его циркуляция – работа вдоль
пути L.
.
Если
-силовое
поле, то его циркуляция – работа вдоль
пути L.
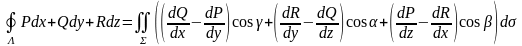
(формула Стокса).
Формула Стокса.
Пусть гладкая xyz-проетируемая
ориентированная поверхность
 ограничена кусочно гладким контуром
ограничена кусочно гладким контуром
 и пусть в некоторой 3х мерной области,
содержащей в себе поверхность
,
ф-ции P,Q,R
и их частные проихводные непрерывны,
тогда справедливо следующее:
и пусть в некоторой 3х мерной области,
содержащей в себе поверхность
,
ф-ции P,Q,R
и их частные проихводные непрерывны,
тогда справедливо следующее:
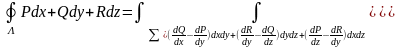 ,
,
где направление обхода контура осуществляется в положительном направлении.
Если граница состоит из нескольких контуров, то формула Стокса остается в силе. При этом в левой части надо написать сумму интегралов по всем контурам, пробегаемым в положительном направлении.
Для вычисления интегралов по замкнутому контуру можно выбрать любую поверхность , ограниченную контуром . Разумно выбирать поверхность простого вида.
Условие независимости КРИ-2 от пути интегрирования.
3х мерная область V называется поверхностно односвязной, если для любого замкнутого контура , лежащего в V внутри V найдется поверхность, ограниченная .
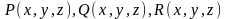 и
их частные производные 1го порядка
непрерывны в некоторой замкнутой
ограниченной поверхностью односвязной
области V, то след.
4 условия эквивалентны:
и
их частные производные 1го порядка
непрерывны в некоторой замкнутой
ограниченной поверхностью односвязной
области V, то след.
4 условия эквивалентны:
1)
любого
замкнутого кусочногладкого контура
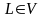 -
-
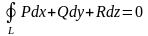
2)
 не
зависит от пути соединения точек А и В.
не
зависит от пути соединения точек А и В.
3)
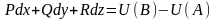 полный
диф-л, где
полный
диф-л, где
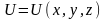
4)
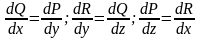
Билет 44
Опера́тор на́бла (оператор
Гамильтона) — векторный
дифференциальный
оператор, обозначаемый
символом
![]() (набла)
(набла)
![]()
Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа
