
- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
Аддитивность
Если сходится, то , ;
Линейность
Если сходится и сходится, то сходится и
Вычисление и преобразование НИ-2.
Формула Ньютона-Лейбница.
f(x) – непрерывна на [a.b); F(X) - некоторая первообразная.
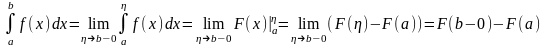
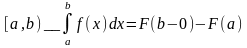
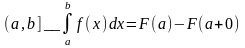
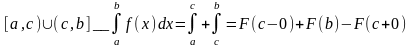
Интегрирование по частям.
Если U(x)
и V(x)
непр. И диф-мы на [a,b),
то
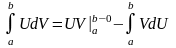
Исследование на сходимость.
{Аналогично НИ-1.}
Главное значении НИ-2.
f(x)
определено на
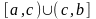
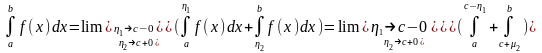
Определение:
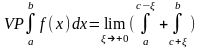
Билет 21.
Предел функции нескольких переменных.
Опр. т. А наз. пределом посл-ти (Mn)
если
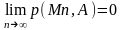 для любого Е(эпсилон) сущ. N-N(E);
любое n>=N(E)
=> p(Mn,A)
< E;
для любого Е(эпсилон) сущ. N-N(E);
любое n>=N(E)
=> p(Mn,A)
< E;
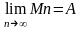 ;
;
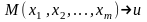 (число)
(число)
(x1, x2, …,xm)-независимые переменные.
Опр по Коши: число b наз
пределом ф-ии u=f(M)
в т. А (при
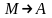 ),
если для любого Е > 0 сущ.
),
если для любого Е > 0 сущ.
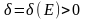 ,
для любого
,
для любого
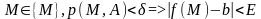
Опр по Гейне: число b наз
пределом посл-ти ф-ии u=f(M)
в т. А, если для любого (Mn),
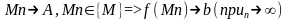
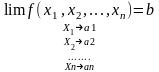 A(a1,
a2,…,
am)
A(a1,
a2,…,
am)
Теор. Если сущ.
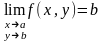 и
сущ.
и
сущ.
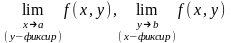 ,
то сущ.
,
то сущ.
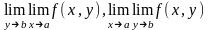 ,
причем
,
причем
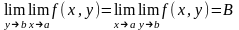
Опр. u=f(M)
наз. непрерывной в т. А, если
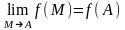
M(x1,
x2,
…,xn)
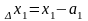 ;
;
 …
…
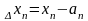 ;
A(a1,
a2,
…,an)
;
A(a1,
a2,
…,an)
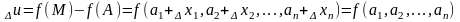
Опр2. u=f(M)
наз. непрерывной в т. А, если
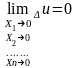
Точка в к-й ф-я не определена или не является непрерывной, наз. точками разрыва этой ф-ии.
Билет 22
Частные производные и их геометрический смысл.
Частная производная ф-ции
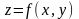 в
точке
в
точке
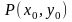 по
переменной x
называется
по
переменной x
называется
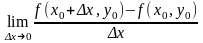 ,
если он
.
,
если он
.
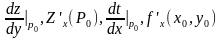 ;
;
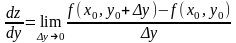 ;
;
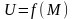 непрерывна
непрерывна
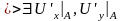
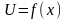 имеет частные производные в т. А,В
имеет частные производные в т. А,В
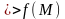 непрерывна
в т. А,В.
непрерывна
в т. А,В.
Билет 23.
Дифференцируемость ф-ций нескольких переменных.
Дифференциал.
;
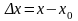 ;
;
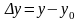
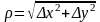 ;
;
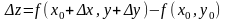
Ф-ция
называется
диф-м в точке
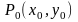 если ее полное приращение
если ее полное приращение
 может быть представлено в виде
может быть представлено в виде
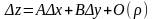 ,
где
,
где
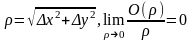 ,
А,В – числа.
,
А,В – числа.
Теорема: Если диф в точке , то непрерывна в этой точке.
Док-во: -диф-ма в т.
;
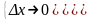
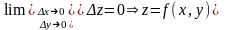 -
непрерывна в точке
-
непрерывна в точке
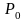
Теорема (необходимое условие диф):
Если
диф в точке
,
то
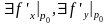
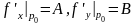
Док-во:
;
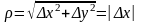 ;
;
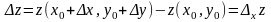
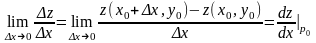
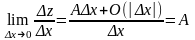
Теорема (достаточное условие диф): Если имеет частные производные в некоторой окрестности т. , непрерывна в самой точке , то она диф. В точке .
Если дифф. В т. , то главная линейная, относительно приращения аргумента, часть его полного приращения называется полным диффиринциалом ф-ции в т.
;
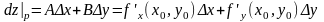
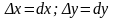 ;
;
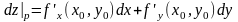 ;
;
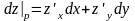 Рассмотрим функцию двух переменных
Рассмотрим функцию двух переменных
![]() ,
определенную в некоторой выколотой
окрестности точки
,
определенную в некоторой выколотой
окрестности точки
![]() .
Выберем и зафиксируем переменную
.
Выберем и зафиксируем переменную
![]() .
Получим функцию как бы одной переменной.
Рассмотрим предел:
.
Получим функцию как бы одной переменной.
Рассмотрим предел:
![]() Будем
считать, что
Будем
считать, что
![]() существует.
Теперь снимем фиксацию с переменной
и
рассмотрим следующий предел:
существует.
Теперь снимем фиксацию с переменной
и
рассмотрим следующий предел:
![]() Если
этот предел существует, то говорят, что
Если
этот предел существует, то говорят, что
![]() есть
повторный предел функции
в
точке
.
есть
повторный предел функции
в
точке
.
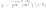
Аналогично мы можем фиксировать
сначала переменную
![]() .
В этом случае мы также получим повторный
предел, но, вообще говоря, другой:
.
В этом случае мы также получим повторный
предел, но, вообще говоря, другой:
![]() Это
определение можно распространить и на
функции нескольких переменных
Это
определение можно распространить и на
функции нескольких переменных
![]() .
.
Билет 24.
Диффиренцирование сложной ф-ции нескольких переменных.
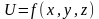 ;
;
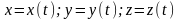 ;
;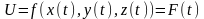
Теорема: Если ф-ция
дифф.
В т.
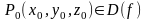 ,
а
,
а
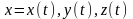 -
дифф. в т.
-
дифф. в т.
 ,
то тогда
,
то тогда
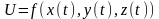 будет
дифф. в т.
и
будет
дифф. в т.
и
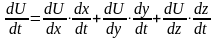
Док-во:
 ;
;
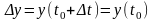 ;
;
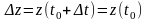
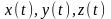 -
дифф. в т.
-
дифф. в т.
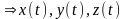 -
непрерывны в т.
-
непрерывны в т.
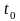 ,
т.е.
,
т.е.
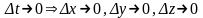 ;
;
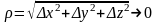
дифф.
в т.
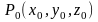
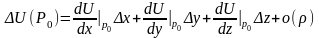
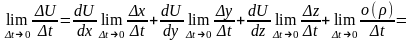
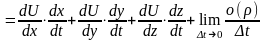 ;
;
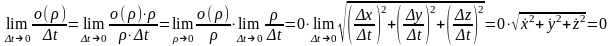
;
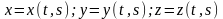 ;
;
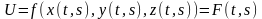 ;
;
;
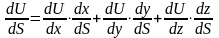
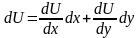 ;
;
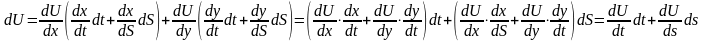
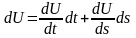 -
свойство инвариантности формы первого
дифф.
-
свойство инвариантности формы первого
дифф.
Билет 25 (Неявные функции)
Т.: (существования и дифференцируемости
неявной функции) Пусть функция одной
переменной у =![]() (х)
и независимая переменная х связаны
уравнением F(x, у) = 0, F(x, у) непрерывна в
окрестности т.
(х)
и независимая переменная х связаны
уравнением F(x, у) = 0, F(x, у) непрерывна в
окрестности т.![]() и имеет там непрерывные частные
производные
и имеет там непрерывные частные
производные![]() причем
причем![]()
![]() Тогда
уравнение F(x, y) = 0 определяет в окрестности
т.
Тогда
уравнение F(x, y) = 0 определяет в окрестности
т.![]() функцию
у = у(х), которая имеет непрерывную
производную Доказательство дано в [11.
С. 449, 452].
функцию
у = у(х), которая имеет непрерывную
производную Доказательство дано в [11.
С. 449, 452].
Выведем при условиях теоремы формулу для нахождения производной неявной функции у = у(х), заданной уравнением F(x, у) = 0:
![]() (11.3)
(11.3)
По правилу дифференцирования сложной
функции продифференцируем F(x, у):![]() отсюда
следует (11.3)
отсюда
следует (11.3)
Пример:![]()
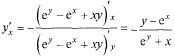
Формулы для нахождения производных
функции z = z(x, у), заданной неявно
уравнением![]() приведены
в ОК № 11.
приведены
в ОК № 11.
Пример:![]()
![]()
Билет 26
