
- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
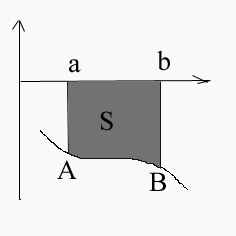
В декартовой системе координат
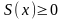
 f(x)-непрерывна
f(x)-непрерывна
x=a,x=b; отр [a,b] оси оХ
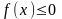
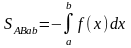
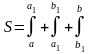
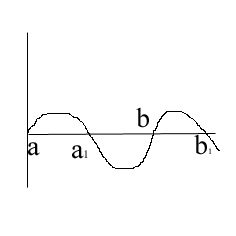
В параметрическом виде.
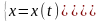
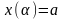


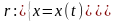
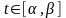 ;
;
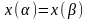 ;
;
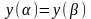
разбиваем:
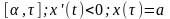 ;
;
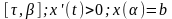

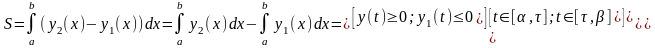
В полярной системе координат
 ;
;
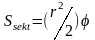 ;
;
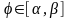 ;
;
 ;
;
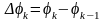
 ;
;
 ;
;
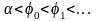
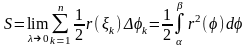
Билет 16
Вычисление длинны дуги с помощью определённого интеграла
Пусть известна функция
![]() и
требуется найти длину дуги, заданной
функцией
,
где
и
требуется найти длину дуги, заданной
функцией
,
где
![]() .
.
Для определения длины дуги
![]() необходимо
вычислить определенный
интеграл:
необходимо
вычислить определенный
интеграл:

Рассмотрим случай параметрического задания кривой:
где
![]() .
В этом случае для определения длина
дуги
вычисляется
определенный
интеграл:
.
В этом случае для определения длина
дуги
вычисляется
определенный
интеграл:
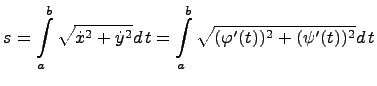
Рассмотрим случай, когда кривая
задается в полярных координатах
![]() где
где
![]() .
Тогда для определения длины дуги
вычисляется
следующий определенный
интеграл:
.
Тогда для определения длины дуги
вычисляется
следующий определенный
интеграл:
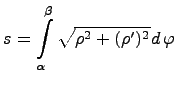
Билет 17
Вычисление объемов тел: Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны Mixi и mixi здесь xi = xi - xi-1.
Произведя
такие построения для всех отрезков
разбиения, получим цилиндры, объемы
которых равны соответственно
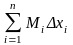 и
и
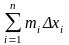 .При
стремлении к нулю шага разбиения ,
эти суммы имеют общий предел:
.При
стремлении к нулю шага разбиения ,
эти суммы имеют общий предел:
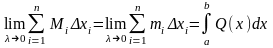 Таким образом, объем тела может быть
найден по формуле:
Таким образом, объем тела может быть
найден по формуле: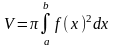
Билет 18.
Определение НИ-1.
Пусть f(x) определена на
 и инт на
и инт на
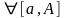
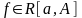 ;
;
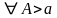 ,
т.е.
,
т.е.
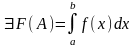
Пусть
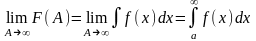
Если этот lim существует и конечен, то говорят, что НИ-1 сходится. Если не существует или бесконечен, то расходится.
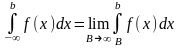 ;
;
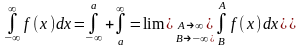
Свойтсва НИ-1.
Аддитивность
Если
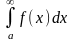 сходится, то
сходится, то
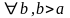 ,
,
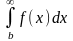 ;
;
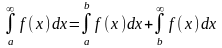
Линейность
Если
сходится и
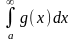 сходится, то
сходится, то
 сходится и
сходится и
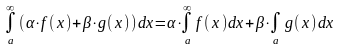
Вычисление и преобразование НИ-1.
Формула Нбютона-Лейбница.
Если f(x)
непрерывна на
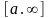 и F – какая-то
первообразная для ф-ции f(x),
то
и F – какая-то
первообразная для ф-ции f(x),
то
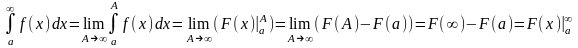
Интегрирование по частям.
Если U,V
– непрер. Диф-мы ф-ции на
,
то
Исследование на сходимость.
Т1: Пусть ф-ции f(x)
и g(x)
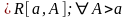 ,
тогда если
,
тогда если
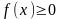 и
и
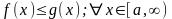 ,
то
,
то
сходится
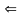 сходится
сходится
расходится пасходится
Предельный признак сравнения для НИ-1.
Т2: Пусть
,
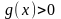
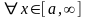 ;
;
 ,
тогда если
,
тогда если
 конечный
конечный
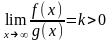 ,
то
и
сходятся или расходятся одновременно.
,
то
и
сходятся или расходятся одновременно.
При k=1
 при
при
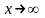
Т3: Если
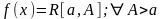 и
и
 сходится, то
сходится.
сходится, то
сходится.
Определение: называется абсолютно сходящимся, если сходится .
Если расходится, а сходится, от - неабсолютно (условно) сходящийся .
Билет 18.2
Главное значении.
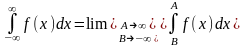
Главным значением
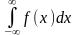 называется
называется
 ;
VP-Value
principul
;
VP-Value
principul
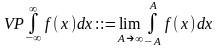
Если
 и сходится, то
и
и сходится, то
и
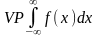
Билет 19.
Определение НИ-2.
f(x)
определена на [a,b);
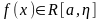 ;
;
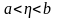 ,
т.е.
,
т.е.
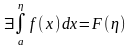
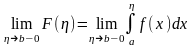 называется НИ-2 и обозначается
называется НИ-2 и обозначается
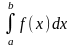
Если этот Lim существует и конечен, то говорят, что сходится. Если он не сущ-т или бесконечен, то НИ-2 расходится.
Свойства НИ-2.
{Аналогично НИ-1. }
