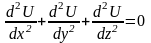- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
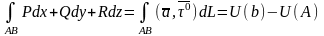
3) Потенциальное поле является безвихревым
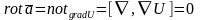
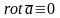 - необходимое и достаточное условие
потенциальности поля
в поверхностно односвязной области.
- необходимое и достаточное условие
потенциальности поля
в поверхностно односвязной области.
Билет 46
Сопеноидальное векторное поле.
Векторное поле
называется сопеноидальным в области
G, если в этой
области
 (нет
источников).
(нет
источников).
 ;
;
 ;
;
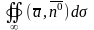 ;
;
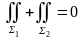 ;
;
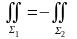 ;
;
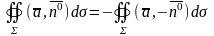 ;
;
Закон сохранения интенсивности векторной трубки в сопеноидальном поле.
В сопеноидальном поле
поток через любое сечение векторной
трубки имеет одно и тоже значение.
Векторные линии в соп. поле не могут
начинаться или заканчиваться внутри
областисопеноидальности.
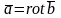 -это
поле является соп-м.
-это
поле является соп-м.
Любое физ векторное поле C
может быть представлено в виде суммы
и
 ,
где
-потенциальное,
-соленоидальное.
,
где
-потенциальное,
-соленоидальное.
Гармоническое векторное поле.
гармоноческое, если оно является одновременно потенциальным и сопеноидальным.
 ;
;
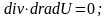
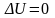 ;
;