
- •X1, x2,…,xn – действ. Корни
- •Оба нечетные или четные -
- •1) P z, тогда , где s-общий знаменатель дроби
- •6. (Аддитивность опред. Ин-ла)
- •9. Если f(X)r [a,b], то |f(X)|r [a,b]
- •В декартовой системе координат
- •В параметрическом виде.
- •В полярной системе координат
- •Аддитивность
- •Линейность
- •Аддитивность
- •Линейность
- •Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Замена переменных в тройном интеграле.
- •1. Поверхность s задана уравнением
- •2. Поверхность s задана параметрически:
- •Скалярная форма кри-2
- •3) Рациональные дроби.
- •X1, x2,…, xl – разл. Компл. Корни
- •2) Не зависит от пути ab.
- •Свойства оператора набла
- •1) Циркуляция потенциального вдоль любого замкнутого контура равна нулю.
- •2) Для любых т. А,в из области g циркуляция потенциального поля не зависит от выбора кривой ав, а зависит только от выбора а и в.
- •3) Потенциальное поле является безвихревым
Билет 1.
Комплексные числа.
Комлексным числом Z
наз. число z=x+iy,
где x, y
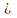 R.
R.
Мн-во
 комплексных
чисел – С, R
C, x–действ.
часть, y – мнимая
часть.
комплексных
чисел – С, R
C, x–действ.
часть, y – мнимая
часть.
Расстояние от z(x,y)
до начала корд. наз.
модулем комп. числа
Z.
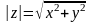 Аргументом
числа Z
0,
наз угол
Аргументом
числа Z
0,
наз угол
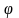 ,
кот-й образует радиус-вектор точки Z
и полож направл оси OX.
,
кот-й образует радиус-вектор точки Z
и полож направл оси OX.
Argz = argz
(главное знач аргумента) + 2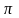 k
k
Z
k
k
Z
- <argz<
argz =
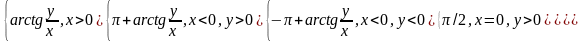
z = x+iy=zcos +izin =z(cos +isin )
z=r(cos + isin ) (!)
z1 = r1(cos + isin )
z2 = r2(cos + isin ) тогда
z1*z2 = r1*r2(cos( 1+ 2) + isin( 1+ 2)
zn = rn(cos(n ) + isin(n )
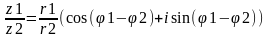
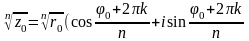 - Формула Муавра (!)
- Формула Муавра (!)
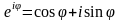
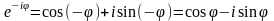
Формулы Эйлера:
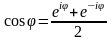 ;
;
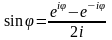 (!)
(!)
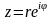 ;
;
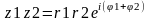 ;
;
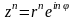 ;
;
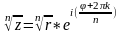
Билет 2.
Многочлены.
Многочлен (полином) относительно
переменной z - это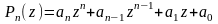
2z4-5z3+2z=(z2-1)(2 z2-5z+2)+(-3z-2)
Qm(z) Tk(z) Rc(z)
Значит Pn(z) = Qm(z) Tk(z) + Rc(z) (*), где m<=n m+k=n, l<n;
Если Rc(z) = 0, то Pn(z) делится на Qm(z).
Назовем компл. число z1 корнем многочл. Pn(z), если Pn(z1).
Теор. БЕЗУ: многочлен не нулевой степени Pn(z) делится на двучлен z-z1, тогда и только тогда, когда z1 является корнем Pn(z).
Запишем (*) для Pn(z) и z-z1: Pn(z) = (z-z1)Tn-1(z)+ Rc(z) => z:=z1.
Основная теорема алгебры(Гаусса): всякий многочлен Pn(z) не нулевой степени имеет по крайней мере 1 комплексный корень.
Компл. число z1 наз. корнем кратности к1 многочл. Pn(z), если
Pn(z) = (z-z1)к1Тn-k1(z)
Следствие: Многочл. Pn(z) имеет n комлексных корней с учетом их кратности:
Pn(z) = an(z-z1)к1(z-z2)к2…
Пусть z1
– корень Pn(z)
с действ. коэф-ми, тогда
 корень
Pn(z)
корень
Pn(z)
Pn(
)=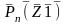 =
=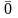 =0
=0
Комплексно-сопряж. корни входят в разложение многочлена парами.
(z-z1)(z- )=z2+p1z+q1
Pn(x) – с действ. коэф.
Pn(x)=an(x-x1)k1(x-x2)k2*…*(x-xl)kl(x2+p1x+q1)R1(x2+p2x+q2)R2*…*(x2+pmx+qm)Rm
X1, x2,…,xn – действ. Корни
k1, k2,…,kn – их кратности
P1, P2,…,Pn, q1, q2,…,qn – действ. числа
k1+k2+…+kl+2R1+2R2+…+2Rm = n
Билет 3
(рациональные дроби и их разложение на суммы простейших дробей методы нахождения коэффицентов разложения)
Пусть
знаменатель правильной рациональной
дроби
![]() может
быть представлен в виде
может
быть представлен в виде![]()
![]() (множителей
вида
(множителей
вида![]() может быть несколько), где
может быть несколько), где
![]() —
заданные числа
—
заданные числа![]()
![]() трехчлен
трехчлен![]() не
имеет действительных корней.
не
имеет действительных корней.
Тогда![]() представляется
в виде суммы простейших дробей
представляется
в виде суммы простейших дробей
1—3 типов:
![]()
![]()
где![]() —
неизвестные коэффициенты, которые
находятся путем приведения суммы справа
к общему знаменателю и последующего
приравнивания полученного числителя
к
—
неизвестные коэффициенты, которые
находятся путем приведения суммы справа
к общему знаменателю и последующего
приравнивания полученного числителя
к![]() Доказательство
представлено в [3. С.354].
Доказательство
представлено в [3. С.354].
Примеры:
1)![]()
2)![]()
3)![]()
Два метода нахождения коэффициентов в разложении рассмотрим на примере.
Пример:
![]()
Поскольку![]() (см.
пример в
(см.
пример в
п. 16.1.1), то
![]()
Правильную рациональную дробь под интегралом представим в виде суммы простейших:
![]()
![]() (16.1)
(16.1)
Первый метод — метод неопределенных коэффициентов — заключается в приравнивании коэффициентов при одинаковых степенях х в (16.1):
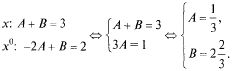
Второй метод — метод частных значений — заключается в подстановке значений х в (16.1), в первую очередь, корней знаменателя:
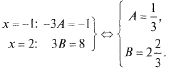
Окончательно имеем
![]()
Билет 4.
Понятие первообразной ф-ции и неопределенного интеграла.
Пусть ф-ция f(x) определена на X. Ф-ция F(x) – первообразная для f(x) на X, если F’(x)=f(x) для любого x € X.
F(x) – первообразная, F(x)+C – первообразная.
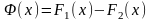
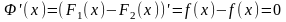 для
для
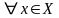
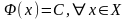 ;
;
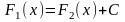
Совокупность всех первообразных
F(x)+C
для ф-ции f(x),
определенное на X,
называется неопределенным интегралом
от ф-ции f(x)
на X и обозначается

 ;
;
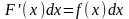
Основные свойства неопределенного интеграла.
1).
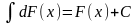
2).

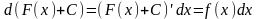
3).
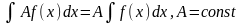
4).


Билет 5.
Замена переменной в неопределенном интеграле.
Внесение множителя под знак диффиринциала.
Теорема: Пусть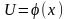 определена
и диф-ма на X. U-
множество значений ф-ции
.
Для f(U)
существует F(U)
на U.
определена
и диф-ма на X. U-
множество значений ф-ции
.
Для f(U)
существует F(U)
на U.
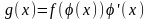 Тогда для g(x)
на X сущ-т
первообразная
Тогда для g(x)
на X сущ-т
первообразная
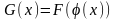 ,
т.е.
,
т.е.
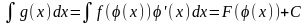
Док-во:
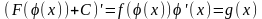
На практике:
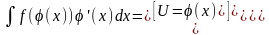
Вынесение множителя из-под знака дифференциала.
Теорема: Пусть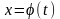 определена и диф-ма на T.
определена и диф-ма на T.
 на
Т. Для g(t)
на Т существует G(t).
на
Т. Для g(t)
на Т существует G(t).
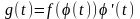 ,
тогда для f(x)
на X существует
первообразная
,
тогда для f(x)
на X существует
первообразная
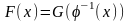 .
.
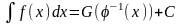
Док-во:
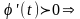 возрастающая
возрастающая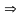 гарантировано
гарантировано
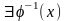 (обратная).
(обратная).
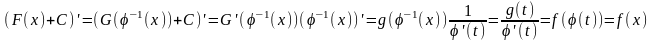
На практике:
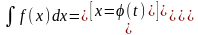
Билет 6.
Интегрирование по частям в неопределённом интеграле.
Т. Пусть функции U(x)
и V(x)
непрерывны на некотором промежутке X,
дифферинциируемы в его внутренних
точках и на Х существует
 ,
тогда
,
тогда
На Х существует
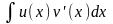 ,
причем
=
u(x)v(x)-
,
или
,
причем
=
u(x)v(x)-
,
или
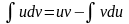 ;
;
Док-во:
d(uv)=vdu+udv;
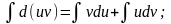

Билет Интегрирование рациональных функций.
Интеграл от многочлена – легко и просто. Правильная рациональная дробь раскладывается на сумму элементарных дробей.
Типы дробей:
1)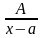 ,
2)
,
2) ,3)
,3)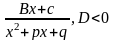 ,4)
,4)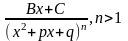
1)

2)
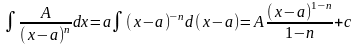
3)
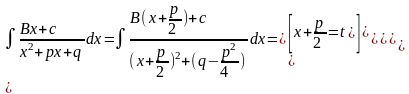
4)
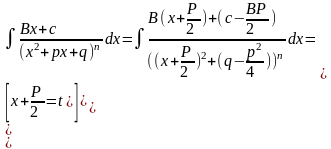
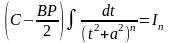 - рекуррентная формула
- рекуррентная формула
Вывод: интеграл от любой рациональной ф-ции выражается элементарной ф-цией ln,arctg, степенная.
Билет 7
Напомним, что рациональной
алгебраической функцией называется
дробь, в которой числитель и знаменатель
являются многочленами с вещественными
коэффициентами. Обозначим рациональную
дробь через
![]() ,
где
,
где
![]() и
и
![]() многочлены
степени
многочлены
степени
![]() и
и
![]() соответственно.Рассмотрим
случай, когда степень числителя больше
или равна степени знаменателя, т.е.
соответственно.Рассмотрим
случай, когда степень числителя больше
или равна степени знаменателя, т.е.
![]() .
Разделим многочлен
на
многочлен
с
остатком, получим, что
.
Разделим многочлен
на
многочлен
с
остатком, получим, что
![]() ,
где
,
где
![]() -многочлен
степени
-многочлен
степени
![]() ,
,
![]() -
многочлен степени
-
многочлен степени
![]() .
.
Далее заметим, что при интегрировании
![]() можно
без особого труда проинтегрировать
.
Перейдем к рассмотрению неопределенного
интеграла от
можно
без особого труда проинтегрировать
.
Перейдем к рассмотрению неопределенного
интеграла от
![]() .
Хорошо известно, что многочлен можно
разложить на линейные и квадратические
множители. Поступим таким образом со
знаменателем, т.е.
.
Хорошо известно, что многочлен можно
разложить на линейные и квадратические
множители. Поступим таким образом со
знаменателем, т.е.
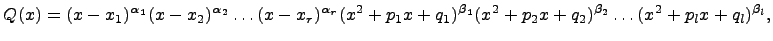
где
![]() ,
-
степень знаменателя, т.е. многочлена
.
Тогда рациональная дробь
разлагается
на сумму элементарных дробей следующим
образом:
,
-
степень знаменателя, т.е. многочлена
.
Тогда рациональная дробь
разлагается
на сумму элементарных дробей следующим
образом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Коэффициенты
![]() ,
,
![]() и
и
![]() находятся
методом неопределенных коэффициентов.
находятся
методом неопределенных коэффициентов.
Далее интегрируя каждую из полученных дробей, получаем ответ.
Проинтегрируем первые дроби. Достаточно рассмотреть следующий интеграл:
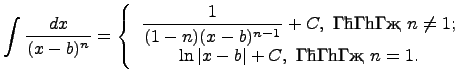
Билет 8.
Интегрирование тригонометрических функций.
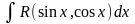
tg(x/2)=t – универсальная тригоном. подстановка.
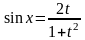 ;
;
 ;
;
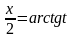 ;
;
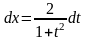
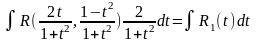
Специальная тригоном. подстановка:
R(-sinx,cosx)dx = -R(sinx,cosx), тогда cosx = t;
R(sinx,-cosx)dx = -R(sinx,cosx), тогда sinx = t;
R(-sinx,-cosx)dx = -R(sinx,cosx), тогда tgx = t;
Интегралы вида:
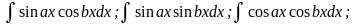
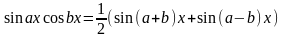
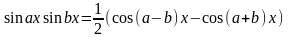
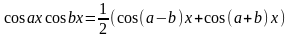
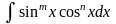
m,n Z, m,n >= 0;
