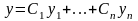- •18. Определение производной функции в точке.
- •19. Определение дифференцируемой функции в точке x0 .
- •20. Определение дифференциала функции f(X ) в точке x0 .
- •41. Достаточное условие интегрируемости.
- •42. Геометрический смысл определенного интеграла.
- •43. Свойства определенного интеграла.
- •49. Определение несобственного интеграла от неограниченной функции на ограниченном промежутке.
- •51.Окрестность точки в Rn . Внутренние и граничные точки множества.
- •52. Открытые и замкнутые множества.
- •53.Изолированные и предельные точки множества.
- •54.Ограниченные множества.
- •81.Сведение кратного интеграла к повторному интегралу.
- •82. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.
- •83. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.
- •84. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.
- •85. Числовые ряды.
- •86. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.
- •87. Свойства сходящихся рядов.
- •88. Необходимое условие сходимости числового ряда.
- •89. Числовые ряды с неотрицательными членами.
- •90. Критерий сходимости числовых рядов с неотрицательными членами.
- •91. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.
- •92. Знакопеременные ряды. Абсолютная и условная сходимость.
- •97. Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости.
- •107. Общее решение однородного дифференциального уравнения с
- •109. Общее решение однородной системы линейных
97. Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости.
Пусть функция f(x) разлагается на интервале (-R, R) в степенной ряд f(x)= а0+а1+а2x2+…+аnxn+…. Рассмотрим степенной ряд а1+2а2x+…+nаnxn-1+…, полученный почленным дифференцированием ряда f(x)= а0+а1+а2x2+…+аnxn+…. Тогда: 1) ряд а1+2а2x+…+nаnxn-1+… имеет тот же радиус сходимости R, что и ряд f(x)= а0+а1+а2x2+…+аnxn+…; 2) на всем интервале (-R, R) функция f(x) имеет производную f`(x), которая разлагается в степенной ряд а1+2а2x+…+nаnxn-1+….
Если функция f(x) разлагается в степенной ряд на интервале (-R, R), то она интегрируема в этом интервале. Интервал от суммы ряда равен сумме интегралов от членов ряда.
98. Ряды Тейлора (Маклорена)
Пусть
функция f(x)
определена в некоторой окрестности
точки x=0
и имеет в этой точке производные всех
порядков. Степенной ряд
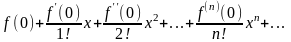 называют рядом Маклорена для функции
f(x).
называют рядом Маклорена для функции
f(x).
99. Достаточное условие разложимости функции в ряд Маклорена
Пусть
функция f(x)
определена и бесконечно дифференцируема
в интервале (-r,
r).
Если существует такая константа М, что
во всех точках указанного интервала
выполняются неравенства
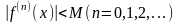 ,
то в этом интервале ряд Маклорена
сходится к функции f(x).
,
то в этом интервале ряд Маклорена
сходится к функции f(x).
100. Разложение в ряд Маклорена функций
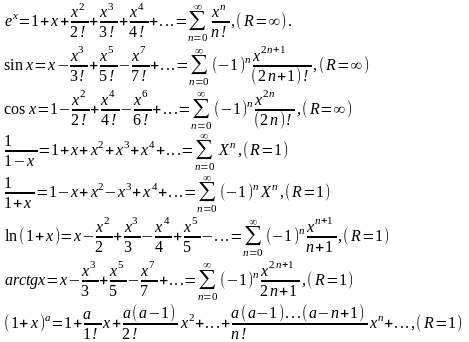
101. Теорема о существовании и единственности решения задачи
Коши для уравнения первого порядка в нормальной форме.
Если в некоторой
окрестности точки
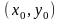 функция f(x,y)
определена, непрерывна и имеет непрерывную
частную производную
функция f(x,y)
определена, непрерывна и имеет непрерывную
частную производную
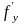 ,
то существует такая окрестность точки
,
в которой задачи Коши
,
то существует такая окрестность точки
,
в которой задачи Коши
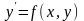 ,
,
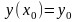 имеет решение, притом единственное.
имеет решение, притом единственное.
Если задача Коши , имеет единственное решение, то это решение называется частным решением уравнения .
102. Уравнения с разделяющимися переменными. Автономные
уравнения.
Уравнения
с разделяющимися переменными. Это
дифференциальные уравнения вида:
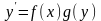 ,
где f(x)
и g(x)
– непрерывные функции. Запишем это
уравнение в форме:
,
где f(x)
и g(x)
– непрерывные функции. Запишем это
уравнение в форме:
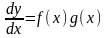 .
Для отыскивания решения этого уравнения
необходимо, как говориться, разделить
в нем переменные, т.е. переписать уравнение
следующим образом:
.
Для отыскивания решения этого уравнения
необходимо, как говориться, разделить
в нем переменные, т.е. переписать уравнение
следующим образом:
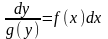 в
предположении, что в рассматриваемой
области
в
предположении, что в рассматриваемой
области
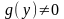 .
Теперь левая часть уравнения содержит
только переменную y,
а правая – только x.
Интегрируя обе части этого уравнения
получим:
.
Теперь левая часть уравнения содержит
только переменную y,
а правая – только x.
Интегрируя обе части этого уравнения
получим: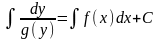 .
Таким образом, найден общий интеграл
уравнения.
.
Таким образом, найден общий интеграл
уравнения.
Частным
случаем является автономное уравнение
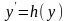 Его
интегральные кривые при параллельном
переносе вдоль оси абсцисс переходят
друг в друга.
Его
интегральные кривые при параллельном
переносе вдоль оси абсцисс переходят
друг в друга.
103. Однородные дифференциальные уравнения первого порядка.
Дифференциальное
уравнение
называется
однородным, если функция f(x,y)
является однородной нулевой степени,
т.е. для любого t
> 0 область определения функции содержит
точки (tx,ty)
и выполнено равенство f(tx,ty)
= f(x,y).
При
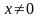 такое
уравнение заменой
такое
уравнение заменой
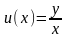 можно свести к уравнению с разделяющимися
переменными.
можно свести к уравнению с разделяющимися
переменными.
104. Уравнения в полных дифференциалах.
Уравнение
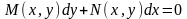 называется
уравнением в полных дифференциалах,
если существует такая непрерывно
дифференцируемая функция U(x,y),
что dU
= M(x,y)dy
+ N(x,y)dx.
Поскольку
называется
уравнением в полных дифференциалах,
если существует такая непрерывно
дифференцируемая функция U(x,y),
что dU
= M(x,y)dy
+ N(x,y)dx.
Поскольку
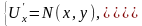 то
равенство
то
равенство
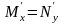 означает,
что данное уравнение будет уравнением
в полных дифференциалах. Тогда функцию
U(x,y)
находим интегрированием уравнений
системы
.
Общий интеграл уравнения
записывается в виде U(x,y)
= C.
означает,
что данное уравнение будет уравнением
в полных дифференциалах. Тогда функцию
U(x,y)
находим интегрированием уравнений
системы
.
Общий интеграл уравнения
записывается в виде U(x,y)
= C.
105. Линейные дифференциальные уравнения первого порядка.
Уравнения Бернулли.
Дифференциальное
уравнение вида
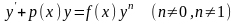 называется
уравнением Бернулли. Заменой
называется
уравнением Бернулли. Заменой
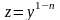 уравнение
Бернулли приводится к линейному уравнению
уравнение
Бернулли приводится к линейному уравнению
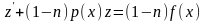
106. Линейные дифференциальные уравнения. Фундаментальная
система решений. Определитель Вронского системы решений.
В
данном параграфе мы остановимся на
свойствах частного и общего решения
линейного однородного дифференциального
уравнения n-го
порядка: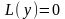
1.
Лемма 2.Пусть
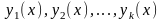 -
произвольные
решения линейного однородного
дифференциального уравнения и
-
произвольные
решения линейного однородного
дифференциального уравнения и
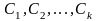 -
произвольные
постоянные, тогда линейная комбинация
-
произвольные
постоянные, тогда линейная комбинация
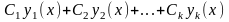 также
является решением этого уравнения.
также
является решением этого уравнения.
Пусть
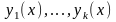 -
система,
состоящая из К функций, тогда определитель
Вронского этой
системы имеет вид:
-
система,
состоящая из К функций, тогда определитель
Вронского этой
системы имеет вид: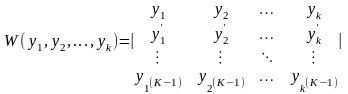
Справедливы следующие утверждения.
Теорема
7.7.
Если
функции
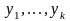 линейно
зависимы, то их определитель Вронского
тождественно равен нулю.
линейно
зависимы, то их определитель Вронского
тождественно равен нулю.
Теорема 7.8. Если - линейно независимые решения уравнения , то их определитель Вронского ни при одном значении х не обращается в нуль.
Определение.
Систему
функций
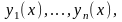 ,
состоящую из п линейно независимых
решений уравнения
,
будем
называть фундаментальным
набором решений этого
уравнения.
,
состоящую из п линейно независимых
решений уравнения
,
будем
называть фундаментальным
набором решений этого
уравнения.
Теорема
7.9 (об
общем решении линейного однородного
уравнения), Пусть
- фундаментальный набор решений уравнения
,
тогда
общее решение этого уравнения задается
формулой