
- •1.3. Твердые растворы
- •1.Экстремумы функций. Возрастание и убывание функций.
- •2.Выпуклость, точки перегиба, асимптоты графика функций.
- •3.Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов.
- •4.Замена переменной в неопределенном интеграле. Метод интегрирования по частям.
- •8.Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.
- •5.Определенный интеграл и его геометрический смысл.
- •6.Основные свойства определенного интеграла.
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •14.Производные и дифференциалы высших порядков для функций многих переменных. Формула Тейлора
- •16.Площадь фигуры и объём тела
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
1.3. Твердые растворы
Твердые растворы (ТР) - кристаллические фазы переменного состава, в которых атомы элемента В размещаются в пространственной решетке элемента А, не изменяя ее типа.
Для ТР характерен металлический тип межатомной связи. Твердые растворы обозначают: , , , или А(В). Твердые растворы всегда более тверды, чем чистые металлы, менее пластичны. Их образование всегда сопровождается увеличением электрического сопротивления, как правило, снижаются пластичность и вязкость. Твердые растворы бывают упорядоченными и неупорядоченными. Твердые растворы, устойчивые при сравнительно низких температурах, получили название упорядоченных твердых растворов, или сверхструктур. Полностью упорядоченные растворы образуются в том случае, когда отношение компонентов в сплаве равно целому числу: 1:1, 1:2, 1:3 и т.д. Они занимают промежуточное положение между твердыми растворами и химическими соединениями. При изменении температуры происходит разупорядочение ТР с соответствующим изменением свойств. Температуру разупорядочения к называют точкой Курнакова. Упорядоченные твердые растворы обозначают буквами ’, ’, ’, ’. Все металлы могут в той или иной степени взаимно растворяться друг в друге в твердом состоянии. В тех случаях, когда компоненты могут замещать друг друга в кристаллических решетках в любых количественных соотношениях, образуется непрерывный ряд твердых растворов. Твердые растворы замещения с неограниченной растворимостью могут образоваться при соблюдении следующих условий: 1. Компоненты должны обладать одинаковыми по типу (изоморфными) кристаллическими решетками. 2. Различие в атомных размерах компонентов должно быть не значительным и не превышать 8 – 15 %. 3. Компоненты должны принадлежать к одной и той же группе периодической системы элементов или к смежным родственным группам и в связи с этим иметь близкое строение валентной оболочки электронов в атомах.
13.Дифференцируемость
функции многих переменных. Производная
по направлению. Градиент.
U=f(x)
диф-ма в точке х, если её приращение
можно представить в виде:
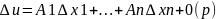 ,
где p=
,
где p=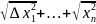 .
Теорема.
U=f(x)
диф-ма в точке х, тогда она в этой точке
имеет частные производные по всем
переменным и её диф-л опред.: du=
.
Теорема.
U=f(x)
диф-ма в точке х, тогда она в этой точке
имеет частные производные по всем
переменным и её диф-л опред.: du=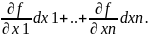 Теорема
2. Если u=f(x)
имеет в х частные производные, непрерывные
в некоторой окружности точки х, тогда
ф-ция u=f(x)
диф-ма в точке х.
Док-во:
Теорема
2. Если u=f(x)
имеет в х частные производные, непрерывные
в некоторой окружности точки х, тогда
ф-ция u=f(x)
диф-ма в точке х.
Док-во:
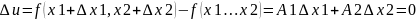 Производная
по направлению. Градиент.
Пусть
u=f(x,y,z),(x,y,z)
Производная
по направлению. Градиент.
Пусть
u=f(x,y,z),(x,y,z)
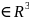 ,
l(l1,l2,l3)-вектор.
,
l(l1,l2,l3)-вектор.
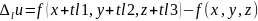 -
приращение вдоль направления L.Производной
ф-ции u
по нaправлению
L
наз-ют предел
-
приращение вдоль направления L.Производной
ф-ции u
по нaправлению
L
наз-ют предел
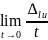 и обоз-ют
и обоз-ют
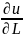 .
Вектор
.
Вектор
 наз-ют градиентом ф-ции u=f(xn)
и обозначают grad
f=
grad
u.
Cв-ва:
наз-ют градиентом ф-ции u=f(xn)
и обозначают grad
f=
grad
u.
Cв-ва:
grad(
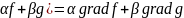
grad (fg)= g grad f+ f grad g
grad h(f)=
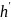 (f)
grad f
(f)
grad f
14.Производные и дифференциалы высших порядков для функций многих переменных. Формула Тейлора
Для
функции y=f(x)
производной порядка n
называют производную производной
порядка n-1.
Обозначают
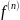 (x),
(x),
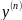 .
Теорема.
Если u=f(x)
имеет на некотором множ-ве D
.
Теорема.
Если u=f(x)
имеет на некотором множ-ве D непрерывные частные производные до
n-порядка
включительно, то она наз-ся n-раз
непрерывно диф-ой на множ-ве D.
непрерывные частные производные до
n-порядка
включительно, то она наз-ся n-раз
непрерывно диф-ой на множ-ве D.
Дифференциалом
порядка n
функции наз-ют диф-л от дифференциала
порядка n-1.
Обозначают
 .
Диф-ом нулевого порядка считают
.
Диф-ом нулевого порядка считают
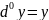 .
.
Формула
Тейлора.
Пусть функция f(x)
имеет в точке а все производные до
порядка n
включительно. Представление f(x)
в виде : f(x)=
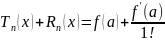 (x-a)+
(x-a)+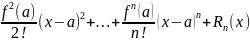 -наз-ют
формулой Тейлора порядка n
в точке a.
Остаточным многочленом формулы Тейлора
наз-ют разность
-наз-ют
формулой Тейлора порядка n
в точке a.
Остаточным многочленом формулы Тейлора
наз-ют разность
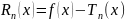 ,
где
,
где
 -
Многочлен Тейлора.
-
Многочлен Тейлора.
15.Экстремум
функции многих переменных
Безусловный экстремум
Точка x0,
y0
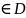 наз-ся точкой локального min(max),
если сущ. Такая окрестность U(x0,y0)
этой точки, что f(x,y)
наз-ся точкой локального min(max),
если сущ. Такая окрестность U(x0,y0)
этой точки, что f(x,y)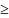 f(x0,y0),
f(x0,y0),
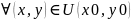 Теорема.
Если u=f(x,y)
имеет в x0,y0
локальный экстремум и диф-ма в этой же
точке, то
Теорема.
Если u=f(x,y)
имеет в x0,y0
локальный экстремум и диф-ма в этой же
точке, то
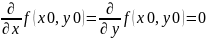 .
Теорема.
Пусть
u=f(x0,y0)
диф-ма в окрестности точки x0,y0
и дважды диф-ма x0,y0.
Обозначим
.
Теорема.
Пусть
u=f(x0,y0)
диф-ма в окрестности точки x0,y0
и дважды диф-ма x0,y0.
Обозначим
![]()
D=a11a22-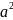 12
Тогда
если: 1) D>0,то
ф-ция имеет локальный экстремум
2) D<0-экстремума
нет
3) D=0-
требуются дополнительные исследования
Условный экстремум (x0,y0)
12
Тогда
если: 1) D>0,то
ф-ция имеет локальный экстремум
2) D<0-экстремума
нет
3) D=0-
требуются дополнительные исследования
Условный экстремум (x0,y0)
 наз-ся точкой условного лок-ого min(max),
если сущ-ет такая окрестность U,
что f(x,y)
f(x0,y0),
f(x,y)
наз-ся точкой условного лок-ого min(max),
если сущ-ет такая окрестность U,
что f(x,y)
f(x0,y0),
f(x,y) f(x0,y0),
(x,y)
U(x0,y0)/
Задача отыскания точек условного эк-ма
равносильна поиску точек безусловного
эк-ма, так наз-ой ф-ции Лангранжа:
-составим ф-цию:
f(x0,y0),
(x,y)
U(x0,y0)/
Задача отыскания точек условного эк-ма
равносильна поиску точек безусловного
эк-ма, так наз-ой ф-ции Лангранжа:
-составим ф-цию:
![]()
где ![]() - вектор Лангранжа.
- вектор Лангранжа.
-Составим систему из уравнений
-Если полученная система имеет решение, то есть решение исходной задачи
16.Площадь фигуры и объём тела
Под
фигурой в
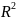 будем понимать любое множество точек.
Прямоугольник П=
будем понимать любое множество точек.
Прямоугольник П= .
Площадь будем обозначать
.
Площадь будем обозначать
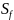 ,
тогда площадь прямоуг.
,
тогда площадь прямоуг.
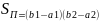 .
.
Фигура
F
наз. эл-ой, если она сост. из конечных
прям-ов Пi,
которые имеют общие точки возможно
лишь на границе. Элементарные фигуры
 ,
,
 наз.
соответственно описанными и вписанными
в фигуру D,
если
наз.
соответственно описанными и вписанными
в фигуру D,
если
 .Внутренняя
площадь S
-sup,
внешняя S
-inf.
Фигура D
наз. квадрируемой, когда площадь её
границы равна 0.
.Внутренняя
площадь S
-sup,
внешняя S
-inf.
Фигура D
наз. квадрируемой, когда площадь её
границы равна 0.
Объём.
Под телом в
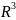 будем понимать произвольное множество
точек. Параллелепипед P=
будем понимать произвольное множество
точек. Параллелепипед P= .
.
 .
Эл-ым телом F
наз. тело сост. из объединения конечного
числа парал.Fi,
которые имеют общие точки возможно
лишь на границе.
.
Эл-ым телом F
наз. тело сост. из объединения конечного
числа парал.Fi,
которые имеют общие точки возможно
лишь на границе.
 ,
,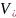 наз. соответственно описан. и вписанным
в тело D,
если
наз. соответственно описан. и вписанным
в тело D,
если
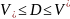 .
Внутренний
наз. sup,
внешний
-inf.
Тело D
будет кубируемым , когда объём его
границы равен 0.
.
Внутренний
наз. sup,
внешний
-inf.
Тело D
будет кубируемым , когда объём его
границы равен 0.
19.Тройной интеграл.
Если сущ.
Конечный предел
 не зависящий от разбиения
не зависящий от разбиения
 и выбора
точек (
и выбора
точек (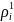 ,
, )
)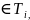 то
этот предел назыв.
тройным интегралом
и обозна-ся
то
этот предел назыв.
тройным интегралом
и обозна-ся
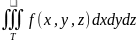 Тройной
интеграл изучают и используют по
аналогам с двойным. Аналогично двойному
интегралу сущ. формулы,позволяющие
перейти от тройного интегр. к повторному(или
двойному) Например,если T-парал-ед,
а
Тройной
интеграл изучают и используют по
аналогам с двойным. Аналогично двойному
интегралу сущ. формулы,позволяющие
перейти от тройного интегр. к повторному(или
двойному) Например,если T-парал-ед,
а
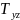 -его
проекция на плоскость
-его
проекция на плоскость
 ,
то тройной интеграл
=
,
то тройной интеграл
=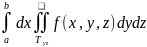 =
=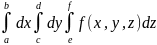
Пусть
ф-ция f(x,y,z)непрерывна
на D,тогда
тройной интеграл по D ,
,
где
I(u,v,w)-матрица
Якоби отображения
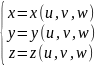 ,(u.v.w)
,(u.v.w)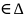 Отметим
основные классы интегрирования ф-ции:
Отметим
основные классы интегрирования ф-ции:
1.непрерывные на компакте 2.оганиченные и непрерывные на мн-ве D,за исключением подмножества мн-ва D,объем которого равен 0.
3. произведение интегрируемых ф-ций.
20.Криволинейный
интеграл первого рода, формула его
вычисления. Определение
1.
Интегральной
суммой для функции f
(x;
y)
по дуге AB
называется сумма вида:
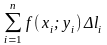 .
Определение
2.
Криволинейным
интегралом от функции f
(x;
y)
по дуге AB
(или криволинейным интегралом I
рода) называется предел интегральной
суммы
вида
.
Определение
2.
Криволинейным
интегралом от функции f
(x;
y)
по дуге AB
(или криволинейным интегралом I
рода) называется предел интегральной
суммы
вида
 при условиях:
при условиях:
1)
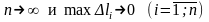 ;
2) этот предел существует и не зависит
ни от способа разбиения дуги AB
на части, ни от выбора на каждой из
частей точек
;
2) этот предел существует и не зависит
ни от способа разбиения дуги AB
на части, ни от выбора на каждой из
частей точек
 .
Теорема.Пусть
ф-ция x(t),y(t),z(t)
определяющие кривую
.
Теорема.Пусть
ф-ция x(t),y(t),z(t)
определяющие кривую
 непрерывно
дифференцир-мы,тогда криволин. интеграл
можно вычислить по фbормуле
непрерывно
дифференцир-мы,тогда криволин. интеграл
можно вычислить по фbормуле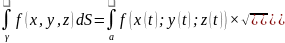 dt
dt
21.Свойства криволинейного интеграла первого рода. 1.Св-во линейности
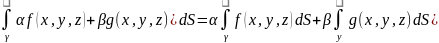
2.Если
f(x,y,z)
g(x,y,z),то
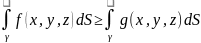
3.
Если кривая
сост. из 2-х частей
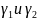 ,то
,то
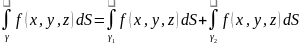
4.Если
m
f(x,y,z)
5.(теорема о среднем значении)
Если
f(x,y,z)
непрерывна на кривой
,а
f-длина
кривой
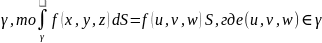
17.Определение двойного интеграла и его свойства Пусть D – некоторая замкнутая ограниченная плоская область, т.е. множество D ⊂ R^2 и пусть функция двух переменных f ( x,y ) определена во всех точках области D. D=D1 ∪D2 ∪… ∪Dn = ∪Di , и обозначим площадь i-ой части через ∆Si = S(Di). Выберем в каждой части Di по точке Mi(xi,yi) и составим интегральную сумму ∑ f(xi,yi) ∆Si . Если существует конечный предел этих интегральных сумм при λ → 0 , не зависящий от способа разбиения области D и выбора точек Mi, то этот предел называется двойным интегралом от функции f (x,y) по области D, и обозначается: ∫∫ f(x,y)dxdy Теорема . Если множество D замкнуто ограниченно и связно, а функция f (x,y) непрерывна на множестве D, то есть точка M0 (x0 ;y0 )∈D такая ,что ∫∫f( x, y) dxdy =f (M0)S(D). Свойства: Линейность. ∫∫(α f(x,y)+ β g(x,y) )dxdy= α ∫∫f( x ,y) dxdy+ β ∫∫ g( x, y) dxd Аддитивность. ∫∫ f (x, y) dxdy=∫∫f (x, y) dxdy+∫∫f (x, y) dxdy Интеграл от константы. ∫∫С dxdy=C S(D), если С=const Переход к неравенству. Если для всех точек M ( x,y)∈ D верно неравенство f ( x,y ) ≤ g(x,y), то ∫∫f (x, y) dxdy ≤ ∫∫g(x,y)dxdy
18.Сведение
двойного интеграла к повторному Теорема
1. .
Если функция f(x, y)
интегрируема в прямоугольнике P =
[a, b] [c, d]
и если x [a, b]
существует интеграл ![]() тогда
существует повторный интеграл
тогда
существует повторный интеграл![]() и
он равен двойному:
и
он равен двойному:
![]() Замечание
Если f(x, y)
интегрируема на E и y [c, d]
существует
Замечание
Если f(x, y)
интегрируема на E и y [c, d]
существует ![]() то
он интегрируем по y на
[c, d]
и
то
он интегрируем по y на
[c, d]
и
![]() Теорема 2.
Если функция f(x, y)
интегрируема на E и x [a, b]
существует интеграл
Теорема 2.
Если функция f(x, y)
интегрируема на E и x [a, b]
существует интеграл ![]() то
существует и повторный интеграл
то
существует и повторный интеграл ![]() и
он равен двойному, т.е.
и
он равен двойному, т.е.
![]()
22.Криволинейный
интеграл второго рода и формула его
вычисления. Связь с криволинейным
интегралом первого рода. Определение.Если
сущ. конечные пределы интегральных
сумм
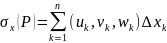 ,
,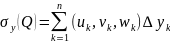 ,
,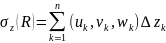 при
при
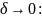
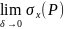 ,
,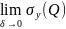 ,
, ,то
эти пределы назыв. криволин. интегралами
2-ого рода по кривой
,то
эти пределы назыв. криволин. интегралами
2-ого рода по кривой
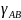 и
соответственно обозначаются
и
соответственно обозначаются
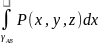 ;
;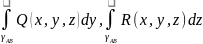 Общий криволинейный
интеграл 2-ого рода обозначают
Общий криволинейный
интеграл 2-ого рода обозначают При смене на кривой
направления кривол. инт. 2-го рода меняет
знак:
=-
При смене на кривой
направления кривол. инт. 2-го рода меняет
знак:
=-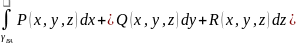 Теорема.
Пусть ф-ции
x(t),y(t),z(t),
входящие в определение кривой
непрерывно
дифференцир. на [a,b],ф-ции
P(x,y,z),
Теорема.
Пусть ф-ции
x(t),y(t),z(t),
входящие в определение кривой
непрерывно
дифференцир. на [a,b],ф-ции
P(x,y,z),
 непрерывны на кривой
,тогда
справедлива формула
непрерывны на кривой
,тогда
справедлива формула
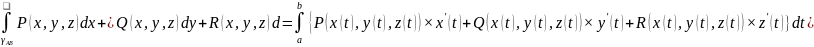 Связь между
кривол. ин. 1-го и 2-го рода.
Пусть (cos
Связь между
кривол. ин. 1-го и 2-го рода.
Пусть (cos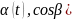 )
есть единичный направляющ. вектор
касательно к кривой
)
есть единичный направляющ. вектор
касательно к кривой

 )dS
)dS
24.Комплексные
числа. Комплексные
числа записываются
в виде: a+
bi. Здесь a
и b
– действительные
числа, а i
– мнимая
единица, т.e. i 2
= –1.
Число a
называется
абсциссой,
a b –
ординатой
комплексного числа a+
bi. Два
комплексных числа a+
bi и a
– bi называются
сопряжёнными
комплексными числами.
![]() Модулем
комплексного
числа называется длина вектора OP..
Модуль комплексного числа a+
bi обозначается
| a+ bi
| или буквой r
и равен:
Модулем
комплексного
числа называется длина вектора OP..
Модуль комплексного числа a+
bi обозначается
| a+ bi
| или буквой r
и равен:
![]() Аргумент
комплексного
числа - это
угол
Аргумент
комплексного
числа - это
угол![]() между
осью OX
и вектором OP,
изображающим это комплексное число.
Тригонометрическая
форма комплексного числа.
Абсциссу a
и ординату b
комплексного
числа a +
bi можно
выразить через его модуль r
и аргумент
между
осью OX
и вектором OP,
изображающим это комплексное число.
Тригонометрическая
форма комплексного числа.
Абсциссу a
и ординату b
комплексного
числа a +
bi можно
выразить через его модуль r
и аргумент
![]() :
:
![]() Рассм.
2 комплексн. числа, запис. в тригонометр.
формуле:
z1 = r1(cos φ1 + i sin φ1)
и z2 = r2(cos φ2 + i sin φ2).
Имеем:
1)
z1+
z2=
r1cos φ1+
r2cos φ2 +i(
r1sin φ1+
r2sin φ2)
Рассм.
2 комплексн. числа, запис. в тригонометр.
формуле:
z1 = r1(cos φ1 + i sin φ1)
и z2 = r2(cos φ2 + i sin φ2).
Имеем:
1)
z1+
z2=
r1cos φ1+
r2cos φ2 +i(
r1sin φ1+
r2sin φ2)
z1* z2= r1r2(cos φ1+ isin φ1 )( cos φ2 + i sin φ2)= r1r2(cos φ1 cos φ2 +i cos φ1 sin φ2+
isin r1r2cos φ2 -sin φ1 sin φ2)= r1r2(cos(φ1+φ2)+isin(φ1+φ2)
|
Из этой формулы след. формула Муавра:
|
![]() .
.
3.
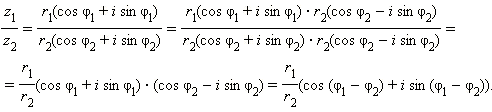
4.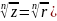 +isin
+isin
 ,k=0,n-1
,k=0,n-1
23.Независимость
криволинейного интеграла от пути
интегрирования. Формула Грина, условие
Эйлера.
Определение.
Криволинейный интеграл II рода называется
независящим
от пути интегрирования,
если результат интегрирования будет
один и тот
же по любому
пути, соединяющему точки A
и B,
на котором функции P
(x;y)
и Q
(x;y)
непрерывны. Обозначение такого интеграла:
 Теорема(формула Грина).пусть
ф-ции P
и Q
имеют в области D
непрерывные частные произ-ые,тогда
инт.
Теорема(формула Грина).пусть
ф-ции P
и Q
имеют в области D
непрерывные частные произ-ые,тогда
инт.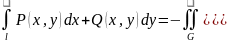 ,при
этом граница в области G
обходится положит. направл-ем.
Формула
Грина исп. для вычисления площадей.
Условие Эйлера
,при
этом граница в области G
обходится положит. направл-ем.
Формула
Грина исп. для вычисления площадей.
Условие Эйлера
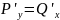 -назыв.
условием Эйлера Теорема.Пусть
односвязное мн-во G
ограничено кривой L,т.е.
кривая L
замкнутая.И пусть ф-ция P
и Q
непрерывно диференц. в области G.Тогда
след. 4 услов. эквивалентны: 1.
-назыв.
условием Эйлера Теорема.Пусть
односвязное мн-во G
ограничено кривой L,т.е.
кривая L
замкнутая.И пусть ф-ция P
и Q
непрерывно диференц. в области G.Тогда
след. 4 услов. эквивалентны: 1.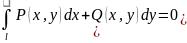 2.Интеграл
2.Интеграл
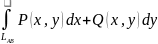 в области G
не зависит от пути интегрирования.
3.Выражение
в области G
не зависит от пути интегрирования.
3.Выражение
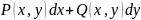 явл. полным дифференц. в области G.
явл. полным дифференц. в области G.
4.Ф-ции P и Q удовлетв. условию Эйлера
Замечание.При
нахождении ф-ции F
за основу можно брать рав-во
 ,котор.
сначало интегрир. по перемен. y,а
затем дифференц. по перем. x.
,котор.
сначало интегрир. по перемен. y,а
затем дифференц. по перем. x.
