
- •1.3. Твердые растворы
- •1.Экстремумы функций. Возрастание и убывание функций.
- •2.Выпуклость, точки перегиба, асимптоты графика функций.
- •3.Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов.
- •4.Замена переменной в неопределенном интеграле. Метод интегрирования по частям.
- •8.Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.
- •5.Определенный интеграл и его геометрический смысл.
- •6.Основные свойства определенного интеграла.
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •14.Производные и дифференциалы высших порядков для функций многих переменных. Формула Тейлора
- •16.Площадь фигуры и объём тела
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
1.3. Твердые растворы
Твердые растворы (ТР) - кристаллические фазы переменного состава, в которых атомы элемента В размещаются в пространственной решетке элемента А, не изменяя ее типа.
Для ТР характерен металлический тип межатомной связи. Твердые растворы обозначают: , , , или А(В). Твердые растворы всегда более тверды, чем чистые металлы, менее пластичны. Их образование всегда сопровождается увеличением электрического сопротивления, как правило, снижаются пластичность и вязкость. Твердые растворы бывают упорядоченными и неупорядоченными. Твердые растворы, устойчивые при сравнительно низких температурах, получили название упорядоченных твердых растворов, или сверхструктур. Полностью упорядоченные растворы образуются в том случае, когда отношение компонентов в сплаве равно целому числу: 1:1, 1:2, 1:3 и т.д. Они занимают промежуточное положение между твердыми растворами и химическими соединениями. При изменении температуры происходит разупорядочение ТР с соответствующим изменением свойств. Температуру разупорядочения к называют точкой Курнакова. Упорядоченные твердые растворы обозначают буквами ’, ’, ’, ’. Все металлы могут в той или иной степени взаимно растворяться друг в друге в твердом состоянии. В тех случаях, когда компоненты могут замещать друг друга в кристаллических решетках в любых количественных соотношениях, образуется непрерывный ряд твердых растворов. Твердые растворы замещения с неограниченной растворимостью могут образоваться при соблюдении следующих условий: 1. Компоненты должны обладать одинаковыми по типу (изоморфными) кристаллическими решетками. 2. Различие в атомных размерах компонентов должно быть не значительным и не превышать 8 – 15 %. 3. Компоненты должны принадлежать к одной и той же группе периодической системы элементов или к смежным родственным группам и в связи с этим иметь близкое строение валентной оболочки электронов в атомах.
1.Экстремумы функций. Возрастание и убывание функций.
Экстре́мум в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)). Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) 0 (f ' (x) 0).
2.Выпуклость, точки перегиба, асимптоты графика функций.
Непрерывная на отрезкеке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
Другими
словами, если для любых
точек x1 и x2 отрезка [a; b] секущая AB проходит
под графиком функции f (x),
то функция f выпукла
вверх. Аналогично определяется функция,
выпуклая вниз. Пусть
функция f (x) непрерывна
в точке х0 и
имеет в этой точке конечную или
бесконечную производную. Тогда
точка х0 называется точкой
перегиба функции f,
если в этой точке изменяется направление
ее выпуклости. Необходимое
условие наличия точки перегиба. Если х0 –
точка перегиба функции f (x),
и функция f (x) имеет
вторую производную, непрерывную в этой
точке, то ![]()
|
Достаточные условия наличия точки перегиба.
Пусть
функция f (x) непрерывна
и имеет конечную или бесконечную
производную в точке ![]() Если
Если ![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку ![]() то
то ![]() –
точка перегиба функции f (x).
–
точка перегиба функции f (x).
асимптоты прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
3.Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов.
Первообра́зной функции f называют
такую F, производная которой
равна f,
то есть F ′
= f.
Вычисление первообразной заключается
в нахождении неопределённого интеграла,
а сам процесс называется интегрированием.
Так, например, функция ![]() является
первообразной
является
первообразной ![]() .
Неопределённый
интегра́л для
функции f(x) —
это совокупность всех первообразных данной
функции.
.
Неопределённый
интегра́л для
функции f(x) —
это совокупность всех первообразных данной
функции.
Если
функция f(x) определена
и непрерывна на промежутке (a,b) и F(x) —
её первообразная, то есть F’(x)=f(x) при a<x<b
, то![]() a<x<b
a<x<b
4.Замена переменной в неопределенном интеграле. Метод интегрирования по частям.
Пусть
функции и(х), v(x) имеют непрерывные
производные, тогда![]() —
формула интегрирования по частям. Она
применяется, если
—
формула интегрирования по частям. Она
применяется, если ![]() более
прост для интегрирования, чем
более
прост для интегрирования, чем ![]() .
для неопределённого
интеграла:
.
для неопределённого
интеграла:
![]() для определённого:
для определённого:
![]()
Пример:
![]()
![]()
![]()
7.Интеграл с
переменным верхним пределом. Формула
Ньютона-Лейбница. Рассмотрим
функцию f(x) ,
заданную на отрезке [a;b] ,
и предположим, что она интегрируема на
отрезке [a;b] .
Тогда при любом ![]() эта
функция будет интегрируема на
отрезке [a;x] и,
следовательно, функция
эта
функция будет интегрируема на
отрезке [a;x] и,
следовательно, функция ![]() определена
при всех
определена
при всех ![]() .
При
.
При ![]() мы
по определению положим её равной 0, то
есть будем считать, что
мы
по определению положим её равной 0, то
есть будем считать, что ![]() для
любой функции f и
точки C из
её области определения. Итак,
функция Ф(х) равняется
значению определённого интеграла с
переменным верхним пределом, вычисленного
от интегрируемой функции f(x) ,
не обязательно непрерывной.
для
любой функции f и
точки C из
её области определения. Итак,
функция Ф(х) равняется
значению определённого интеграла с
переменным верхним пределом, вычисленного
от интегрируемой функции f(x) ,
не обязательно непрерывной.
Формула
Ньютона-Лейбница Пусть
функция f (x) непрерывна
на [a; b],
а F (x) –
какая-либо первообразная функции f на
этом отрезке. Тогда ![]()
|
8.Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.
![]()
![]()
![]()
Доказательство:
![]()
![]()
Так как по формуле интегрирования по частям будет
![]()
![]()
![]() то
то
![]()
![]()
![]()
откуда и следует исходное выражение.
9.Несобственные
интегралы первого и второго рода
Первого
рода.
Предположим, что функция f(x) задана
на бесконечном промежутке вида![]() и
интегрируема на любом конечном
отрезке [a,b] ,
где b>=a .
Таким образом, можно рассмотреть
функцию, зависящую от верхнего предела,
как от переменной:
и
интегрируема на любом конечном
отрезке [a,b] ,
где b>=a .
Таким образом, можно рассмотреть
функцию, зависящую от верхнего предела,
как от переменной:
![]() Если
эта функция имеет предел при
Если
эта функция имеет предел при ![]() ,
то число
,
то число ![]() называется значением
несобственного интеграла первого рода:
называется значением
несобственного интеграла первого рода:
![]() а
сам определенный интеграл
называется сходящимся. Если же
предела не существует, то интеграл
называется расходящимся и не
имеет никакого числового значения.
а
сам определенный интеграл
называется сходящимся. Если же
предела не существует, то интеграл
называется расходящимся и не
имеет никакого числового значения.
5.Определенный интеграл и его геометрический смысл.
Определенный
интеграл —
это аддитивный монотонный нормированный
функционал, заданный на множестве пар,
первая компонента которых — интегрируемая
функция или функционал, а вторая —
область во множестве задания этой
функции. Проще
говоря, это интеграл,
численно равный площади части графика
функции в пределах от a до b,
т. е. площади криволинейной трапеции.
![]() Геометрический
смысл определенного интеграла.
Если f(x)
непрерывна и положительна на [a, b],
то интеграл
Геометрический
смысл определенного интеграла.
Если f(x)
непрерывна и положительна на [a, b],
то интеграл![]()
![]() представляет
собой площадь криволинейной трапеции,
ограниченной линиями y =
0, x = a, x = b, y = f(x).
представляет
собой площадь криволинейной трапеции,
ограниченной линиями y =
0, x = a, x = b, y = f(x).

6.Основные свойства определенного интеграла.
-Величина
определенного интеграла не зависит от
обозначения переменной интегрирования,
т.е. ![]() ,
где х, t – любые буквы.
,
где х, t – любые буквы.
-Определенный
интеграл с одинаковыми пределами
интегрирования равен нулю.
![]()
-При
перестановке пределов интегрирования
определенный интеграл меняет свой знак
на обратный.
![]()
-Постоянный
множитель можно выносить за знак
определенного интеграла.
![]()
-интеграл
суммы равен сумме ингералов![]()
10.Векторное
пространство
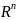 :
основные понятия
:
основные понятия
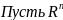 – множество возможных упорядоченных
после-ей n
действительных чисел. Элементы
x=(x1,x2…xn)
множество
будем называть точками, а точки
x1…xn-координатами.
Суммой наз-ся точка x+y=(x1+y1…xn+yn),
произведение ax=(ax1…axn).Расстоянием
в
называют
функцию d
: (x,y)
– множество возможных упорядоченных
после-ей n
действительных чисел. Элементы
x=(x1,x2…xn)
множество
будем называть точками, а точки
x1…xn-координатами.
Суммой наз-ся точка x+y=(x1+y1…xn+yn),
произведение ax=(ax1…axn).Расстоянием
в
называют
функцию d
: (x,y)
![]()
 →
d(x,y)
→
d(x,y)![]() R
удовлетворяющую условиям:
R
удовлетворяющую условиям:
d(x; y) > 0; d(x; y) = 0
 x = y
x = yd(x; y) = d(y; x) (симметричность)
d(x; y) < d(x; z) + d(z; y) (неравенство треугольника)
Формула
d(x,y)=
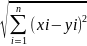 –определяет расстояние в
–определяет расстояние в
Точка m наз-ся граничной точкой множества M, если в любой её окружности есть точка множества М и точки не принадлежат М. Совокупность всех граничных точек мно-ва М наз-ся границей М.
12.Непрерывность
функции многих переменных
Определение1.Функция
f
наз. непрерывной в точке x0,
если lim
f(x)=f(x0).
Это означает, что
(![]() ε
> 0
ε
> 0![]() δ
> 0) (
x
D,
d(x,x0)<
δ): d (f (x), f (x0))
< ε.
Определение
2. Функция
y=f(x)
непрерывна в точке x0
вдоль множества L,
если lim
f(x)=f(x0)
при x→x0
Определение3.
Функция u
= f(x)
= f(x1
… xn)
называется непрерывной в точке a
= (a1…
an)
по переменной xk
, если lim при Δxk → 0 δxku = 0.
Теорема
1. Если функция
u = f(x) = f(x1, x2, … , xn) непрерывна в точке
a, то она непрерывна в этой точке по
каждой переменной x1, x2, … , xn .
Обратное
утверждение неверно.
Теорема
2. Пусть
функции f(x) и g(x) , определены в области
D М Rn и непрерывны в точке a = (a1, a2, … ,
an)
D . Тогда
функции f(x) + g(x) , f(x) · g(x) и f(x)/g(x) (при g(a)
≠ 0) непрерывны в точке а Теорема
3. Всякая
элементарная функция нескольких
переменных непрерывна на множестве,
на котором она определена. Теорема
4. Функция,
непрерывная на замкнутом ограниченном
множестве, ограничена на этом множестве.
Теорема
5 (Вейерштрасс).
Функция, непрерывная на замкнутом
ограниченном множестве, достигает на
этом множестве своего наибольшего и
наименьшего значений.
δ
> 0) (
x
D,
d(x,x0)<
δ): d (f (x), f (x0))
< ε.
Определение
2. Функция
y=f(x)
непрерывна в точке x0
вдоль множества L,
если lim
f(x)=f(x0)
при x→x0
Определение3.
Функция u
= f(x)
= f(x1
… xn)
называется непрерывной в точке a
= (a1…
an)
по переменной xk
, если lim при Δxk → 0 δxku = 0.
Теорема
1. Если функция
u = f(x) = f(x1, x2, … , xn) непрерывна в точке
a, то она непрерывна в этой точке по
каждой переменной x1, x2, … , xn .
Обратное
утверждение неверно.
Теорема
2. Пусть
функции f(x) и g(x) , определены в области
D М Rn и непрерывны в точке a = (a1, a2, … ,
an)
D . Тогда
функции f(x) + g(x) , f(x) · g(x) и f(x)/g(x) (при g(a)
≠ 0) непрерывны в точке а Теорема
3. Всякая
элементарная функция нескольких
переменных непрерывна на множестве,
на котором она определена. Теорема
4. Функция,
непрерывная на замкнутом ограниченном
множестве, ограничена на этом множестве.
Теорема
5 (Вейерштрасс).
Функция, непрерывная на замкнутом
ограниченном множестве, достигает на
этом множестве своего наибольшего и
наименьшего значений.
11.Предел
последовательности в IRn.
Предел функции
многих переменных. Отображение
a
: N ,
a
: k
а(k)
=
,
a
: k
а(k)
= (
(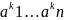 ),
наз-ся послед-ью точек из
.
Последовательность
обозначают (
),
наз-ся послед-ью точек из
.
Последовательность
обозначают (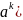 .
Говорят,что после-ть(
)
сход-ся к пределу а
,
если lim при
k
.
Говорят,что после-ть(
)
сход-ся к пределу а
,
если lim при
k d(
,a)=0
Теорема.
lim
при k
d(
,a)=0
Теорема.
lim
при k
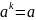 =(a1…an)
lim
при k
=(a1…an)
lim
при k
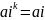 ,
i=1,..n
Док-во:
Пусть lim
при k
,
i=1,..n
Док-во:
Пусть lim
при k
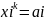 ,
т.е при достаточно больших k
выпол.
,
т.е при достаточно больших k
выпол.
 ,
тогда g(
,
тогда g( .
Теорема доказана.
Теорема(критерий
Коши): Для того,ч тобы пос-ть сходилась
необходимо и достаточно, чтобы она была
фундаментальной:
.
Теорема доказана.
Теорема(критерий
Коши): Для того,ч тобы пос-ть сходилась
необходимо и достаточно, чтобы она была
фундаментальной:
 Число А
Число А
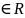 наз-ся пределом фу-ции u=f(x)
при x
наз-ся пределом фу-ции u=f(x)
при x ,
если
,
если
 .
.
Пусть
L
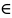 X,
a-
предельная точка множества L.
Число А наз-ют пределом ф-ции f
при х
X,
a-
предельная точка множества L.
Число А наз-ют пределом ф-ции f
при х ,
если
,
если
если
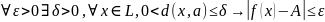 и обозначают lim
при х
,
х
и обозначают lim
при х
,
х f(x)=A.
f(x)=A.
