13. Толщина вытеснения, потери импульса и энергии

Для расчета потерь массы, импульса и энергии в пограничном слое вводятся следующие интегральные величины:

Толщина вытеснения.

Разность масс жидкости, протекающих в основном потоке и в пограничном слое, составит (₀ u₀ -  u(y) ) dy

Для всего слоя

Разделив этот интеграл на 0 u0 , получим толщину вытеснения

Толщина потери импульса основного потока в пограничном слое.

Масса жидкости  u(y) dy теряет в пограничном слое количество движения, равное u (u₀ - u(y)). Для всего слоя эта потеря составит

Разделив интеграл на ₀ u₀², получим толщину потери импульса

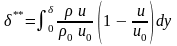
Толщина потери энергии основного потока в пограничном слое.

Масса жидкости  u(y) dy теряет в пограничном слое кинетическую энергию, равнуюu (u₀² - u²(y)). Для всего слоя эта потеря составит

. Разделив интеграл на 0 u0³ , получим толщину потери энергии

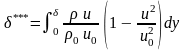
Под расчетом пограничного слоя понимается определение распределения *, **, *** вдоль обтекаемой поверхности.

14. Вывод уравнения Кармана и его анализ

получим уравнение Кармана

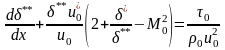
Правая часть уравнения представляет коэффициент трения Cf, который может быть представлен в следующем виде:

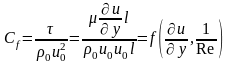
Целью проектирования любого аэродинамического устройства является минимизация потерь, т.е. **min. Поскольку 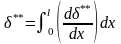, то чем больше степень нарастания толщины потери импульса, тем больше потери, равные ₀ u₀ ²**. Определяющим потери фактором является продольный градиент изменения скорости основного потока (u`<sub>o</sub>) или градиент давления dp/dx. При отрицательном градиенте скорости (u`_o<0, dp/dx>0) происходит быстрое нарастание **, которое в свою очередь приводит к увеличению числа и более раннему переходу (Re** > Re**_кр) ламинарного режима течения в турбулентный в пограничном слое. Это в свою очередь сопровождается изменением профиля скорости в пограничном слое так, что

В результате увеличивается коэффициент трения Сf, что еще больше увеличивает d**/dx и, соответственно, ** несмотря на то, что отношение */** уменьшается при переходе от ламинарного к турбулентному режиму течения.

16. Уравнение движения газа для турбулентного течения

При турбулентном течении ( Re>10⁴) скорость и давление в фиксированной точке пространства не остаются постоянными во времени, а изменяются случайным образом. Такие изменения называются пульсациями. Элементы жидкости, пульсирующие как целое вдоль и поперек основного течения, представляют собой не отдельные молекулы (как в ламинарном течении), а макроскопические образования.

Движение частицы в этом случае представляется в виде суммы средней скорости (давления) и пульсационной составляющей (со штрихом)

. ,

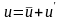Фундаментальным свойством турбулентного течения является влияние пульсационных составляющих скорости (u`) на осредненное движение (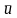 ) так, что в осредненном движении как бы увеличивается вязкость осредненного движения (“кажущаяся вязкость”), т.е. появляются дополнительные касательные напряжения.

Система уравнений, описывающая двумерное нестационарное турбулентное течение в пограничном слое, может быть записана в следующем виде:

Уравнение неразрывности:

Уравнение движения в направлении Х:

Уравнение энергии:

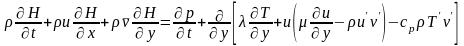
Уравнение состояния:

Модель турбулентности, связывающая касательные напряжения Рейнольдса с градиентом составляющей средней скорости через турбулентную вязкость:

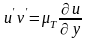
Модель турбулентного теплового потока:

Решение этой системы уравнений в частных производных производится численными методами. В результате, мы получаем распределение всех параметров жидкости (газа) по двум координатам в различные моменты времени. В частности, на стенке мы можем определить и градиент температуры и, следовательно, по закону Фурье найти тепловой поток.

Как следует из этих уравнений, распределение теплосодержания поперек толщины пограничного слоя зависит от турбулентности потока (величины пульсаций скорости). Интуитивно очевидно, что в турбулентном пограничном слое градиент температуры потока вблизи стенки будет выше, чем в ламинарном, за счет более интенсивного переноса энергии поперек потока с помощью пульсаций. Отсюда и тепловой поток также будет больше. Следовательно, в отличие от твердых тел, коэффициент пропорциональности теплового потока градиенту между средней температурой жидкости и стенки зависит не только от физических свойств теплопроводящей среды ( ), но и от режима обтекания. В этом случае этот коэффициент пропорциональности носит название коэффициента теплоотдачи (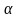 ).