1 .2 Если для молекулы возможны две или более ориентации в пространстве, неотличимые друг от друга, молекула обладает симметрией. Действительно, оба атома водорода совершенно неразличимы, обе ориентации эквивалентны, и молекула обладает симметрией. Ориентации можно получить путем вращения молекулы на 180° вокруг оси, проходящей через центр молекулы и перпендикулярной линии связи водород-водород. Такое вращение называется операцией симметрии, а ось вращения - элементом симметрии. Элементом симметрии может быть линия, точка или плоскость, относительно которых совершается операция симметрии.

Точечная симметрия включает набор операций, преобразующих систему с сохранением некоторой точки, которой обычно является центр тяжести молекулы.

Э лементы симметрии. Существует пять типов элементов симметрии, которые нужно рассматривать при точечной симметрии: 1) центр симметрии (центр инверсии), 2) ось вращения, 3) плоскость отражения, 4) ось вращения с отражением и 5) идентичность.

Ц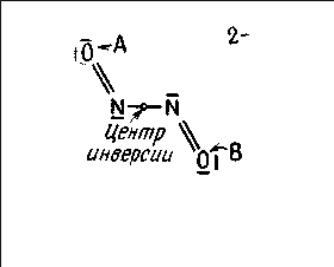 ентр симметрии, или центр инверсии. Молекула обладает центром симметрии, если отражение каждого из атомов через этот центр приводит к совпадению с другим идентичным атомом. Если в гипонитрит-ионе атом кислорода А передвинуть через центр инверсии на такое же расстояние на противоположной стороне от центра, он совпадет с другим атомом кислорода. То же относится к атому В и к обоим атомам азота. При этом молекула обладает центром симметрии. Другими примерами молекул или ионов, которые, как легко показать, имеют центр симметрии, являются 1,4-диоксан, Ni(CN)₄^2-, транс-дихлорэтилен и транс-дихлортетрамминко-бальт(Ш). При такой операции все точки в молекуле, обладающей центром симметрии, должны быть способны инвертироваться одновременно. Только при выполнении этого условия молекула как целое имеет этот элемент симметрии. Центр инверсии (центр симметрии) обозначается символом i.

Ось вращения. Если в молекуле можно провести воображаемую ось, вращение вокруг которой приводит к эквивалентной ориентации, то говорят, что такая молекула обладает осью вращения. Этот элемент часто называется собственной осью вращения. Вокруг одной оси вращения можно провести различные операции симметрии. Если при вращении вокруг оси молекула может принимать n различных эквивалентных положений, ось называется осью n-го порядка. Рассмотрим, например, ось, проходящую через центральный атом бора в молекуле ВС1₃ перпендикулярно плоскости молекулы. Двухкратное вращение вокруг этой оси каждый раз на угол 120° приводит к двум эквивалентным ориентациям. Если добавить еще исходную ориентацию, мы будем иметь три различные эквивалентные ориентации. При этом говорят, что молекула имеет ось вращения третьего порядка, обозначаемую символом С₃. Очевидно, что ось, проходящая через центр молекулы бензола и перпендикулярная плоскости кольца, является осью шестого порядка С₆. Дальнейшее рассмотрение молекулы ВС1₃ указывает на отсутствие центра симметрии и наличие еще трех осей второго порядка С₂. Ось вращения высшего порядка называется главной осью и обозначается Сn. Если у молекулы имеется несколько осей Сn (высшего порядка), то главную ось нужно выбрать коллинеарной с какой-то одной осью молекулы. Если все Сn эквивалентны, то любая из них может быть выбрана в качестве главной. При n=1 молекулу для получения эквивалентной ориентации (в этом случае единственной) нужно повернуть на 360°. При этом говорят, что молекула вообще не имеет симметрии (если нет каких-либо других элементов симметрии). Для молекулы водорода n=∞.

П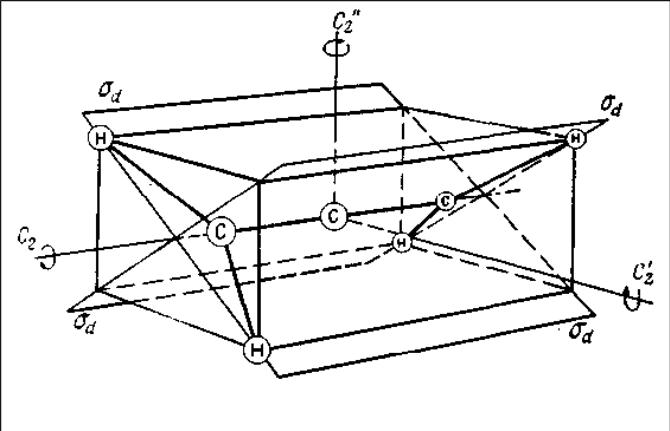 лоскости симметрии, или плоскости отражения. Если в молекуле имеется плоскость, разделяющая молекулу на две половины, каждая из которых является зеркальным отображением другой, то молекула обладает элементом симметрии - плоскостью отражения. Эта плоскость не может находиться вне молекулы и должна проходить через нее. В плоскости отражения могут располагаться многие оси симметрии, но известны и примеры, когда плоскость отражения не содержит осей симметрии. Примером, иллюстрирующим Такое положение, может служить тетраэдрическая молекула РОВг₂Сl. У этой молекулы нет осей вращения, но имеется плоскость отражения, в которой расположены атомы Р, С1 и О. Наличие плоскости симметрии обозначается символом σ. Если у молекулы, как, например, у ВС1₃, имеется более одной плоскости симметрии, то горизонтальной плоскостью σ_h, считается плоскость, перпендикулярная главной оси (оси вращения высшего порядка). На рис. плоскостью σ_h является плоскость самой молекулы ВС1₃, и, кроме того, имеются еще три вертикальные плоскости σ_v.

В некоторых молекулах плоскости отражения содержат главную ось, но ни одной из перпендикулярных ей осей С₂. Такие плоскости являются биссектрисами углов между двумя осями С₂ (в плоскости ху) и называются диэдрическими плоскостями (сокращенно σ_d).

Идентичность. При операции идентичности в молекуле не происходит никаких изменений. Очевидно, что результатом этой операции является появление не просто эквивалентной ориентации, а совершенно идентичной, т. е. если пометить одинаковые атомы одним, двумя и более штрихами, то после операции ничего не изменится. Этот элемент симметрии имеется у всех молекул; он обозначается символом Е. Введение операции идентичности необходимо для того, чтобы рассматривать элементы симметрии с помощью соответствующего раздела математики.

3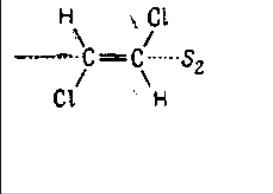 .4 Операция вращения-отражения включает вращение вокруг оси, за которым следует зеркальное отражение в плоскости, перпендикулярной оси. Результат этих двух операций должен приводить к эквивалентной конфигурации. Эти операции также называются несобственными вращениями, а соответствующие оси - зеркально-поворотными осями. Для обозначения этого элемента симметрии используется символ S. Такая ось в молекуле транс-дихлорэтилена изображена пунктирной линией. Индекс 2 указывает, что это ось второго порядка, т. е. соответствует вращению на 180°. Следует отметить, что в действительности ось S2 эквивалентна i и часто обозначается символом i. Несобственные оси высших порядков обозначаются Sn.

На рис. изображена некоторая ориентация молекулы метана. Светлые кружки и квадратики обозначают атомы водорода, находящиеся в плоскости, параллельной плоскости чертежа и расположенной выше нее, а черные кружки и квадратики - атомы в плоскости ниже плоскости чертежа. Плоскость чертежа является плоскостью отражения, и в ней находится атом углерода. Операция С4 ясна сама собой. Операция отражения σ переводит атомы водорода под плоскостью чертежа в атомы над этой плоскостью и обратно. Это показано путем замены черных квадратов на светлые и светлых кружков на черные. Но, поскольку все четыре атома водорода идентичны, исходная и окончательная ориентации эквивалентны. У молекулы имеется зеркально-поворотная ось четвертого порядка S4. Эту операцию можно повторить еще три раза, т. е. всего четыре раза. S4 эквивалентно операции С2 вокруг той же оси. Молекула имеет еще две другие зеркально-поворотные оси, и эти элементы симметрии обозначаются сокращенно символами S' и S". Операция S4 эквивалентна вращению на 90° против часовой стрелки с последующим отражением.

5 Все молекулы можно классифицировать по точечным группам, к которым они относятся. Каждая точечная группа представляет собой набор всех операций симметрии, которые могут быть произведены с молекулой, принадлежащей к этой группе.

Молекула, относящаяся к точечной группе Сn, имеет только один элемент симметрии - ось вращения n-го порядка. (не учитывая Е) Такая молекула, как транс-дихлорэтилен, у которой есть горизонтальная плоскость отражения, перпендикулярная ее оси вращения Сn, относится к точечной группе Cnh. Точечная группа Cnv включает такие молекулы, как вода и сульфурилхлорид, у которых имеется n вертикальных плоскостей отражения, содержащих оси вращения, но нет горизонтальных плоскостей отражения. Молекулы Н20 и SO2C12, относящиеся к группе C2v, имеют только одну ось вращения и две плоскости σv.

Для точечных групп, которые включают, помимо оси Сn еще n осей С2, перпендикулярных Сn используется символ Dn. Точечная группа Dn соответствует более высокой симметрии, чем группа Сn. Молекула, обладающая всеми элементами симметрии точечной группы Dn и имеющая сверх того горизонтальную плоскость отражения, перпендикулярную оси Сn относится к точечной группе Dnh и имеет n вертикальных плоскостей отражения. Примером молекулы, относящейся к точечной группе D3h, является ВС13. В точечных группах Dnh плоскости σh, перпендикулярные главной оси, содержат все оси С2 и каждая плоскость σv содержит главную ось и одну из осей С2.

Молекулы Dn могут иметь также плоскости σd, которые включают главную ось Сn, но ни одной из перпендикулярных осей С2. Обозначением для молекул Dn, содержащих этот элемент симметрии σd, является символ Dnd. Такая молекула имеет ось n-го порядка, n осей второго порядка С2, перпендикулярных Сn, и, кроме того, n (вертикальных) плоскостей симметрии, рассекающих пополам углы между двумя осями второго порядка и включающими ось Сn. Примером молекулы, относящейся к точечной группе D2d, является аллен Н2С = С = СН2.

К кубическим относятся точечные группы, имеющие более чем одну ось порядка выше двух. К ним относятся точечные группы правильных тетраэдра (Td), октаэдра и куба (Oh).

6 Большое влияние на полярность молекулы оказывает ее симметрия. Если молекула имеет высокосимметричное строение, то она не полярна. И наоборот молекулы, которые характеризуются асимметрией – полярны. Например, молекула метана CH4 обладает высокой степенью симметрии (центрированный тетраэдр), и поэтому векторная сумма дипольных моментов связей (m=0,4D) равна нулю. Если заменить водородные атомы на атомы хлора и получить молекулу CCl4, у которой дипольный момент связи m=2,05D, то есть в пять раз больший, чем для CH4, то результат останется прежним, так как молекула CCl4 обладает таким же строением.

Полярными называются молекулы, обладающие ненулевым дипольным моментом. Следовательно, полярными могут быть только молекулы с симметрией Сn или Cnv. Таким образом, точечная группа показывает, может ли данная молекула обладать дипольным моментом, и если да, то обычно известно и направление вектора m (иногда остается неопределенным лишь его знак). Здесь мы сталкиваемся с характерной ситуацией. Симметрия молекулы указывает на возможность существования дипольного момента и дает более или менее определенные сведения о его направлении. Во многих случаях она позволяет дать отрицательный ответ на вопрос о полярности молекулы. Но вместе с тем симметрия сама по себе никогда не дает оснований утверждать, что молекула должна обладать сколько-нибудь значительным, экспериментально фиксируемым дипольным моментом. Количественные характеристики вектора m зависят от природы молекулы, от ее состава и строения. С аналогичным соотношением между симметрией молекулы (или кристалла) и свойствами нередко приходится встречаться и в других случаях.

7 Оптическая активность связана лишь с определенным видом

диcсимметрии , а именно с дисcимметрией, обусловливающей несовместимость объекта с его зеркальным отображением. Такой вид диссимметрии получил название хиральность. Хиральные объекты относятся друг к другу как правая и левая рука, или винты с правой и левой резьбой, т.е. они несовместимы в пространстве и представляются как зеркальные отображения друг друга. Оптически активная молекула хиральна, а оптически неактивная ахиральна, однако если молекулу нельзя совместить с ее зеркальным отображением, то зеркальное отображение соответствует другой, отличной молекуле, которую, в принципе, можно синтезировать. Синтезированное зеркальное отображение хиральной молекулы будет ее реальным оптическим изомером. Чистое оптически активное соединение имеет два и только два оптических изомера (т.к. каждому объекту соответствует лишь одно зеркальное отображение).

Х иральностью принято называть способность фигуры не совмещаться со своим зеркальным отображением. Фигуры, обладающие таким свойством, называются хиральными, а не обладающие им — ахиральными. Две фигуры, которые можно совместить с помощью поворотов и поступательных перемещений в пространстве, называются тождественно равными. Если такое совмещение осуществимо только после отражения одной из фигур в плоскости (или инверсии в точке), то фигуры называются зеркально равными (или энантиомерными). Хиральные фигуры существуют в виде двух зеркально равных форм — энантиомеров; если один из энантиомеров назвать «правым», то второй будет «левым». В случае ахиральных фигур нет различия между зеркальным и тождественным равенством. Хиральность или ахиральность непериодической фигуры непосредственно связана с ее точечной группой симметрии. Если группа содержит какую-либо инверсионную ось (в том числе центр инверсии или плоскость симметрии), фигура ахиральна. В противном случае она обладает хиральностью.

8 В приближённых подходах квантовой химии, использующих

представление о молекулярных орбиталях, классификация по симметрии возможна не только для волновой функции молекулы в целом, но и для отдельных орбиталей. Если у равновесной конфигурации молекулы имеется плоскость симметрии, в которой лежат ядра, то все орбитали этой молекулы разбиваются на два класса: симметричные (s) и антисимметричные (p) относительно операции отражения в этой плоскости. Молекулы, у которых верхними (по энергии) занятыми орбиталями являются p-орбитали, образуют специфические классы ненасыщенных и сопряжённых соединений с характерными для них свойствами. Знание локальной симметрии отдельных фрагментов молекул и локализованных на этих фрагментах молекулярных орбиталей позволяет судить о том, какие фрагменты легче подвергаются возбуждению и сильнее меняются в ходе химических превращений, например при фотохимических реакциях.

9 Теория групп является разделом математики, который

применяется к некоторым задачам, удовлетворяющим определенным требованиям. Есть много проблем, представляющих интерес для химика, к которым можно подойти с помощью этого метода. Сюда относятся: описание молекулярных колебаний, классификация молекулярных электронных орбиталей, вывод правил отбора для переходов в инфракрасных спектрах и спектрах комбинационного рассеяния и электронных переходов, составление гибридных и молекулярных орбиталей, вывод расщеплений в кристаллическом поле и многочисленные другие применения

Для того чтобы набор элементов составлял группу (т. е. образование, подчиненное правилам теории групп), должны быть удовлетворены определенные условия. Эти условия являются довольно общими, но их смысл более целесообразно проиллюстрировать на простом примере элементов симметрии молекулы воды, которая принадлежит к точечной группе С2с, включающей операции симметрии Е, С2, σv и σ'v:

1. Произведение любых двух операций, входящих в группу, или квадрат какой-либо операции должны представлять собой также операцию, входящую в данную группу. По условию ось высшего порядка принимается за ось. z. В данном случае точечной группы C2v такой осью является С2, а три атома молекулы воды определяют плоскость уz, являющуюся плоскостью отражения σ'v. Перемножение двух операций означает последовательное применение этих операций симметрии. Таким образом, произведение С2 x σv= σv. Вместо термина «произведение» для этой операции можно использовать более точный термин «комбинация». Возведение всех операций симметрии в квадрат и рассмотрение всех комбинаций показывает, что результатом этих комбинаций всегда является другой элемент точечной группы C2v. Некоторые комбинации зависят от порядка произведения операций..

2. Одна операция в группе должна коммутировать со всеми остальными операциями и оставлять их без изменения. Такая операция называется идентичностью и обозначается сокращенно символом Е.

3. Для комбинаций должен выполняться закон ассоциативности. Результат комбинации трех операций должен быть одинаковым в случаях, когда первый элемент комбинируется с произведением двух остальных, т. е. σv(C2σv), и когда произведение двух первых комбинируется с последним из элементов, т. е. (σvC2) σv’.

4. Каждому элементу должен соответствовать обратный элемент, который также является элементом группы. Это требование означает, что для каждой операции симметрии должна существовать другая операция, ликвидирующая результат действия первой операции. Для каждой плоскости отражения обратным элементом является идентичная плоскость отражения, т. е. σ x σ = Е.

Поскольку операции симметрии удовлетворяют требованиям теории групп, к точечным группам можно подходить с помощью теоретико-групповых методов.

Для интерпретации спектральных данных большое значение имеют свойства симметрии переходов или движений в молекуле. Результаты воздействия операций симметрии на различные свойства молекулы, относящейся к данной точечной группе, могут быть суммированы с помощью таблицы характеров этой группы.

Таблицы характеров строятся на основании законов теориигрупп.

Д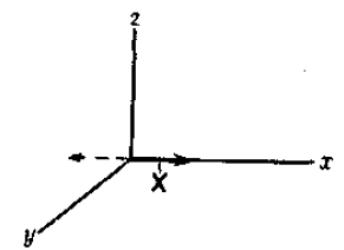 ля того чтобы продемонстрировать ее использование, рассмотрим влияние операций симметрии точечной группы C2v на единичный вектор X, расположенный вдоль оси х в системе координат х, у, z, где ось z — главная ось молекулы. Компоненты у и z этого вектора равны нулю для всех операций группы, так что мы можем преобразовывать X независимо от у и z. Операция идентичности Е не изменяет координат, и мы указываем это с помощью коэффициента +1. Эта величина называется характером операции Е, совершаемой над X. Как показано с помощью пунктирной стрелки на рис, операция С2 изменяет компоненту х вектора X, превращая ее в -х, так что характер операции С2, совершаемой над X, можно представить как —1. Операции σv и σ'v, совершаемые над X имеют характеры +1 и —1 соответственно. С помощью таблицы характеров мы можем установить, что результаты ( + 1, — 1, +1 и —1) соответствуют строке, обозначенной символом B1. Можно сказать, что вектор X преобразуется под действием операций симметрии группы C2v по типу B1. Эти типы называются неприводимыми представлениями точечной группы. Если применить такой же набор операций, которые были описаны выше для вектора вдоль оси х к векторам Y и Z, направленным соответственно вдоль осей у и z, мы увидим, что они преобразуются как типы А1 и В2. Символы R обозначают вращения. Возможны три вращения (вокруг осей х, у и z) Rx, Ry и Rz. Для того чтобы показать, как преобразуются вращения, поместим круглую стрелку в начало системы координат вокруг оси, указанной в нижнем индексе, например для Rz при г=0 и вокруг оси г. Хотя это и несущественно для наших целей, но принято располагать ее так, чтобы она была повернута по часовой стрелке для наблюдателя. находящегося в начале координат и смотрящего вдоль оси. Если над такой стрелкой производятся операции симметрии и при этом ее направление не изменяется, то характер равен +1, а если изменяется, то характер равен —1. Можно без труда увидеть, что Rx, Ry и Rz преобразуются соответственно как типы симметрии В2, В1 и А2. Рассмотрим теперь точку в системе координат, изображенной на рис. у которой все координаты х, у и z положительные. Операция Е оставляет координаты точки неизменными, и сумма коэффициентов перед координатами х, у и z равна 3. В этом примере характером является сумма коэффициентов, т. е. +3. Если стрелка расположена вдоль оси х, сумма коэффициентов для нее равна +1, так как коэффициенты перед у и z равны 0. Операция С2 преобразует координаты х, у и z в —х, —у и z. Характер для этой операции, равный сумме коэффициентов —1, —1 и +1, составляет —1. Операция σV(xz) приводит к х, —y, z, т. е. имеет характер +1, а операция σ'v(yz) приводит к —х, +у, +z, т. е. имеет характер +1. Полное, так называемое приводимое представление этих операций можно записать в виде >> где Г — общий символ для обозначения представления, если тип симметрии не известен. Приводимое представление может быть разложено на сумму неприводимых представлений. В нашем примере оно соответствует сумме типов А1, B1 и В2 >>>

Неприводимые представления в таблице характеров (т. е. А1, А2, В1 и В2) не могут быть разложены далее. Поскольку точка, которую мы рассматривали в начале этого абзаца, имеет координаты х, у и z, можно ожидать, что для нее приводимое представление будет состоять из суммы неприводимых представлений для векторов X, Y и Z. В рассмотренном выше примере неприводимые представления, составляющие приводимое представление, могут быть легко найдены путем сложения различных возможных комбинаций неприводимых представлений до тех пор, пока не будет получен правильный результат. В последнем правом столбце табл. указаны типы симметрии для квадратов и двойных произведений координат х, у и z. Прямое произведение двух векторов получается путем умножения неприводимых представлений для каждого из них, например XY = B1xB2 = A2. При этом умножении используются следующие факты: Результат ( + 1, +1, —1, —1) идентичен с неприводимым представлением А2; следовательно, B1xB2=A2- Когда симметрия молекулы установлена, соответствующая таблица характеров позволяет разобраться во многих свойствах молекулы.