Метод наименьших квадратов (мнк)
Метод нахождения оценки неизвестного параметра Ө, основанный на минимизации суммы квадратов отклонений выборочных данных от искомой оценки Ө. Другими словами, в МНК требуется найти такое значение , которое минимизировало бы сумму
Выполнение работы.
1)Проверка гипотезы о виде закона распределения (по критерию хи-квадрат).
Вариационный ряд выборки:
-3,665 |
-3,289 |
-3,064 |
-2,936 |
-2,891 |
-2.846 |
-2,728 |
-2,590 |
-2,572 |
-2,570 |
-2,530 |
-2,502 |
-2,480 |
-2,447 |
-2,414 |
-2,356 |
-2,222 |
-2,150 |
-2,055 |
-2,039 |
-2,013 |
-1,948 |
-1,930 |
-1,899 |
-1,883 |
-1,865 |
-1,820 |
-1,767 |
-1,753 |
-1,707 |
-1,696 |
-1,670 |
-1,667 |
-1,632 |
-1,620 |
-1,605 |
-1,587 |
-1,584 |
-1,558 |
-1,503 |
-1,491 |
-1,489 |
-1,488 |
-1,487 |
-1,473 |
-1,447 |
-1,428 |
-1,366 |
-1,365 |
-1,351 |
-1,338 |
-1,295 |
-1,287 |
-1,264 |
-1,252 |
-1,227 |
-1,212 |
-1,185 |
-1,181 |
-1,170 |
-1,128 |
-1,124 |
-1,076 |
-1,066 |
-1,059 |
-1,022 |
-1,010 |
-1,000 |
-0,970 |
-0,938 |
-0,907 |
-0,891 |
-0,890 |
-0,869 |
-0,808 |
-0,774 |
-0,745 |
-0,738 |
-0,712 |
-0,708 |
-0,677 |
-0,673 |
-0,579 |
-0,566 |
-0,557 |
-0,551 |
-0,550 |
-0,483 |
-0,464 |
-0,448 |
-0,371 |
-0,339 |
-0,320 |
-0,145 |
-0,020 |
-0,053 |
0,059 |
0,089 |
0,090 |
0,719 |
Оценка математического ожидания: -1,380
Оценка дисперсии: 0,679
Оценка среднего квадратического отклонения: 0,824
Разобьем
вариационный ряд выборки на
полуинтервалов.
[-3,665; -2,570]
(-2,570; -2,039]
(-2,039; -1,707]
(-1,707; -1,503]
(-1,503; -1,351]
(-1,351; -1,170]
(-1,170; -0,938]
(-0,938; -0,708]
(-0,708; -0,448]
(-0,448; 0,719]
Вычислим
гипотетические вероятности
попадания
в полуинтервалы.
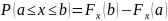
Результаты вычислений сведем в таблицу
Интервал |
|
[-3,665; -2,570] |
0,072 |
(-2,570; -2,039] |
0,137 |
(-2,039; -1,707] |
0,130 |
(-1,707; -1,503] |
0,096 |
(-1,503; -1,351] |
0,076 |
(-1,351; -1,170] |
0,080 |
(-1,170; -0,938] |
0,110 |
(-0,938; -0,708] |
0.120 |
(-0,708; -0,448] |
0,080 |
(-0,448; 0,719] |
0,120 |
Вероятность
попадания в интервал (-
,-3,665)
равна
,
а в
интервал
(0,719; +
)
Вычислим реализацию статистики критерия хи-квадрат по формуле
Вспомогательная таблица для вычислений
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1,070 |
0,999 |
0,692 |
0,017 |
0,758 |
0,5 |
0,091 |
0,333 |
0,5 |
0,333 |
Тогда
При
справедливости гипотезы о нормальном
распределении статистика Z имеет
распределение
.Тогда
критическая область
имеет
вид
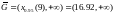,а
доверительная область-
.
Так как вычисленное по выборке значение статистики попадает в доверительную область, то с вероятностью 0,95 можно утверждать, что данные выборки согласуются с гипотезой о нормальном распределении.
Теперь проверим гипотезу о том что выборка имеет равномерное распределение. Разбиение на полуинтервалы , количество элементов, попавших в каждый из них, математическое ожидание и дисперсия не изменятся.
Равномерное
распределение
имеет
два независимых параметра:
и
. Найдем их из системы:
;
Вычислим
вероятности
попадания в интервалы по формуле:
Результаты вычислений сведем в таблицу
Интервал |
|
[-3,665; -2,570] |
0,384 |
(-2,570; -2,039] |
0,186 |
(-2,039; -1,707] |
0,116 |
(-1,707; -1,503] |
0,072 |
(-1,503; -1,351] |
0,053 |
(-1,351; -1,170] |
0,064 |
(-1,170; -0,938] |
0,081 |
(-0,938; -0,708] |
0,080 |
(-0,708; -0,448] |
0,092 |
(-0,448; 0,719] |
0,408 |
Вероятность
попадания в полуинтервалы (-
,-2,9443),
равна
нулю.
Вычислим статистику реализации хи-квадрат по формуле
Вспомогательная таблица для вычислений
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
21,004 |
3,976 |
0,221 |
1,089 |
4,168 |
2,025 |
0,446 |
0,5 |
0,07 |
23,251 |
Тогда
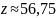
Так как вычисленное по выборке значение статистики не попадает в доверительную область, вычисленную ранее, то с вероятностью 0,95 можно утверждать, что данные выборки не согласуются с гипотезой о равномерном распределении.
Теперь проверим гипотезу о том что выборка имеет экспоненциальное распределение. Разбиение на полуинтервалы , количество элементов, попавших в каждый из них, математическое ожидание и дисперсия не изменятся.
Экспоненциальное
распределение
имеет
два независимых параметра:
и
.
;
Вычислим вероятности попадания в интервалы по формуле:
Результаты вычислений сведем в таблицу
Интервал |
|
[-3,665; -2,570] |
0,735 |
(-2,570; -2,039] |
0,126 |
(-2,039; -1,707] |
0,046 |
(-1,707; -1,503] |
0,021 |
(-1,503; -1,351] |
0,012 |
(-1,351; -1,170] |
0,012 |
(-1,170; -0,938] |
0,012 |
(-0,938; -0,708] |
0,008 |
(-0,708; -0,448] |
0,008 |
(-0,448; 0,719] |
0,015 |
Тогда
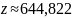
Так как вычисленное по выборке значение статистики не попадает в доверительную область, вычисленную ранее, то с вероятностью 0,95 можно утверждать, что данные выборки не согласуются с гипотезой о экспоненциальном распределении.
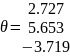
Т.к. заданный полином имеет четвертый порядок, то значение статистического показателя первой степени не попадает в полученные границы.